Difference between revisions of "Aufgaben:Exercise 1.4: Rayleigh PDF and Jakes PDS"
| Line 38: | Line 38: | ||
''Notes:'' | ''Notes:'' | ||
* This task belongs to the topic of [[Mobile_Communications/Statistical_bindings_within_the_Rayleigh_process|Statistical bindings within the Rayleigh process]]. | * This task belongs to the topic of [[Mobile_Communications/Statistical_bindings_within_the_Rayleigh_process|Statistical bindings within the Rayleigh process]]. | ||
| − | * To check your results you can use the interactive applet [[Applets:PDF,_CDF_and_Moments_of_Special_Distributions|PDF, CDF and Moments of Special Distributions]] | + | * To check your results you can use the interactive applet [[Applets:PDF,_CDF_and_Moments_of_Special_Distributions|PDF, CDF and Moments of Special Distributions]]. |
| Line 85: | Line 85: | ||
*By setting the derivative to $0$, you can show that the maximum of the PDF occurs at $a = \sigma$. Since the Rayleigh PDF applies to both channels, it follows that | *By setting the derivative to $0$, you can show that the maximum of the PDF occurs at $a = \sigma$. Since the Rayleigh PDF applies to both channels, it follows that | ||
| − | $$\sigma_{\rm R} = \sigma_{\rm B} \hspace{0.15cm} \underline{ = 1} \hspace{0.05cm}.$$ | + | :$$\sigma_{\rm R} = \sigma_{\rm B} \hspace{0.15cm} \underline{ = 1} \hspace{0.05cm}.$$ |
'''(2)''' As they fading coefficients have the same PDF, the desired probability is also the same for both channels. | '''(2)''' As they fading coefficients have the same PDF, the desired probability is also the same for both channels. | ||
*Using the given equation, we have | *Using the given equation, we have | ||
| − | $${\rm Pr}(a \le 0.316) = {\rm Pr}(20 \cdot {\rm lg}\hspace{0.15cm} a \le -10\,\,{\rm dB}) = 1 - {\rm e}^{ -{0.316^2}/(2\sigma^2)} | + | :$${\rm Pr}(a \le 0.316) = {\rm Pr}(20 \cdot {\rm lg}\hspace{0.15cm} a \le -10\,\,{\rm dB}) = 1 - {\rm e}^{ -{0.316^2}/(2\sigma^2)} |
= 1- 0.951 \hspace{0.15cm} \underline{ \approx 4.9 \%} | = 1- 0.951 \hspace{0.15cm} \underline{ \approx 4.9 \%} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 104: | Line 104: | ||
*The Rayleigh parameter $\sigma = 1$ also determines the „power” ${\rm E}[|z(t)|^2] = 2\sigma^2 = 2$ of the random process. | *The Rayleigh parameter $\sigma = 1$ also determines the „power” ${\rm E}[|z(t)|^2] = 2\sigma^2 = 2$ of the random process. | ||
*This applies to both '''R''' and '''B''': | *This applies to both '''R''' and '''B''': | ||
| − | $$\varphi_z ({\rm \delta}t = 0) = 2 \hspace{0.05cm}, \hspace{0.2cm} \int_{-\infty}^{+\infty}{\it \Phi}_z(f_{\rm D}) \hspace{0.15cm}{\rm d}f_{\rm D} = 2 \hspace{0.05cm}.$$ | + | :$$\varphi_z ({\rm \delta}t = 0) = 2 \hspace{0.05cm}, \hspace{0.2cm} \int_{-\infty}^{+\infty}{\it \Phi}_z(f_{\rm D}) \hspace{0.15cm}{\rm d}f_{\rm D} = 2 \hspace{0.05cm}.$$ |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 12:41, 11 August 2020
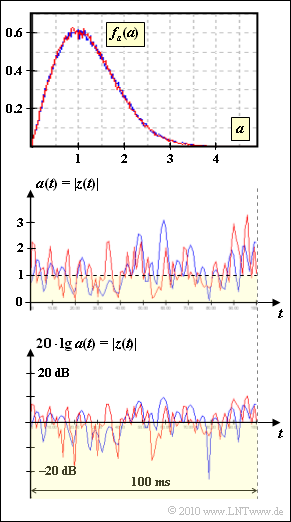
We consider two different mobile radio channels with Rayleigh fading. In both cases the PDF of the magnitude $a(t) = |z(t)| ≥ 0$ is
- $$f_a(a) = \frac{a}{\sigma^2} \cdot {\rm e}^{ -{a^2}/(2\sigma^2)} \hspace{0.05cm}.$$
The probability that this amount is not greater than a given value $A$ is
- $${\rm Pr}(|z(t)| \le A) = 1 - {\rm e}^{ -{A^2}/(2\sigma^2)} \hspace{0.05cm}.$$
The two channels, which are designated according to the colors „Red” and „Blue” in the graphs with $\rm R$ and $\rm B$ respectively, differ in the speed $v$ and thus in the form of the power spectral density (PSD) ${\it \Phi}_z(f_{\rm D})$.
- In both cases, however, the PSD is a Jakes spectrum.
- For a Doppler frequency $f_{\rm D}$ with $|f_{\rm D}| <f_{\rm D,\hspace{0.05cm}max}$ the Jakes spectrum is given by
- $${\it \pi}_z(f_{\rm D}) = \frac{1}{\pi \hspace{-0.05cm}\cdot \hspace{-0.05cm}f_{\rm D, \hspace{0.05cm} max} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\sqrt{ 1 \hspace{-0.05cm}- \hspace{-0.05cm}(f_{\rm D}/f_{\rm D, \hspace{0.05cm} max})^2} } \hspace{0.05cm}.$$
- For Doppler frequencies outside this interval from $-f_{\rm D,\hspace{0.05cm}max}$ to $+f_{\rm D,\hspace{0.05cm}max}$, we have ${\it \pi}_z(f_{\rm D})=0$.
The corresponding descriptor in the time domain is the autocorrelation function (ACF):
- $$\varphi_z ({\rm \delta}t) = 2 \sigma^2 \cdot {\rm J_0}(2\pi \cdot f_{\rm D, \hspace{0.05cm} max} \cdot {\rm \delta}t)\hspace{0.05cm}.$$
- Here, ${\rm J_0}(.)$ is the Bessel function of the first kind and zeroth order. We have ${\rm J_0}(0) = 1$.
- The maximum Doppler frequency of the channel model $\rm R$ : is known to be $f_{\rm D,\hspace{0.05cm}max} = 200 \ \rm Hz$.
- It is also known that the speeds $v_{\rm R}$ and $v_{\rm B}$ differ by the factor $2$ .
- Whether $v_{\rm R}$ is twice as large as $v_{\rm B}$ or vice versa, you should decide based on the above graphs.
Notes:
- This task belongs to the topic of Statistical bindings within the Rayleigh process.
- To check your results you can use the interactive applet PDF, CDF and Moments of Special Distributions.
Questionns
Solutions
- The Rayleigh PDF and its derivative are
- $$f_a(a) \hspace{-0.1cm} = \hspace{-0.1cm} \frac{a}{\sigma^2} \cdot {\rm e}^{ -a^2/(2\sigma^2)} \hspace{0.05cm},$$
- $$\frac{{\rm d}f_a(a)}{{\rm d}a} \hspace{-0.1cm} = \hspace{-0.1cm} \frac{1}{\sigma^2} \cdot {\rm e}^{ -a^2/(2\sigma^2)}- \frac{a^2}{\sigma^4} \cdot {\rm e}^{ -a^2/(2\sigma^2)} \hspace{0.05cm}.$$
- By setting the derivative to $0$, you can show that the maximum of the PDF occurs at $a = \sigma$. Since the Rayleigh PDF applies to both channels, it follows that
- $$\sigma_{\rm R} = \sigma_{\rm B} \hspace{0.15cm} \underline{ = 1} \hspace{0.05cm}.$$
(2) As they fading coefficients have the same PDF, the desired probability is also the same for both channels.
- Using the given equation, we have
- $${\rm Pr}(a \le 0.316) = {\rm Pr}(20 \cdot {\rm lg}\hspace{0.15cm} a \le -10\,\,{\rm dB}) = 1 - {\rm e}^{ -{0.316^2}/(2\sigma^2)} = 1- 0.951 \hspace{0.15cm} \underline{ \approx 4.9 \%} \hspace{0.05cm}.$$
(3) The correct solutions are 2, 3 and 6:
- The smaller speed $v_{\rm B}$ can be recognized by the fact that the magnitude $|z(t)|$ changes more slowly with the blue curve.
- When the vehicle is stationary, the PSD degenerates to ${\it \Phi_z}(f_{\rm D}) = 2\sigma^2\cdot \delta(f_{\rm D})$, and we have $|z(t)| = A = \rm const.$, where the constant $A$ is drawn from the Rayleigh distribution.
- At extremely high speed, the Jakes spectrum becomes flat and has an increasingly smaller magnitude over an increasingly wide range. It then approaches the PSD of white noise. However, $v$ would have to be in the order of the speed of light.
(4) Statements 2 and 3 are correct:
- The Rayleigh parameter $\sigma = 1$ also determines the „power” ${\rm E}[|z(t)|^2] = 2\sigma^2 = 2$ of the random process.
- This applies to both R and B:
- $$\varphi_z ({\rm \delta}t = 0) = 2 \hspace{0.05cm}, \hspace{0.2cm} \int_{-\infty}^{+\infty}{\it \Phi}_z(f_{\rm D}) \hspace{0.15cm}{\rm d}f_{\rm D} = 2 \hspace{0.05cm}.$$