Aufgaben:Exercise 2.1Z: Sum Signal

• Return to book

Rechtecksignal, Dreiecksignal und Summensignal

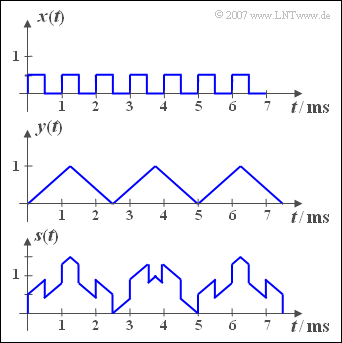
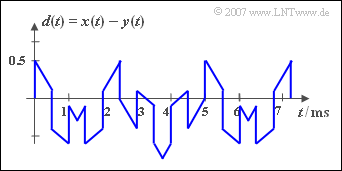
The adjacent diagram shows the two periodic signals  ${x(t)}$  and  ${y(t)}$ , from which the sum signal  ${s(t)}$  – sketched in the lower picture – and the difference signal  ${d(t)}$  are formed.

Furthermore, in this task we consider the signa  ${w(t)}$, which results from the sum of the two periodic signals  ${u(t)}$  und  $v(t)$ . The base frequencies of the signals are

• $f_u = 998 \,\text{Hz},$

• $f_v = 1002 \,\text{Hz}.$

That is all we know about the signals  ${u(t)}$  and  $v(t)$ .

Hinweis:

• Die Aufgabe gehört zum Kapitel  Allgemeine Beschreibung periodischer Signale.
• Mit dem interaktiven Applet  Periodendauer periodischer Signale  lässt sich die resultierende Periodendauer zweier harmonischer Schwingungen ermitteln.

Fragebogen

1

Wie groß ist Periodendauer  $T_x$  und Grundfrequenz  $f_x$  des Signals  ${x(t)}$?

$f_x\ = \ $   $\text{kHz}$

2

Wie groß ist Periodendauer  $T_y$  und Grundfrequenz  $f_y$  des Signals  ${y(t)}$?

$f_y\ = \ $   $\text{kHz}$

3

Bestimmen Sie die Grundfrequenz  $f_s$  sowie die Periodendauer  $T_s$  des Summensignals  ${s(t)}$  und überprüfen Sie das Ergebnis anhand der Skizze.

$T_s\ = \ $   $\text{ms}$

4

Welche Periodendauer  $T_d$  weist das Differenzsignal  ${d(t)}$  auf?

$T_d\ = \ $   $\text{ms}$

5

Welche Periodendauer  $T_w$  besitzt das Signal  ${w(t)} = {u(t)} + v(t)$?

$T_w\ = \ $   $\text{ms}$

Musterlösung

Solution

(1)  Für das Rechtecksignal gilt  $T_x = 1 \,\text{ms}$   ⇒   $f_x \hspace{0.15cm}\underline{= 1 \, \text{kHz}}$.

(2)  Für das Dreiecksignal gilt  $T_y = 2.5 \,\text{ms}$  und  $f_y \hspace{0.15cm}\underline{= 0.4\, \text{kHz}}$.

(3)  Die Grundfrequenz  $f_s$  des Summensignals  $s(t)$  ist der größte gemeinsame Teiler von  $f_x = 1 \,\text{kHz}$  und  $f_y = 0.4 \,\text{kHz}$.

• Daraus folgt  $f_s = 200 \,\text{Hz}$  und die Periodendauer  $T_s\hspace{0.15cm}\underline{ = 5 \,\text{ms}}$, wie auch aus der grafischen Darstellung des Signals  ${s(t)}$  auf der Angabenseite hervorgeht.

Differenzsignal $d(t) = x(t) - y(t)$

(4)  Die Periodendauer  $T_d$  ändert sich gegenüber der Periodendauer  $T_s$  nicht, wenn das Signal  ${y(t)}$  nicht addiert, sondern subtrahiert wird:     $T_d = T_s \hspace{0.15cm}\underline{= 5\, \text{ms}}$.

(5)  Der größte gemeinsame Teiler von  $f_u = 998 \,\text{Hz}$  und  $f_{v} = 1002 \,\text{Hz}$  ist  $f_w = 2 \,\text{Hz}$.

• Der Kehrwert hiervon ergibt die Periodendauer $T_w \hspace{0.15cm}\underline{= 500 \,\text{ms}}$.