Difference between revisions of "Aufgaben:Exercise 4.2: Rectangular Spectra"
m (Oezdemir moved page Aufgabe 4.2: Rechteckförmige Spektren to Exercise 4.2: Rectangular-Shaped Spectra) |
|||
| Line 4: | Line 4: | ||
[[File:P_ID695__Sig_A_4_2_neu.png|250px|right|frame|Rechteckförmige Tiefpass– und Bandpass–Spektren]] | [[File:P_ID695__Sig_A_4_2_neu.png|250px|right|frame|Rechteckförmige Tiefpass– und Bandpass–Spektren]] | ||
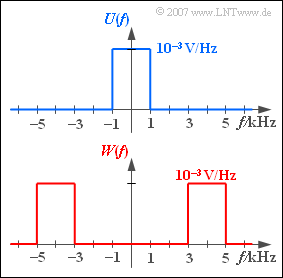
| − | + | We consider two signals $u(t)$ and $w(t)$ with rectangular spectra $U(f)$ and $W(f)$ respectively. | |
| − | * | + | *It is obvious that |
:$$u(t) = u_0 \cdot {\rm si} ( \pi \cdot {t}/{T_{ u}})$$ | :$$u(t) = u_0 \cdot {\rm si} ( \pi \cdot {t}/{T_{ u}})$$ | ||
| − | : | + | :is a low-pass signal whose two parameters $u_0$ and $T_u$ are to be determined in subtask '''(1)''' . |
| − | * | + | *In contrast, the spectrum $W(f)$ shows that $w(t)$ describes a bandpass signal. |
| − | + | This task also refers to the bandpass signal | |
:$$d(t) = 10 \hspace{0.05cm}{\rm V} \cdot {\rm si} ( 5 \pi f_2 \hspace{0.05cm}t) | :$$d(t) = 10 \hspace{0.05cm}{\rm V} \cdot {\rm si} ( 5 \pi f_2 \hspace{0.05cm}t) | ||
- 6 \hspace{0.05cm}{\rm V} \cdot {\rm si} ( 3 \pi f_2\hspace{0.05cm} t)$$ | - 6 \hspace{0.05cm}{\rm V} \cdot {\rm si} ( 3 \pi f_2\hspace{0.05cm} t)$$ | ||
| − | + | whose spectrum was determined in [[Aufgaben:Aufgabe_4.1:_Tiefpass-_und_Bandpass-Signale|task 4.1]] . Let $f_2 = 2 \ \rm kHz.$ | |
| Line 26: | Line 26: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *The task belongs to the chapter [[Signal_Representation/Differences_and_Similarities_of_LP_and_BP_Signals|Differences and Similarities of LP and BP Signals]]. |
| − | * | + | *Consider the following trigonometric relationship in the solution: |
:$$\sin (\alpha) \cdot \cos (\beta) = {1}/{2} \cdot \big[ \sin | :$$\sin (\alpha) \cdot \cos (\beta) = {1}/{2} \cdot \big[ \sin | ||
| Line 35: | Line 35: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the values of the parameters $u_0$ and $T_u$ of the low-pass signal? |
|type="{}"} | |type="{}"} | ||
$u_0\ = \ $ { 2 3% } $\text{V}$ | $u_0\ = \ $ { 2 3% } $\text{V}$ | ||
$T_u\ = \ $ { 0.5 3% } $\text{ms}$ | $T_u\ = \ $ { 0.5 3% } $\text{ms}$ | ||
| − | { | + | {Calculate the bandpass signal $w(t)$. What are the signal values at $t = 0$ and $t = 62.5 \, {\rm µ}\text{s}$? |
|type="{}"} | |type="{}"} | ||
$w(t=0)\ = \ $ { 4 3% } $\text{V}$ | $w(t=0)\ = \ $ { 4 3% } $\text{V}$ | ||
$w(t=62.5 \,{\rm µ} \text{s})\ = \ $ { 0. } $\text{V}$ | $w(t=62.5 \,{\rm µ} \text{s})\ = \ $ { 0. } $\text{V}$ | ||
| − | { | + | {Which statements are true regarding the bandpass signals $d(t)$ and $w(t)$ ? Justify your result in the time domain. |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The signals $d(t)$ and $w(t)$ are identical. |
| − | - $d(t)$ | + | - $d(t)$ and $w(t)$ differ by a constant factor. |
| − | - $d(t)$ und $w(t)$ | + | - $d(t)$ und $w(t)$ have different shapes. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The time $T_u$ ⇒ first zero of the LP signal $u(t)$ – is equal to the reciprocal of the width of the rectangular spectrum, i.e. $1/(2\, \text{kHz} ) \hspace{0.15 cm}\underline{= 0.5 \, \text{ms}}$. |
| − | * | + | *The pulse amplitude is equal to the rectangular area as shown in the sample solution for [[Aufgaben:Aufgabe_4.1:_Tiefpass-_und_Bandpass-Signale|task 4.1]] . From this follows $u_0\hspace{0.15 cm}\underline{= 2 \, \text{V}}$. |
Revision as of 19:46, 4 February 2021
We consider two signals $u(t)$ and $w(t)$ with rectangular spectra $U(f)$ and $W(f)$ respectively.
- It is obvious that
- $$u(t) = u_0 \cdot {\rm si} ( \pi \cdot {t}/{T_{ u}})$$
- is a low-pass signal whose two parameters $u_0$ and $T_u$ are to be determined in subtask (1) .
- In contrast, the spectrum $W(f)$ shows that $w(t)$ describes a bandpass signal.
This task also refers to the bandpass signal
- $$d(t) = 10 \hspace{0.05cm}{\rm V} \cdot {\rm si} ( 5 \pi f_2 \hspace{0.05cm}t) - 6 \hspace{0.05cm}{\rm V} \cdot {\rm si} ( 3 \pi f_2\hspace{0.05cm} t)$$
whose spectrum was determined in task 4.1 . Let $f_2 = 2 \ \rm kHz.$
Hints:
- The task belongs to the chapter Differences and Similarities of LP and BP Signals.
- Consider the following trigonometric relationship in the solution:
- $$\sin (\alpha) \cdot \cos (\beta) = {1}/{2} \cdot \big[ \sin (\alpha + \beta)+ \sin (\alpha - \beta)\big].$$
Questions
Solution
(1) The time $T_u$ ⇒ first zero of the LP signal $u(t)$ – is equal to the reciprocal of the width of the rectangular spectrum, i.e. $1/(2\, \text{kHz} ) \hspace{0.15 cm}\underline{= 0.5 \, \text{ms}}$.
- The pulse amplitude is equal to the rectangular area as shown in the sample solution for task 4.1 . From this follows $u_0\hspace{0.15 cm}\underline{= 2 \, \text{V}}$.
(2) Das Bandpass–Spektrum kann mit $f_{\rm T} = 4\, \text{kHz}$ wie folgt dargestellt werden:
- $$ W(f) = U(f- f_{\rm T}) + U(f+ f_{\rm T}) = U(f)\star \left[ \delta(f- f_{\rm T})+ \delta(f+ f_{\rm T})\right].$$
Entsprechend dem Verschiebungssatz gilt dann für das dazugehörige Zeitsignal:
- $$w(t) = 2 \cdot u(t) \cdot {\cos} ( 2 \pi f_{\rm T} t) = 2 u_0 \cdot {\rm si} ( \pi {t}/{T_{\rm u}})\cdot {\cos} ( 2 \pi f_{\rm T} t). $$
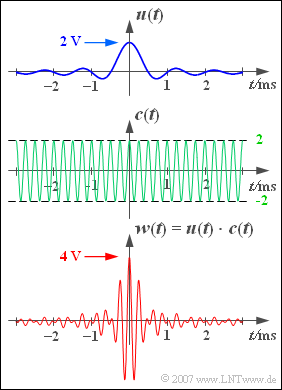
Die Grafik zeigt
- oben das Tiefpass–Signal $u(t)$,
- dann die Schwingung $c(t) = 2 · \cos(2 \pi fTt$ ),
- unten das Bandpass–Signal $w(t) = u(t) \cdot c(t)$.
Insbesondere erhält man zum Zeitpunkt $t = 0$:
- $$w(t = 0) = 2 \cdot u_0 \hspace{0.15 cm}\underline{= 4 \hspace{0.05cm}{\rm V}}.$$
Der Zeitpunkt $t=62.5 \,{\rm µ} \text{s}$ entspricht genau einer viertel Periodendauer des Signals $c(t)$:
- $$ w(t = 62.5 \hspace{0.05cm}{\rm µ s}) = 2 u_0 \cdot {\rm si} ( \pi \cdot \frac{62.5 \hspace{0.05cm}{\rm µ s}} {500 \hspace{0.05cm}{\rm µ s}}) \cdot {\cos} ( 2 \pi \cdot 4\hspace{0.05cm}{\rm kHz}\cdot 62.5 \hspace{0.05cm}{\rm µ s}) $$
- $$ \Rightarrow \hspace{0.3cm}w(t = 4\hspace{0.05cm}{\rm V}\cdot{\rm si} ( {\pi}/{8}) \cdot \cos ( {\pi}/{4})\hspace{0.15 cm}\underline{ = 0}.$$
(3) Richtig ist der Lösungsvorschlag 1:
- Vergleicht man die Spektralfunktion $W(f)$ dieser Aufgabe mit dem Spektrum $D(f)$ in der Musterlösung zu Aufgabe 4.1, so erkennt man, dass $w(t)$ und $d(t)$ identische Signale sind.
- Etwas aufwändiger ist dieser Beweis im Zeitbereich. Mit $f_2 = 2 \,\text{kHz}$ kann für das hier betrachtete Signal geschrieben werden:
- $$w(t ) = 4\hspace{0.05cm}{\rm V} \cdot {\rm si} ( \pi f_2 t) \cdot {\cos} ( 4 \pi f_2 t) = ({4\hspace{0.05cm}{\rm V}})/({\pi f_2 t})\cdot \sin (\pi f_2 t) \cdot \cos ( 4 \pi f_2 t) .$$
- Wegen der trigonometrischen Beziehung
- $$\sin (\alpha) \cdot \cos (\beta) = {1}/{2} \cdot \big[ \sin (\alpha + \beta)+ \sin (\alpha - \beta)\big]$$
- kann obige Gleichung umgeformt werden:
- $$w(t ) = \frac{2\hspace{0.05cm}{\rm V}}{\pi f_2 t}\cdot \big [\sin (5\pi f_2 t) + \sin (-3\pi f_2 t)\big ] = 10\hspace{0.05cm}{\rm V} \cdot \frac{\sin (5\pi f_2 t)}{5\pi f_2 t}- 6\hspace{0.05cm}{\rm V} \cdot \frac{\sin (3\pi f_2 t)}{3\pi f_2 t}.$$
- Damit ist gezeigt, dass beide Signale tatsächlich identisch sind ⇒ Lösungsvorschlag 1:
- $$w(t) = 10 \hspace{0.05cm}{\rm V} \cdot {\rm si} ( 5 \pi f_2 t) - 6 \hspace{0.05cm}{\rm V} \cdot {\rm si} ( 3 \pi f_2 t) = d(t).$$