Difference between revisions of "Signal Representation/Analytical Signal and its Spectral Function"
| Line 43: | Line 43: | ||
| − | == | + | ==Calculation Procedure in The Time Domain== |
<br> | <br> | ||
[[File:Sig_T_4_2_S2a_Version2.png|right|frame|To Derive the Analytical Signal]] | [[File:Sig_T_4_2_S2a_Version2.png|right|frame|To Derive the Analytical Signal]] | ||
| Line 51: | Line 51: | ||
If one considers the nbsp; [[Signal_Representation/Fourier_Transform_Laws#Zuordnungssatz|Mapping Theorem]] of the Fourier transform, then the following statements are possible on the basis of the graphic: | If one considers the nbsp; [[Signal_Representation/Fourier_Transform_Laws#Zuordnungssatz|Mapping Theorem]] of the Fourier transform, then the following statements are possible on the basis of the graphic: | ||
| − | * | + | *The even part $X_{\rm +g}(f)$ of $X_{+}(f)$ leads after the Fourier transformation to a real time signal, the odd part $X_{\rm +u}(f)$ to an imaginary one. |
| − | * | + | *It is obvious that $X_{\rm +g}(f)$ is equal to the actual Fourier spectrum $X(f)$ and thus the real part of $x_{\rm +g}(t)$ is equal to the given signal $x(t)$ with bandpass properties. |
| − | * | + | *If we denote the imaginary part with $y(t)$, the analytical signal is: |
:$$x_+(t)= x(t) + {\rm j} \cdot y(t) .$$ | :$$x_+(t)= x(t) + {\rm j} \cdot y(t) .$$ | ||
| − | * | + | *According to the generally valid laws of Fourier transform corresponding to the [[Signal_Representation/Fourier_Transform_Laws#Zuordnungssatz|Mapping Theorem]] , the following applies to the spectral function of the imaginary part: |
:$${\rm j} \cdot Y(f) = X_{\rm +u}(f)= {\rm sign}(f) \cdot X(f) | :$${\rm j} \cdot Y(f) = X_{\rm +u}(f)= {\rm sign}(f) \cdot X(f) | ||
\hspace{0.3cm}\Rightarrow\hspace{0.3cm}Y(f) = \frac{{\rm | \hspace{0.3cm}\Rightarrow\hspace{0.3cm}Y(f) = \frac{{\rm | ||
sign}(f)}{ {\rm j}}\cdot X(f).$$ | sign}(f)}{ {\rm j}}\cdot X(f).$$ | ||
| − | * | + | *If one transforms this equation into the time domain, the multiplication becomes the [[Signal_Representation/The_Convolution_Theorem_and_Operation|convolution]], and one gets: |
:$$y(t) = \frac{1}{ {\rm \pi} t} \hspace{0.05cm}\star | :$$y(t) = \frac{1}{ {\rm \pi} t} \hspace{0.05cm}\star | ||
\hspace{0.05cm}x(t) = \frac{1}{ {\rm \pi}} \cdot | \hspace{0.05cm}x(t) = \frac{1}{ {\rm \pi}} \cdot | ||
| Line 65: | Line 65: | ||
\tau}}\hspace{0.15cm} {\rm d}\tau.$$ | \tau}}\hspace{0.15cm} {\rm d}\tau.$$ | ||
| − | == | + | ==Representation with Hilbert Transform== |
<br> | <br> | ||
| − | + | At this point it is necessary to briefly discuss a further spectral transformation, which is dealt thoroughly in the book [[Linear_and_Time_Invariant_Systems/Folgerungen_aus_dem_Zuordnungssatz#Hilbert.E2.80.93Transformation|Linear and Time Invariant Systems Systeme]] . | |
| − | |||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ FFor the '''Hilbert transformed''' $ {\rm H}\left\{x(t)\right\}$ a time function $x(t)$ applies: |
:$$y(t) = {\rm H}\left\{x(t)\right\} = \frac{1}{ {\rm \pi} } \cdot | :$$y(t) = {\rm H}\left\{x(t)\right\} = \frac{1}{ {\rm \pi} } \cdot | ||
| Line 76: | Line 75: | ||
\tau} }\hspace{0.15cm} {\rm d}\tau.$$ | \tau} }\hspace{0.15cm} {\rm d}\tau.$$ | ||
| − | * | + | *This particular integral cannot be solved in a simple, conventional way, but must be evaluated using the [https://en.wikipedia.org/wiki/Cauchy_principal_value principal value of Cauchy] . |
| − | * | + | *Correspondingly valid in the frequency domain: |
:$$Y(f) = - {\rm j} \cdot {\rm sign}(f) \cdot X(f) \hspace{0.05cm} .$$}} | :$$Y(f) = - {\rm j} \cdot {\rm sign}(f) \cdot X(f) \hspace{0.05cm} .$$}} | ||
| − | + | The result of the last page can be summarized with this definition as follows: | |
| − | * | + | *You get from the real, physical bandpass signal $x(t)$ the analytic signal $x_+(t)$ by adding to $x(t)$ an imaginary part according to the Hilbert transform: |
:$$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$ | :$$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$ | ||
| − | * | + | *The Hilbert transformed $\text{H}\{x(t)\}$ disappears only in the case of $x(t) = \rm const.$ ⇒ DC signal With all other signal forms the analytic signal $x_+(t)$ is therefore always complex. |
| − | * | + | *From the analytical signal $x_+(t)$ the real bandpass signal can be easily determined by real part formation: |
:$$x(t) = {\rm Re}\left\{x_+(t)\right\} .$$ | :$$x(t) = {\rm Re}\left\{x_+(t)\right\} .$$ | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 2:}$ The principle of the Hilbert transformation is illustrated again by the following diagram: |
| − | * | + | **According to the left representation $\rm (A)$ ,one gets an analytical signal $x_+(t)$ from the physical signal $x(t)$ by adding an imaginary part ${\rm j} \cdot y(t)$ . |
| − | * | + | *Here $y(t) = {\rm H}\left\{x(t)\right\}$ is a real time function, which can be calculated easily in the spectral range by multiplying the spectrum $X(f)$ with $- {\rm j} \cdot \sign(f)$ . |
| − | [[File:P_ID2729__Sig_T_4_2_S2b_neu.png|center|frame| | + | [[File:P_ID2729__Sig_T_4_2_S2b_neu.png|center|frame|On the Illustration of the Hilbert Transformed]] |
| − | + | The right representation $\rm (B)$ is equivalent to $\rm (A)$: | |
| − | * | + | *Now applies $x_+(t) = x(t) + z(t)$ with the purely imaginary function $z(t)$. |
| − | * | + | *A comparison of the two images shows that actually $z(t) = {\rm j} \cdot y(t)$ is valid.} |
| − | == | + | ==Vector Diagram Representation of The Harmonic Oscillation== |
<br> | <br> | ||
| − | + | The spectral function $X(f)$ of a harmonic oscillation $x(t) = A \cdot \text{cos}(2\pi f_{\rm T}t - \varphi)$ consists of two Dirac functions at the frequencies | |
| − | * $+f_{\rm T}$ | + | * $+f_{\rm T}$ with the complex weight $A/2 \cdot \text{e}^{-\text{j}\hspace{0.05cm}\varphi}$, |
| − | * $-f_{\rm T}$ | + | * $-f_{\rm T}$ with the complex weight $A/2 \cdot \text{e}^{+\text{j}\hspace{0.05cm}\varphi}$. |
| − | + | Thus, the spectrum of the analytical signal is $($without the Dirac function at the frequency $f =-f_{\rm T})$: | |
:$$X_+(f) = A \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\varphi}\cdot\delta (f - f_{\rm | :$$X_+(f) = A \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\varphi}\cdot\delta (f - f_{\rm | ||
T}) .$$ | T}) .$$ | ||
| − | + | The corresponding time function is obtained by applying the [[Signal_Representation/Fourier_Transform_Laws#Verschiebungssatz|Shifting Theorem]]: | |
:$$x_+(t) = A \cdot {\rm e}^{\hspace{0.05cm} {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}( 2 \pi f_{\rm T} t | :$$x_+(t) = A \cdot {\rm e}^{\hspace{0.05cm} {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}( 2 \pi f_{\rm T} t | ||
\hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$ | \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$ | ||
| − | + | This equation describes a rotating pointer with constant angular velocity $\omega_{\rm T} = 2\pi f_{\rm T}$ . | |
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
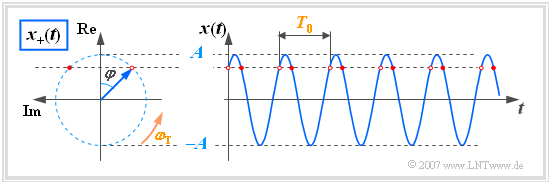
| − | $\text{ | + | $\text{Example 3:}$ For illustrative reasons the coordinate system in the following figure is rotated to the left (real part up, imaginary part to the left), contrary to the usual representation by $90^\circ$ . |
| − | [[File:P_ID712__Sig_T_4_2_S3.png|center|frame| | + | [[File:P_ID712__Sig_T_4_2_S3.png|center|frame|Vector Diagram of a Harmonic Oscillation]] |
Anhand dieser Grafik sind folgende Aussagen möglich: | Anhand dieser Grafik sind folgende Aussagen möglich: | ||
| − | * | + | On the basis of this diagram the following statements are possible: |
| − | * | + | *At the start time $t = 0$ the pointer of length $A$ (signal amplitude) lies with angle $-\varphi$ in the complex plane. In the drawn example, $\varphi = 45^\circ$. |
| − | * | + | *For the times $t > 0$ the pointer rotates with constant angular velocity (angular frequency) $\omega_{\rm T}$ in mathematically positive direction, i.e. counterclockwise. |
| − | * | + | *The top of the pointer thus always lies on a circle with radius $A$ and requires exactly the time $T_0$, i.e. the period of the harmonic oscillation $x(t)$ for one rotation. |
| + | *The projection of the analytical signal $x_+(t)$ onto the real axis, marked by red dots, provides the instantaneous values of $x(t)$.}} | ||
| − | == | + | ==Vector Diagram of a Sum of Harmonic Oscillations== |
<br> | <br> | ||
| − | + | For further description we assume the following spectrum for the analytical signal: | |
:$$X_+(f) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} | :$$X_+(f) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} | ||
\varphi_i}\cdot\delta (f - f_{i}) .$$ | \varphi_i}\cdot\delta (f - f_{i}) .$$ | ||
| − | + | The left image shows such a spectrum for the example $I = 3$. If one chooses $I$ relatively large and the distance between adjacent spectral lines correspondingly small, then (frequency–) continuous spectral functions $X_+(f)$ can also be approximated with the above equation. | |
| − | [[File:P_ID715__Sig_T_4_2_S4.png|center|frame| | + | [[File:P_ID715__Sig_T_4_2_S4.png|center|frame|Vector Diagram of a Sum of 3 Oscillations]] |
| − | + | In the right picture the corresponding time function is indicated. This is in general: | |
:$$x_+(t) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}(\omega_i | :$$x_+(t) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}(\omega_i | ||
\hspace{0.05cm}\cdot\hspace{0.05cm} t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$ | \hspace{0.05cm}\cdot\hspace{0.05cm} t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$ | ||
| − | + | To note about this graphic: | |
| − | * | + | *The sketch shows the initial position of the pointers at the start time $t = 0$ corresponding to the amplitudes $A_i$ and the phase positions $\varphi_i$. |
| − | * | + | *The tip of the resulting pointer compound is marked by the violet cross. One obtains by vectorial addition of the three individual pointers for the time $t = 0$: |
:$$x_+(t= 0) = \big [1 \cdot \cos(60^\circ) - 1 \cdot {\rm j} \cdot \sin(60^\circ) \big ]+ 2 \cdot \cos(0^\circ)+1 \cdot \cos(180^\circ) = 1.500 - {\rm j} \cdot 0.866.$$ | :$$x_+(t= 0) = \big [1 \cdot \cos(60^\circ) - 1 \cdot {\rm j} \cdot \sin(60^\circ) \big ]+ 2 \cdot \cos(0^\circ)+1 \cdot \cos(180^\circ) = 1.500 - {\rm j} \cdot 0.866.$$ | ||
| − | * | + | *For times $t > 0$ the three pointers rotate at different angular speeds $\omega_i = 2\pi f_i$. The red hand rotates faster than the green hand, but slower than the blue hand. |
| − | * | + | *Since all hands rotate counterclockwise, the resulting hand $x_+(t)$ will also tend to move in this direction. At time $t = 1\,µ\text {s}$ the peak of the resulting pointer for the given parameter values is |
| + | |||
:$$ \begin{align*}x_+(t = 1 {\rm \hspace{0.05cm}µ s}) & = 1 \cdot {\rm e}^{-{\rm | :$$ \begin{align*}x_+(t = 1 {\rm \hspace{0.05cm}µ s}) & = 1 \cdot {\rm e}^{-{\rm | ||
j}\hspace{0.05cm}\cdot \hspace{0.05cm}60^\circ}\cdot {\rm e}^{{\rm | j}\hspace{0.05cm}\cdot \hspace{0.05cm}60^\circ}\cdot {\rm e}^{{\rm | ||
| Line 171: | Line 171: | ||
e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}21.6^\circ} \approx | e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}21.6^\circ} \approx | ||
1.673- {\rm j} \cdot 0.464.\end{align*}$$ | 1.673- {\rm j} \cdot 0.464.\end{align*}$$ | ||
| − | * | + | *The resulting pointer tip does not lie on a circle like a single oscillation, but a complicated geometric figure is created. |
| − | |||
| − | |||
| + | The interactive applet [[Applets:Physikalisches_Signal_%26_Analytisches_Signal|Physical Signal & Analytical Signal]] illustrates $x_+(t)$ for the sum of three harmonic oscillations. | ||
| − | == | + | ==Exercises for the Chapter== |
<br> | <br> | ||
[[Aufgaben:Exercise 4.3: Vector Diagram Representation|Exercise 4.3: Vector Diagram Representation]] | [[Aufgaben:Exercise 4.3: Vector Diagram Representation|Exercise 4.3: Vector Diagram Representation]] | ||
Revision as of 16:11, 26 November 2020
Contents
Definition in the Frequency Domain
We consider a real bandpass-like signal $x(t)$ with the corresponding bandpass spectrum $X(f)$, which has an even real and an odd imaginary part with respect to the frequency zero point. It is assumed that the carrier frequency $f_{\rm T}$ is much larger than the bandwidth of the bandpass signal $x(t)$ .
$\text{Definition:}$ The time function belonging to the physical signal $x(t)$ analytical signal $x_+(t)$ is that time function, whose spectrum fulfills the following property
- $$X_+(f)=\big[1+{\rm sign}(f)\big] \cdot X(f) = \left\{ {2 \cdot X(f) \; \hspace{0.2cm}\rm for\hspace{0.2cm} {\it f} > 0, \atop {\,\,\,\, \rm 0 \; \hspace{0.9cm}\rm for\hspace{0.2cm} {\it f} < 0.} }\right.$$
The so called „signum function” is for positive values of $f$ equal to $+1$ and for negative $f$-values equal to $-1$.
- The (double sided) limit value returns $\sign(0) = 0$.
- The index "+" should make clear that $X_+(f)$ has only parts at positive frequencies.
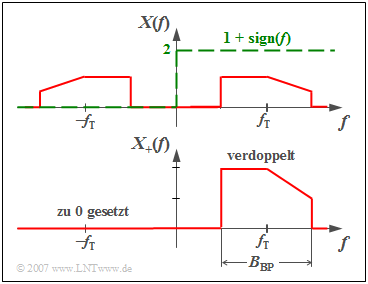
From the graphic you can see the calculation rule for $X_+(f)$:
The actual bandpass spectrum $X(f)$ will
- doubled at the positive frequencies, and
- set to zero at the negative frequencies.
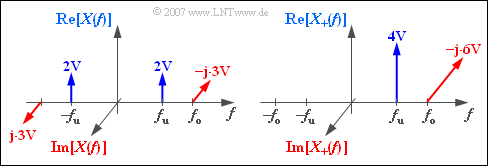
$\text{Example 1:}$
The graphic
- at left shows the (complex) spectrum $X(f)$ of the bandpass signal
- $$x(t) = 4\hspace{0.05cm}{\rm V} \cdot {\cos} ( 2 \pi f_{\rm u} \hspace{0.03cm}t) + 6\hspace{0.05cm}{\rm V} \cdot {\sin} ( 2 \pi f_{\rm o} \hspace{0.03cm}t).$$
- and on the right the (complex) spectrum of the analytical signal $x_{+}(t)$.
Calculation Procedure in The Time Domain
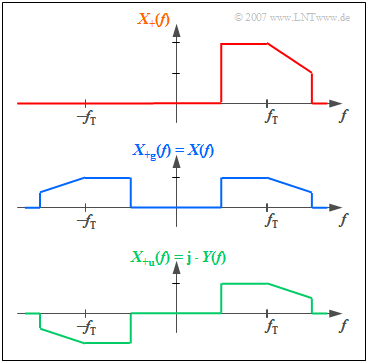
Now we will take a closer look at the spectrum $X_+(f)$ of the analytical signal and divide it into a with respect to $f = 0$ even part $X_{\rm +g}(f)$ and an odd part $X_{\rm +u}(f)$ :
- $$X_+(f) = X_{\rm +g}(f) + X_{\rm +u}(f).$$
All these spectra are generally complex.
If one considers the nbsp; Mapping Theorem of the Fourier transform, then the following statements are possible on the basis of the graphic:
- The even part $X_{\rm +g}(f)$ of $X_{+}(f)$ leads after the Fourier transformation to a real time signal, the odd part $X_{\rm +u}(f)$ to an imaginary one.
- It is obvious that $X_{\rm +g}(f)$ is equal to the actual Fourier spectrum $X(f)$ and thus the real part of $x_{\rm +g}(t)$ is equal to the given signal $x(t)$ with bandpass properties.
- If we denote the imaginary part with $y(t)$, the analytical signal is:
- $$x_+(t)= x(t) + {\rm j} \cdot y(t) .$$
- According to the generally valid laws of Fourier transform corresponding to the Mapping Theorem , the following applies to the spectral function of the imaginary part:
- $${\rm j} \cdot Y(f) = X_{\rm +u}(f)= {\rm sign}(f) \cdot X(f) \hspace{0.3cm}\Rightarrow\hspace{0.3cm}Y(f) = \frac{{\rm sign}(f)}{ {\rm j}}\cdot X(f).$$
- If one transforms this equation into the time domain, the multiplication becomes the convolution, and one gets:
- $$y(t) = \frac{1}{ {\rm \pi} t} \hspace{0.05cm}\star \hspace{0.05cm}x(t) = \frac{1}{ {\rm \pi}} \cdot \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - \tau}}\hspace{0.15cm} {\rm d}\tau.$$
Representation with Hilbert Transform
At this point it is necessary to briefly discuss a further spectral transformation, which is dealt thoroughly in the book Linear and Time Invariant Systems Systeme .
$\text{Definition:}$ FFor the Hilbert transformed $ {\rm H}\left\{x(t)\right\}$ a time function $x(t)$ applies:
- $$y(t) = {\rm H}\left\{x(t)\right\} = \frac{1}{ {\rm \pi} } \cdot \hspace{0.03cm}\int_{-\infty}^{+\infty}\frac{x(\tau)}{ {t - \tau} }\hspace{0.15cm} {\rm d}\tau.$$
- This particular integral cannot be solved in a simple, conventional way, but must be evaluated using the principal value of Cauchy .
- Correspondingly valid in the frequency domain:
- $$Y(f) = - {\rm j} \cdot {\rm sign}(f) \cdot X(f) \hspace{0.05cm} .$$
The result of the last page can be summarized with this definition as follows:
- You get from the real, physical bandpass signal $x(t)$ the analytic signal $x_+(t)$ by adding to $x(t)$ an imaginary part according to the Hilbert transform:
- $$x_+(t) = x(t)+{\rm j} \cdot {\rm H}\left\{x(t)\right\} .$$
- The Hilbert transformed $\text{H}\{x(t)\}$ disappears only in the case of $x(t) = \rm const.$ ⇒ DC signal With all other signal forms the analytic signal $x_+(t)$ is therefore always complex.
- From the analytical signal $x_+(t)$ the real bandpass signal can be easily determined by real part formation:
- $$x(t) = {\rm Re}\left\{x_+(t)\right\} .$$
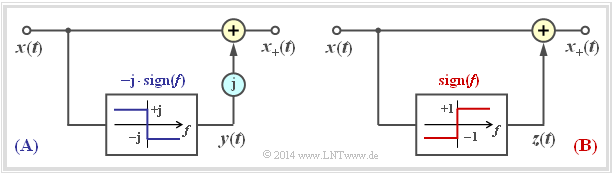
{{GraueBox|TEXT= $\text{Example 2:}$ The principle of the Hilbert transformation is illustrated again by the following diagram:
- According to the left representation $\rm (A)$ ,one gets an analytical signal $x_+(t)$ from the physical signal $x(t)$ by adding an imaginary part ${\rm j} \cdot y(t)$ .
- Here $y(t) = {\rm H}\left\{x(t)\right\}$ is a real time function, which can be calculated easily in the spectral range by multiplying the spectrum $X(f)$ with $- {\rm j} \cdot \sign(f)$ .
The right representation $\rm (B)$ is equivalent to $\rm (A)$:
- Now applies $x_+(t) = x(t) + z(t)$ with the purely imaginary function $z(t)$.
- A comparison of the two images shows that actually $z(t) = {\rm j} \cdot y(t)$ is valid.}
Vector Diagram Representation of The Harmonic Oscillation
The spectral function $X(f)$ of a harmonic oscillation $x(t) = A \cdot \text{cos}(2\pi f_{\rm T}t - \varphi)$ consists of two Dirac functions at the frequencies
- $+f_{\rm T}$ with the complex weight $A/2 \cdot \text{e}^{-\text{j}\hspace{0.05cm}\varphi}$,
- $-f_{\rm T}$ with the complex weight $A/2 \cdot \text{e}^{+\text{j}\hspace{0.05cm}\varphi}$.
Thus, the spectrum of the analytical signal is $($without the Dirac function at the frequency $f =-f_{\rm T})$:
- $$X_+(f) = A \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\varphi}\cdot\delta (f - f_{\rm T}) .$$
The corresponding time function is obtained by applying the Shifting Theorem:
- $$x_+(t) = A \cdot {\rm e}^{\hspace{0.05cm} {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}( 2 \pi f_{\rm T} t \hspace{0.05cm}-\hspace{0.05cm} \varphi)}.$$
This equation describes a rotating pointer with constant angular velocity $\omega_{\rm T} = 2\pi f_{\rm T}$ .
$\text{Example 3:}$ For illustrative reasons the coordinate system in the following figure is rotated to the left (real part up, imaginary part to the left), contrary to the usual representation by $90^\circ$ .
Anhand dieser Grafik sind folgende Aussagen möglich: On the basis of this diagram the following statements are possible:
- At the start time $t = 0$ the pointer of length $A$ (signal amplitude) lies with angle $-\varphi$ in the complex plane. In the drawn example, $\varphi = 45^\circ$.
- For the times $t > 0$ the pointer rotates with constant angular velocity (angular frequency) $\omega_{\rm T}$ in mathematically positive direction, i.e. counterclockwise.
- The top of the pointer thus always lies on a circle with radius $A$ and requires exactly the time $T_0$, i.e. the period of the harmonic oscillation $x(t)$ for one rotation.
- The projection of the analytical signal $x_+(t)$ onto the real axis, marked by red dots, provides the instantaneous values of $x(t)$.
Vector Diagram of a Sum of Harmonic Oscillations
For further description we assume the following spectrum for the analytical signal:
- $$X_+(f) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} \varphi_i}\cdot\delta (f - f_{i}) .$$
The left image shows such a spectrum for the example $I = 3$. If one chooses $I$ relatively large and the distance between adjacent spectral lines correspondingly small, then (frequency–) continuous spectral functions $X_+(f)$ can also be approximated with the above equation.
In the right picture the corresponding time function is indicated. This is in general:
- $$x_+(t) = \sum_{i=1}^{I}A_i \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}(\omega_i \hspace{0.05cm}\cdot\hspace{0.05cm} t \hspace{0.05cm}-\hspace{0.05cm} \varphi_i)}.$$
To note about this graphic:
- The sketch shows the initial position of the pointers at the start time $t = 0$ corresponding to the amplitudes $A_i$ and the phase positions $\varphi_i$.
- The tip of the resulting pointer compound is marked by the violet cross. One obtains by vectorial addition of the three individual pointers for the time $t = 0$:
- $$x_+(t= 0) = \big [1 \cdot \cos(60^\circ) - 1 \cdot {\rm j} \cdot \sin(60^\circ) \big ]+ 2 \cdot \cos(0^\circ)+1 \cdot \cos(180^\circ) = 1.500 - {\rm j} \cdot 0.866.$$
- For times $t > 0$ the three pointers rotate at different angular speeds $\omega_i = 2\pi f_i$. The red hand rotates faster than the green hand, but slower than the blue hand.
- Since all hands rotate counterclockwise, the resulting hand $x_+(t)$ will also tend to move in this direction. At time $t = 1\,µ\text {s}$ the peak of the resulting pointer for the given parameter values is
- $$ \begin{align*}x_+(t = 1 {\rm \hspace{0.05cm}µ s}) & = 1 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}60^\circ}\cdot {\rm e}^{{\rm j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}40 \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001} + 2\cdot {\rm e}^{{\rm j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}50 \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001}- 1\cdot {\rm e}^{{\rm j}\hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.1cm}60 \hspace{0.05cm} \cdot \hspace{0.1cm} 0.001} = \\ & = 1 \cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}45.6^\circ} + 2\cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}18^\circ}- 1\cdot {\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}21.6^\circ} \approx 1.673- {\rm j} \cdot 0.464.\end{align*}$$
- The resulting pointer tip does not lie on a circle like a single oscillation, but a complicated geometric figure is created.
The interactive applet Physical Signal & Analytical Signal illustrates $x_+(t)$ for the sum of three harmonic oscillations.
Exercises for the Chapter
Exercise 4.3: Vector Diagram Representation
Exercise 4.3Z: Hilbert Transformator
Exercise 4.4: Vector Diagram for DSB-AM
Exercise 4.4Z: Vector Diagram for DSB-AM