Aufgaben:Exercise 2.2: DC Component of Signals

• Return to book

Rechtecksignale mit und ohne Gleichanteil

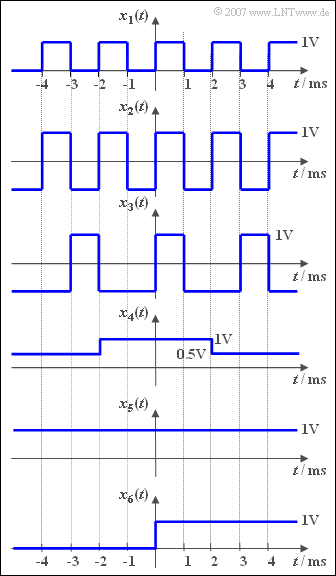
The graph shows some time signals defined for all times $($from  $-\infty$  to  $+\infty)$ . For all six sample signals  $x_i(t)$  the associated spectral function can be written as:

$$X_i(f)=A_0\cdot{\rm \delta}(f)+\Delta X_i(f).$$

Here

• $A_0$  is the DC component, and
• $\Delta X_i(f)$  is the spectrum of the residual signal reduced by the DC component  $\Delta x_i(t) = x_i(t) - A_0$.

Hint:

• This exercise belongs to the chapter  Direct Current Signal - Limit Case of a Periodic Signal.

Questions

1

Welche der Signale beinhalten einen Gleichanteil, das heißt, bei welchen Signalen ist  $A_0 \neq 0$?

	Signal  $x_1(t),$
	Signal  $x_2(t),$
	Signal  $x_3(t),$
	Signal  $x_4(t),$
	Signal  $x_5(t),$
	Signal  $x_6(t).$

2

Bei welchen der Signale gilt für das „Restspektrum”  $\Delta X_i(f) =0$?

	Signal  $x_1(t),$
	Signal  $x_2(t),$
	Signal  $x_3(t),$
	Signal  $x_4(t),$
	Signal  $x_5(t),$
	Signal  $x_6(t).$

3

Wie groß ist der Gleichanteil des Signals  $x_3(t)$?

$x_3(t)\hspace{-0.1cm}:\,\,A_0 \ = \ $   ${\rm V}$

4

Wie groß ist der Gleichanteil des Signals  $x_4(t)$?

$x_4(t)\hspace{-0.1cm}:\,\,A_0\ = \ $   ${\rm V}$

5

Wie groß ist der Gleichanteil des Signals  $x_6(t)$?

$x_6(t)\hspace{-0.1cm}:\,\,A_0\ = \ $   ${\rm V}$

Musterlösung

Solution

(1)  Richtig sind die Antworten 1, 3, 4, 5 und 6.

• Alle Signale mit Ausnahme von  $x_2(t)$  beinhalten einen Gleichsignalanteil.

(2)  Richtig ist allein der Lösungsvorschlag 5:

• Subtrahiert man vom Signal  $x_5(t)$  den Gleichanteil  $1\text{V}$, so ist das Restsignal  $\Delta x_5(t) = x5(t) - 1\text{V}$  gleich Null.
• Dementspechend ist auch die Spektralfunktion  $\Delta X_5(f) = 0$.
• Bei allen anderen Zeitverläufen ist  $\Delta x_i(t)$  ungleich Null und damit auch die dazugehörige Spektralfunktion  $\Delta X_i(f)$.

(3)  Bei einem periodischen Signal genügt zur Berechnung des Gleichsignalanteils  $A_0$  die Mittelung über eine Periodendauer.

• Beim Beispielsignal  $x_3(t)$  ist diese  $T_0 = 3\,\text{ms}$. Damit ergibt sich der gesuchte Gleichanteil zu

$$A_0=\rm \frac{1}{3\,ms}\cdot \big[1\,V\cdot 1\,ms+(-1\,V)\cdot 2\,ms \big] \hspace{0.15cm}\underline{=-0.333\,V}.$$

(4)  Für das Signal  $x_4(t)$  kann geschrieben werden:  $x_4(t) = 0.5 \,{\rm V} + Δx_4(t)$.

• Hierbei bezeichnet  $Δx_4(t)$  einen Rechteckimpuls mit Amplitude  $0.5 \,{\rm V}$  und Dauer  $4 \,{\rm ms}$, der wegen seiner endlichen Dauer nicht zum Gleichsignalanteil beiträgt.
• Deshalb gilt hier  $A_0 \hspace{0.15cm}\underline{=0.5 \,{\rm V}}$.

(5)  Die allgemeine Gleichung zur Berechnung des Gleichsignalanteils lautet:

$$A_0=\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int_{-T_{\rm M}/2}^{+T_{\rm M}/2}x(t)\, {\rm d }t.$$

• Spaltet man dieses Integral in zwei Teilintegrale auf, so erhält man:

$$A_0=\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int _{-T_{\rm M}/2}^{0}0 {\rm V} \cdot\, {\rm d } {\it t }+\lim_{T_{\rm M}\to \infty}\frac{1}{T_{\rm M}}\int _{0}^{+T_{\rm M}/2}1 \rm V \ {\rm d }{\it t }.$$

• Nur der zweite Term liefert einen Beitrag. Daraus folgt wiederum  $A_0 \hspace{0.15cm}\underline{=0.5 \,{\rm V}}$.