Difference between revisions of "Aufgaben:Exercise 3.2Z: Sinc-Squared Spectrum with Diracs"
| Line 60: | Line 60: | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
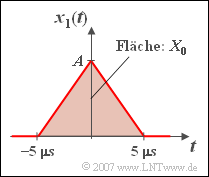
[[File:P_ID498__Sig_Z_3_2_a_neu.png|right|frame|Fläche des Dreieckimpulses]] | [[File:P_ID498__Sig_Z_3_2_a_neu.png|right|frame|Fläche des Dreieckimpulses]] | ||
| − | '''(1)''' | + | '''(1)''' The one-sided duration of the symmetrical triangular pulse is $T = 1/f_0\hspace{0.15 cm}\underline{ = 5 \,{\rm µ s}}$. |
| − | * | + | *The spectral value $X_0 = X_1(f = 0)$ indicates the pulse area of $x_1(t)$ an. |
| − | * | + | *This is equal to ${A} \cdot {T}$. From this follows: |
:$$A = \frac{X_0 }{T} = \frac{ 10^{-5}\rm V/Hz }{5 \cdot 10^{-6}{\rm s}}\hspace{0.15 cm}\underline{= 2\;{\rm V}}.$$ | :$$A = \frac{X_0 }{T} = \frac{ 10^{-5}\rm V/Hz }{5 \cdot 10^{-6}{\rm s}}\hspace{0.15 cm}\underline{= 2\;{\rm V}}.$$ | ||
| − | '''(2)''' | + | '''(2)''' The DC component is given by the Dirac weight at $f = 0$ . One obtains ${B} \hspace{0.15 cm}\underline{= -1 \,\text{V}}$. |
| − | '''(3)''' | + | '''(3)''' The two spectral lines at $\pm f_0$ together give a cosine signal with amplitude ${C} \hspace{0.15 cm}\underline{= 1 \text{V}}$. |
| − | '''(4)''' | + | '''(4)''' The maximum value occurs at time ${t} = 0$ (here the triangular pulse and cosine signal are maximum): |
:$$x_{\text{max}} = A + B + C \hspace{0.15 cm}\underline{= +2 \text{V}}.$$ | :$$x_{\text{max}} = A + B + C \hspace{0.15 cm}\underline{= +2 \text{V}}.$$ | ||
| − | * | + | *The minimum values of ${x(t)}$ result when the triangular pulse has decayed and the cosine function delivers the value $–\hspace{-0.08 cm}1 \,\text{V}$ liefert: |
:$$x_\text{min} = {B} - {C}\hspace{0.15 cm}\underline{ = -2\, \text{V}}.$$ | :$$x_\text{min} = {B} - {C}\hspace{0.15 cm}\underline{ = -2\, \text{V}}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 21:06, 20 January 2021
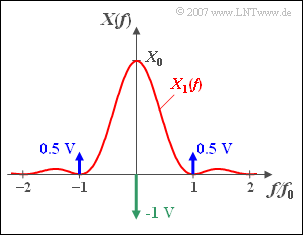
The sketched spectrum ${X(f)}$ of a time signal ${x(t)}$ is composed of
- a continuous component $X_1(f)$,
- plus three dirac-shaped spectral lines.
The continuous component with $f_0 = 200\, \text{kHz}$ and $X_0 = 10^{–5} \text{ V/Hz}$is as follows:
- $$X_1( f ) = X_0 \cdot {\mathop{\rm si}\nolimits} ^2 ( {\pi {f}/{f_0}} ),\quad {\rm where is}\quad {\mathop{\rm si}\nolimits} (x) = {\sin (x)}/{x}.$$
The spectral line at $f = 0$ has the weight $–\hspace{-0.08cm}1\,\text{V}$. In addition, there are two lines at frequencies $\pm f_0$, both with weight $0.5\,\text{V}$.
Hints:
- This exercise belongs to the chapter Fourier Transform and Its Inverse.
- Further information on this topic can be found in the learning video Kontinuierliche und diskrete Spektren.
- It can be assumed as known that a triangular pulse $y(t)$ symmetrical about $t = 0$ with the amplitude ${A}$ and the absolute duration $2T$ $($i.e.: he signal values are unequal to $ 0 $ only between $–T$ and $+T$ ) has the following spectral function:
- $$Y( f ) = A \cdot T \cdot {\rm si}^2 ( \pi f T ).$$
Question
Solution
(1) The one-sided duration of the symmetrical triangular pulse is $T = 1/f_0\hspace{0.15 cm}\underline{ = 5 \,{\rm µ s}}$.
- The spectral value $X_0 = X_1(f = 0)$ indicates the pulse area of $x_1(t)$ an.
- This is equal to ${A} \cdot {T}$. From this follows:
- $$A = \frac{X_0 }{T} = \frac{ 10^{-5}\rm V/Hz }{5 \cdot 10^{-6}{\rm s}}\hspace{0.15 cm}\underline{= 2\;{\rm V}}.$$
(2) The DC component is given by the Dirac weight at $f = 0$ . One obtains ${B} \hspace{0.15 cm}\underline{= -1 \,\text{V}}$.
(3) The two spectral lines at $\pm f_0$ together give a cosine signal with amplitude ${C} \hspace{0.15 cm}\underline{= 1 \text{V}}$.
(4) The maximum value occurs at time ${t} = 0$ (here the triangular pulse and cosine signal are maximum):
- $$x_{\text{max}} = A + B + C \hspace{0.15 cm}\underline{= +2 \text{V}}.$$
- The minimum values of ${x(t)}$ result when the triangular pulse has decayed and the cosine function delivers the value $–\hspace{-0.08 cm}1 \,\text{V}$ liefert:
- $$x_\text{min} = {B} - {C}\hspace{0.15 cm}\underline{ = -2\, \text{V}}.$$