Aufgaben:Exercise 3.4Z: Trapezoid, Rectangle and Triangle

• Return to book

Trapezimpuls und dessen Grenzfälle „Rechteck” und „Dreieck”

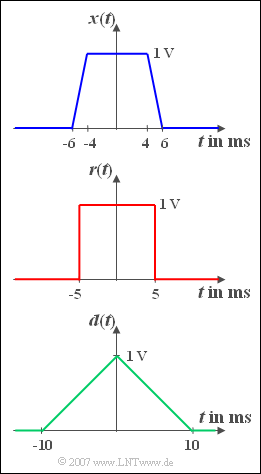
Three different pulse shapes are considered. The pulse  ${x(t)}$  is trapezoidal. For  $| t | < t_1 = 4 \,\text{ms}$ the time course is constant equal to  ${A} = 1\, \text{V}$. Afterwards,  ${x(t)}$  drops linearly to the value zero until the time  $t_2 = 6\, \text{ms}$ . With the two derived system quantities, namely

• the  equivalent bandwidth 

$$\Delta t = t_1 + t_2$$

• and the so-called roll-off factor (in the time domain)

$$r_t = \frac{t_2 - t_1 }{t_2 + t_1 }$$

is the spectral function of the trapezoidal pulse:

$$X( f ) = A \cdot \Delta t \cdot {\mathop{\rm si}\nolimits}( {{\rm \pi} \cdot \Delta t \cdot f} ) \cdot \hspace{0.1cm}{\mathop{\rm si}\nolimits}( {{\rm \pi}\cdot \Delta t \cdot r_t \cdot f} ).$$

Furthermore, the rectangular momentum  ${r(t)}$  and the triangular momentum  ${d(t)}$  are also shown in the graph, both of which can be interpreted as limiting cases of the trapezoidal momentum  ${x(t)}$ .

Hints:

• This exercise belongs to the chapter  Fourier Transform Laws.

• You can check your results using the two interactive applets   Impulses and Spectra  sowie  Frequenzgang und Impulsantwort .

Questions

1

What is the equivalent impulse duration and the rolloff factor of  ${x(t)}$?

$\Delta t \ = \ $  $\text{ms}$

$r_t\hspace{0.3cm} = \ $

2

Which statements are true regarding the spectral function  ${X(f)}$ ?

	The spectral value at frequency  $f = 0$  is equal to  $20 \,\text{mV/Hz}$.
	For the phase function the values  $0$  or  $\pi$  $(180^{\circ})$  are possible.
	${X(f)}$  only has zeros at all multiples of  $100 \,\text{Hz}$  auf.

3

Which statements are true regarding the spectral function  ${R(f)}$  ?

	The spectral value at frequency  $f = 0$  is equal to  ${X(f = 0)}$.
	The values $0$ or  $\pi$  $(180^{\circ})$  are possible for the phase function.
	${R(f)}$  only has zeros at all multiples of   $100 \,\text{Hz}$ auf..

4

Welche Aussagen sind hinsichtlich der Spektralfunktion  ${D(f)}$  zutreffend?

	The spectral value at frequency  $f = 0$  is equal to  ${X(f = 0)}$.
	The values $0$ or  $\pi$  $(180^{\circ})$  are possible for the phase function.
	${D(f)}$  only has zeros at all multiples of   $100 \,\text{Hz}$ auf.

Solution

Solution

(1)  The equivalent pulse duration is  $\Delta t = t_1 + t_2 \;\underline{= 10 \,\text{ms}}$  and the rolloff factor  $r_t = 2/10 \;\underline{= 0.2}$.

(2)  Proposed solutions 2 and 3 are correct:

• The spectral value at  $f = 0$  is  $A \cdot \Delta t = 10 \,\text{mV/Hz}$.
• Since  ${X(f)}$  is real and can assume both positive and negative values, only the two phase values  $0$  und  $\pi$  are possible.
• Zeros exist due to the first si-function at all multiples of  $1/\Delta t = 100\, \text{Hz}$.
• The second si function leads to zero crossings at intervals of  $1/(r_t \cdot \Delta t) = 500 \,\text{Hz}$. These coincide exactly with the zeros of the first si-function.

(3)  All proposed solutions are correct:

• With the equivalent pulse duration  $\Delta t = 10 \,\text{ms}$  and the rolloff factor  $r_t = 0$  one obtains:   $R( f ) = A \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ( {{\rm{\pi }} \cdot \Delta t \cdot f} ).$
• It follows that  $R( f = 0) = A \cdot \Delta t = X( f = 0).$

(4)  Proposed solutions 2 and 3 are correct:

• For the triangular pulse, the rolloff factor is  $r_t = 1$.
• The equivalent pulse duration is  $\Delta t = 10 \,\text{ms}$. It follows that   $D( f ) = A \cdot \Delta t \cdot {\mathop{\rm si}\nolimits} ^2 ( {{\rm{\pi }} \cdot \Delta t \cdot f} )$  and  $D( f = 0) = A \cdot \Delta t = X( f = 0)$.
• Since  ${D(f)}$  cannot become negative, the phase  $[{\rm arc} \; {D(f)}]$  is always zero. The phase value  $\pi$  $(180°)$  is therefore not possible with the triangular form.