Difference between revisions of "Applets:Period Duration of Periodic Signals"
| Line 1: | Line 1: | ||
| − | {{ | + | {{LntAppletLinkEnDe|signalPeriod_en|signalPeriod}} |
| − | |||
| Line 16: | Line 15: | ||
==Theoretical background== | ==Theoretical background== | ||
<br> | <br> | ||
| − | A | + | A periodic signal $x(t)$ is present exactly when it is not constant and if for all arbitrary values of $t$ and all integer values of $i$ with an appropriate $T_{0}$ applies: |
:$$x(t+i\cdot T_{0}) = x(t).$$ | :$$x(t+i\cdot T_{0}) = x(t).$$ | ||
*$T_0$ is called the '''period duration''' and $f_0 = 1/T_0$ the '''basic frequency'''. | *$T_0$ is called the '''period duration''' and $f_0 = 1/T_0$ the '''basic frequency'''. | ||
| Line 160: | Line 159: | ||
==Once again: Open Applet in new Tab== | ==Once again: Open Applet in new Tab== | ||
| − | {{ | + | {{LntAppletLinkEnDe|signalPeriod_en|signalPeriod}} |
| − | |||
<br><br> | <br><br> | ||
Revision as of 14:21, 29 March 2021
Open Applet in new Tab Deutsche Version Öffnen
Contents
Applet Descripition
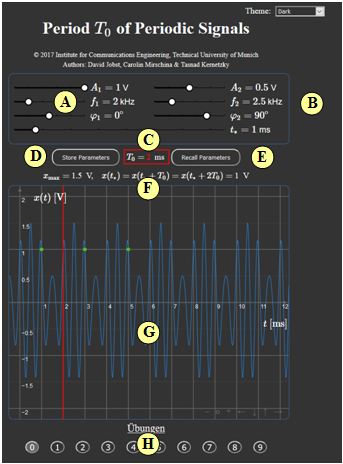
This applet draws the course and calculates the period duration $T_0$ of the periodic function
- $$x(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)+A_2\cdot \cos\left(2\pi f_2\cdot t- \varphi_2\right).$$
Please note:
- The phases $\varphi_i$ must be entered here in radians. Conversion from the input value:
- $$\varphi_i \text{[in radians]} =\varphi_i \text{[in degrees]}/360 \cdot 2\pi.$$
- The maximum value $x_{\rm max}$ and a signal value $x(t_*)$ at a given time $t_*$ are also output.
Theoretical background
A periodic signal $x(t)$ is present exactly when it is not constant and if for all arbitrary values of $t$ and all integer values of $i$ with an appropriate $T_{0}$ applies:
- $$x(t+i\cdot T_{0}) = x(t).$$
- $T_0$ is called the period duration and $f_0 = 1/T_0$ the basic frequency.
- For a harmonic oscillation $x_1(t) = A_1\cdot \cos\left(2\pi f_1\cdot t- \varphi_1\right)$ applies $f_0 = f_1$ and $T_0 = 1/f_1$, independent of the phase $\varphi_1$ and the amplitude $A_1 \ne 0$.
$\text{Calculation Rule: }$ If the periodic signal $x(t)$ consists of two parts $x_1(t)$ and $x_2(t)$ like in this applet, then applies for the basic frequency and the period duration with $A_1 \ne 0$, $f_1 \ne 0$, $A_2 \ne 0$, $f_2 \ne 0$:
- $$f_0 = {\rm gcd}(f_1, \ f_2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}T_0 = 1/f_0.$$
Here $\rm gcd$ denotes the greatest common divisor.
$\text{Examples:}$ In the following $f_0'$, $f_1'$ and $f_2'$ denote signal frequencies normalized to $1\ \rm kHz$:
(a) $f_1' = 1.0$, $f_2' = 3.0$ ⇒ $f_0' = {\rm gcd}(1.0, \ 3.0) = 1.0$ ⇒ $T_0 = 1.0\ \rm ms$;
(b) $f_1' = 1.0$, $f_2' = 3.5$ ⇒ $f_0' = {\rm gcd}(1.0, \ 3.5)= 0.5$ ⇒ $T_0 = 2.0\ \rm ms$;
(c) $f_1' = 1.0$, $f_2' = 2.5$ ⇒ $f_0' = {\rm gcd}(1.0, \ 2.5) = 0.5$ ⇒ $T_0 = 2.0\ \rm ms$;
(d) $f_1' = 0.9$, $f_2' = 2.5$ ⇒ $f_0' = {\rm gcd}(0.9, \ 2.5) = 0.1$ ⇒ $T_0 = 10.0 \ \rm ms$;
(e) $f_2' = \sqrt{2} \cdot f_1' $ ⇒ $f_0' = {\rm gcd}(f_1', \ f_2') \to 0$ ⇒ $T_0 \to \infty$ ⇒ the signal $x(t)$ is not periodic.
$\text{Note:}$ The period duration could also be determined as least common multiple $\rm (lcm)$ according to $T_0 = {\rm lcm}(T_1, \ T_2)$:
- (c) $T_1 = 1.0\ \rm ms$, $T_2 = 0.4\ \rm kHz$ ⇒ $T_0 = {\rm lcm}(1.0, \ 0.4) \ \rm ms = 2.0\ \rm ms$
With all other parameter values, however, there would be numerical problems, for example
- (a) $T_1 = 1.0\ \rm ms$ and $T_2 = 0.333\text{...} \ \rm ms$ have no "least common multiple" due to the limited representation of real numbers.
Exercises
- First select the number (1, 2, ... ) of the exercise. The number 0 corresponds to a "Reset": Same setting as at the program start.
- An exercise description is displayed. Parameter values are adjusted. Solution after pressing "Show solution".
- $A_1'$ and $A_2'$ denote the signal amplitudes normalized to $1\ \rm V$. $f_0'$, $f_1'$ and $f_2'$ are the frequencies normalized to $1\ \rm kHz$.
(1) Consider $A_1' = 1.0, \ A_2' = 0.5, \ f_1' = 2.0, \ f_2' = 2.5, \ \varphi_1 = 0^\circ \ \varphi_2 = 90^\circ$. How large is the period $T_0$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The period is $T_0 = 2.0 \ \rm ms$ due to $\rm{gcd}(2.0, 2.5) = 0.5$.
(2) Vary $\varphi_1$ and $\varphi_2$ in the whole possible range $\pm 180^\circ$. How does this affect the period $T_0$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The period $T_0 = 2.0 \ \rm ms$ remains the same for all $\varphi_1$ and $\varphi_2$.
(3) Select the default setting ⇒ "Recall Parameters". Vary $A_1'$ in the entire possible range $0 \le A_1' \le 1$.
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The period $T_0 = 2.0 \ \rm ms$ remains the same with the exception of $A_1' =0$. In the latter case: $T_0 = 0.4 \ \rm ms$.
(4) Choose the default setting ⇒ "Recall Parameters" and vary $f_2'$. Does this affect $T_0$? Which value is the result for $f_2' = 0.2$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The period jumps back and forth. For $f_2' = 0.2$ the result is $T_0 = 5.0 \ \rm ms$ because of $\ \rm{gcd} (2.0,0.2)=0.2$.
(5) Consider $A_1' = 1.0, \ A_2' = 0.5, \ f_1' = 0.2, \ f_2' = 2.5, \ \varphi_1 = 0^\circ \ \varphi_2 = 90^\circ$. How large is the period $T_0$? Save this setting with "Store Parameters".
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The period is $T_0 = 10.0 \ \rm ms$ due to $\rm{gcd}(0.2, 2.5) = 0.1$.
(6) Select the last setting ⇒ "Recall Parameters" and change $f_2' = 0.6$. Save this setting with "Store Parameters".
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The period is $T_0 = 5.0 \ \rm ms$ due to $\rm{gcd}(0.2,0.6) = 0.2$.
(7) How large is the maximum signal value $x_{\rm max}$ with the same settings?`
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$ $x_{\rm max} =x(t_* + i \cdot T_0) = 1.38 \ {\rm V} < A_1 + A_2$ with $t_* = 0.3 \ \rm ms$ and $T_0 = 5.0 \ \rm ms$.
(8) What changes with $\varphi_2 = 0^\circ$ ⇒ Sum of two cosine waves?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$ $t_* = 0$, $T_0 = 5.0 \ \rm ms$ ⇒ $x_{\rm max} =x(t_* + i \cdot T_0) = 1.5 \ {\rm V}=A_1 + A_2$.
(9) Now consider $\varphi_1 = \varphi_2 = 90^\circ$ ⇒ Sum of two sine waves?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}$The maximum signal value is now $x_{\rm{max}} = 1.07 \ \rm V < A_1 + A_2$. This value results from $T_0 = 5.0 \ \rm ms$ and $t_* = 0.6 \ \rm ms$ or $t_* = 1.9 \ \rm ms$.
Applet Manual
(A) Parameter input for harmonic oscillation 1
(B) Parameter input for harmonic oscillation 2 and time $t_*$.
(C) Numerical output of the main result $T_0$; graphical illustration by red line
(D) Save parameter sets
(E) Retrieve parameter sets
(F) Output of $x_{\rm max}$ and the signal values $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$
(G) Graphic field for displaying the signals
The signal values $x(t_*) = x(t_* + T_0)= x(t_* + 2T_0)$ are marked by green dots
At the bottom of the graphic field you will find the following buttons:
(1) Zoom funktions: „$+$” (Zoom In), „$-$” (Zoom Out), $\rm o$ (Reset)
(2) Move with "←" (Section to the left, ordinate to the right), „$\uparrow$” „$\downarrow$”, „$\rightarrow$”
(H) Task selection according to the task number
In all applets top right: Changeable graphical interface design ⇒ Theme:
- Dark: black background (recommended by the authors).
- Bright: white background (recommended for beamers and printouts)
- Deuteranopia: for users with pronounced green–visual impairment
- Protanopia: for users with pronounced red–visual impairment
About the Authors
This interactive calculation tool was designed and implemented at the Institute for Communications Engineering at the Technical University of Munich.
- The first German version was created in 2004 by Ji Li as part of her diploma thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).
- In 2017 the program was redesigned by David Jobst (Bachelor thesis LB, Supervisor: Tasnád Kernetzky ) via „HTML5”.
- The English version was done in 2020 by Carolin Mirschina. Translation with www.DeepL.com/Translator (free version).