Difference between revisions of "Aufgaben:Exercise 5.3Z: Zero-Padding"
| Line 3: | Line 3: | ||
}} | }} | ||
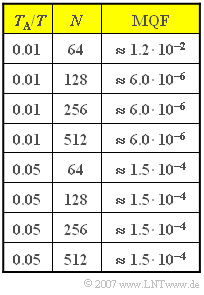
| − | [[File:P_ID1146__Sig_Z_5_3_neu.png|right|frame|$\rm MQF$– | + | [[File:P_ID1146__Sig_Z_5_3_neu.png|right|frame|$\rm MQF$– values as a fuction of $T_{\rm A} /T$ and $N$]] |
We consider the DFT of a rectangular pulse $x(t)$ of height $A =1$ and duration $T$. Thus the spectral function $X(f)$ a $\sin(f)/f$–shaped course. | We consider the DFT of a rectangular pulse $x(t)$ of height $A =1$ and duration $T$. Thus the spectral function $X(f)$ a $\sin(f)/f$–shaped course. | ||
| Line 78: | Line 78: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Proposed solutions 1 and 3</u> are correct: |
| − | * | + | *Already with $N = 128$ , $T_{\rm P} = 1.28 \cdot T$, i.e. larger than the width of the rectangle. |
| − | * | + | *Thus the termination error plays no role at all here. |
| − | * | + | *The $\rm MQF$ value is determined solely by the aliasing error. |
| − | * | + | *The numerical values clearly confirm that $\rm MQF$ is (almost) independent of $N$ ist. |
| − | '''(2)''' | + | '''(2)''' From $T_{\rm A}/T = 0.01$ follows $f_{\rm P} \cdot T = 100$. |
| − | * | + | *The supporting values of $X(f)$ thus lie in the range $–50 ≤ f \cdot T < +50$. |
| − | * | + | *For the distance between two samples in the frequency range, $f_{\rm A} = f_{\rm P}/N$ applies. This gives the following results: |
:*$N = 128$: $f_{\rm A} \cdot T \; \underline{\approx 0.780}$, | :*$N = 128$: $f_{\rm A} \cdot T \; \underline{\approx 0.780}$, | ||
:*$N = 512$: $f_{\rm A} \cdot T \; \underline{\approx 0.195}$. | :*$N = 512$: $f_{\rm A} \cdot T \; \underline{\approx 0.195}$. | ||
| Line 94: | Line 94: | ||
| − | '''(3)''' | + | '''(3)''' The <u>first statement</u> is correct: |
| − | * | + | *For $N = 128$ , the product is $\text{MQF} \cdot f_{\rm A} \approx 4.7 \cdot 10^{-6}/T$. For $N = 512$ , the product is smaller by a factor of about $4$ . |
| − | * | + | *This means that „zero padding” does not achieve greater DFT accuracy, but a finer „resolution” of the frequency range. |
| − | * | + | *The product $\text{MQF} \cdot f_{\rm A}$ takes this fact into account; it should always be as small as possible. |
| − | '''(4)''' | + | '''(4)''' <u>Proposed solutions 1 and 4</u> are correct: |
| − | * | + | *Because of $T_{\rm A} \cdot f_{\rm A} \cdot N = 1$ , a constant $N$ always results in a smaller $f_{\rm A}$ value when $T_{\rm A}$ is increased. |
| − | * | + | *From the table on the information page, one can see that the mean square error $\rm (MQF)$ is significantly increased $($by a factor of about $400)$ . |
| − | * | + | *The effect is due to the aliasing error, since the transition from $T_{\rm A}/T = 0.01$ auf $T_{\rm A}/T = 0.05$ reduces the frequency period by a factor of $5$ . |
| − | * | + | *The termination error, on the other hand, continues to play no role with the square pulse as long as $T_{\rm P} = N \cdot T_{\rm A}$ is greater than the pulse duration $T$. |
| − | '''(5)''' <u> | + | '''(5)''' <u>All statements are true</u>: |
| − | * | + | *With the parameter values $N = 64$ and $T_{\rm A}/T = 0.01$ , an extremely large termination error occurs. |
| − | * | + | *All time coefficients are $1$, so the DFT incorrectly interprets a DC signal instead of the square wave function. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 15:59, 22 March 2021
We consider the DFT of a rectangular pulse $x(t)$ of height $A =1$ and duration $T$. Thus the spectral function $X(f)$ a $\sin(f)/f$–shaped course.
For this special case the influence of the DFT parameter $N$ is to be analysed, whereby the interpolation point distance in the time domain should always be $T_{\rm A} = 0.01T$ bzw. $T_{\rm A} = 0.05T$ .
The resulting values for the mean square error (MSE, here MQF) of the grid values in the frequency domain are given opposite for different values of $N$ :
- $${\rm MQF} = \frac{1}{N}\cdot \sum_{\mu = 0 }^{N-1} \left|X(\mu \cdot f_{\rm A})-\frac{D(\mu)}{f_{\rm A}}\right|^2 \hspace{0.05cm}.$$
Thus, for $T_A/T = 0.01$ , $101$ of the DFT coefficients $d(ν)$ are always different from zero.
- Of these, $99$ have the value $1$ and the two marginal coefficients are each equal to $0.5$.
- If $N$, is increased, the DFT coefficient field is filled with zeros.
- This is then referred to as „zero padding”.
Hints:
- This task belongs to the chapter Possible Errors when Using DFT.
- The theory of this chapter is summarised in the learning video Possible Errors when Using DFT .
Questions
Solution
- Already with $N = 128$ , $T_{\rm P} = 1.28 \cdot T$, i.e. larger than the width of the rectangle.
- Thus the termination error plays no role at all here.
- The $\rm MQF$ value is determined solely by the aliasing error.
- The numerical values clearly confirm that $\rm MQF$ is (almost) independent of $N$ ist.
(2) From $T_{\rm A}/T = 0.01$ follows $f_{\rm P} \cdot T = 100$.
- The supporting values of $X(f)$ thus lie in the range $–50 ≤ f \cdot T < +50$.
- For the distance between two samples in the frequency range, $f_{\rm A} = f_{\rm P}/N$ applies. This gives the following results:
- $N = 128$: $f_{\rm A} \cdot T \; \underline{\approx 0.780}$,
- $N = 512$: $f_{\rm A} \cdot T \; \underline{\approx 0.195}$.
(3) The first statement is correct:
- For $N = 128$ , the product is $\text{MQF} \cdot f_{\rm A} \approx 4.7 \cdot 10^{-6}/T$. For $N = 512$ , the product is smaller by a factor of about $4$ .
- This means that „zero padding” does not achieve greater DFT accuracy, but a finer „resolution” of the frequency range.
- The product $\text{MQF} \cdot f_{\rm A}$ takes this fact into account; it should always be as small as possible.
(4) Proposed solutions 1 and 4 are correct:
- Because of $T_{\rm A} \cdot f_{\rm A} \cdot N = 1$ , a constant $N$ always results in a smaller $f_{\rm A}$ value when $T_{\rm A}$ is increased.
- From the table on the information page, one can see that the mean square error $\rm (MQF)$ is significantly increased $($by a factor of about $400)$ .
- The effect is due to the aliasing error, since the transition from $T_{\rm A}/T = 0.01$ auf $T_{\rm A}/T = 0.05$ reduces the frequency period by a factor of $5$ .
- The termination error, on the other hand, continues to play no role with the square pulse as long as $T_{\rm P} = N \cdot T_{\rm A}$ is greater than the pulse duration $T$.
(5) All statements are true:
- With the parameter values $N = 64$ and $T_{\rm A}/T = 0.01$ , an extremely large termination error occurs.
- All time coefficients are $1$, so the DFT incorrectly interprets a DC signal instead of the square wave function.