Aufgaben:Exercise 3.4Z: Continuous Phase Frequency Shift Keying

• Return to book

Signale zu  $\rm CP– FSK$

Die Grafik zeigt drei FSK–Sendesignale, die sich hinsichtlich des Frequenzhubs  $\Delta f_{\rm A}$  und somit auch durch ihren Modulationsindex

$$h = 2 \cdot \Delta f_{\rm A} \cdot T$$

unterscheiden.

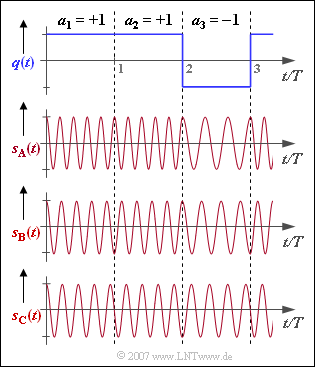
Das digitale Quellensignal  $q(t)$, das den Signalen  $s_{\rm A}(t),  s_{\rm B}(t)$  und  $s_{\rm C}(t)$  zugrundeliegt, ist oben dargestellt. Alle betrachteten Signale sind auf die Amplitude  $1$  und die Zeitdauer  $T$  normiert und basieren auf einem Cosinusträger mit der Frequenz $f_{\rm T}$.

Bei binärer FSK (Binary Frequency Shift Keying) treten nur zwei verschiedene Frequenzen

• $f_{1}$  $($falls  $a_{\nu} = +1)$,
• $f_{2}$  $($falls  $a_{\nu} = -1)$

auf, die jeweils über eine Bitdauer konstant bleiben.

Ist der Modulationsindex kein Vielfaches von  $2$, so ist eine kontinuierliche Phasenanpassung erforderlich, um Phasensprünge zu vermeiden. Man spricht dann von  Continuous Phase Frequency Shift Keying  $(\rm CP– FSK)$.

Ein wichtiger Sonderfall stellt die binäre FSK mit dem Modulationsindex  $h = 0.5$  dar, die auch als  Minimum Shift Keying  $(\rm MSK)$ bezeichnet wird. Diese wird in dieser Aufgabe behandelt.

Hinweise:

• Diese Aufgabe gehört zum Kapitel  Funkschnittstelle.
• Bezug genommen wird insbesondere auf die Seite  Kontinuierliche Phasenanpassung bei FSK.

• Das interaktive Applet  Frequency Shift Keying und Continuous Phase Modulation  verdeutlicht die hier behandelte Thematik.

Fragebogen

1

Welche Aussagen treffen für die FSK und speziell für die MSK zu?

	Die FSK ist im allgemeinen ein nichtlineares Modulationsverfahren.
	Die MSK ist als Offset–QPSK realisierbar und damit linear.
	Es ergibt sich die gleiche Bitfehlerrate wie für die QPSK.
	Eine Bandbegrenzung ist weniger störend als bei QPSK
	Die MSK–Hüllkurve ist auch bei Spektralformumg konstant.

2

Welche Frequenzen  $f_{1}$  $($für Amplitudenkoeffizient  $a_{\nu} = +1)$  und $f_{2}$  $($für  $a_{\nu} = -1)$  beinhaltet das Signal  $s_{\rm A}(t)$?

$f_{1} \cdot T \ = \ $

$f_{2} \cdot T \ = \ $

3

Wie groß sind beim Signal  $s_{\rm A}(t)$  die Trägerfrequenz  $f_{\rm T}$, der Frequenzhub  $\Delta f_{\rm A}$  und der Modulationsindex  $h$?

$f_{\rm T} \cdot T \ = \ $

$\Delta f_{\rm A} \cdot T \ = \ $

$h \ = \ $

4

Wie groß ist der Modulationsindex beim Signal  $s_{\rm B}(t)$?

$h \ = \ $

5

Wie groß ist der Modulationsindex beim Signal  $s_{\rm C}(t)$?

$h \ = \ $

6

Bei welchen Signalen war eine kontinuierliche Phasenanpassung erforderlich?

	$s_{\rm A}(t)$,
	$s_{\rm B}(t)$,
	$s_{\rm C}(t)$.

7

Welche Signale beschreiben  Minimum Shift Keying  (MSK)?

	$s_{\rm A}(t)$,
	$s_{\rm B}(t)$,
	$s_{\rm C}(t)$.

Musterlösung

Solution

(1)  Alle Aussagen mit Ausnahme der dritten treffen zu:

• Die im allgemeinen nichtlineare FSK kann nur kohärent demoduliert werden, während bei MSK auch ein nichtkohärentes Demodulationsverfahren angewendet werden kann.
• Gegenüber der QPSK mit kohärenter Demodulation muss bei der MSK für die gleiche Bitfehlerrate ein um $3 \ \rm dB$ größeres $E_{\rm B}/N_{0}$ (Energie pro Bit bezogen auf die Rauschleistungsdichte) aufgewendet werden.
• Die erste Nullstelle im Leistungsdichtespektrum tritt zwar bei MSK später auf als bei der QSPK, aber es zeigt sich ein schnellerer asymptotischer Abfall als bei QSPK.
• Die konstante Hüllkurve der MSK führt dazu, dass Nichtlinearitäten in der Übertragungsstrecke keine Rolle spielen. Dies ermöglicht den Einsatz einfacher und kostengünstiger Leistungsverstärker mit geringerem Leistungsverbrauch und damit auch längere Betriebsdauern akkubetriebener Geräte.

(2)  Man erkennt aus der Grafik fünf bzw. drei Schwingungen pro Symboldauer:

$$f_{\rm 1} \cdot T \hspace{0.15cm} \underline {= 5}\hspace{0.05cm},\hspace{0.2cm}f_{\rm 2} \cdot T \hspace{0.15cm} \underline { = 3}\hspace{0.05cm}.$$

(3)  Bei FSK mit rechteckförmiger Impulsform treten nur die zwei Augenblicksfrequenzen $f_{1} = f_{\rm T} + \Delta f_{\rm A}$ und $f_{2} = f_{\rm T} – \Delta f_{\rm A}$ auf.

• Mit dem Ergebnis aus (2) erhält man somit:

$$f_{\rm T} \ = \ \frac{f_{\rm 1}+f_{\rm 2}}{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm T} \cdot T \hspace{0.15cm} \underline {= 4}\hspace{0.05cm},$$

$$\Delta f_{\rm A} \ = \ \frac{f_{\rm 1}-f_{\rm 2}}{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\Delta f_{\rm A} \cdot T \hspace{0.15cm} \underline { = 1}\hspace{0.05cm},$$

$$h \ = \ 2 \cdot \Delta f_{\rm A} \cdot T \hspace{0.15cm} \underline {= 2} \hspace{0.05cm}.$$

(4)  Aus der Grafik erkennt man die Frequenzen $f_{1} \cdot T = 4.5$ und $f_{2} \cdot T = 3.5$.

• Daraus ergibt sich der Frequenzhub $\Delta f_{\rm A} \cdot T = 0.5$ und der Modulationsindex $\underline{h = 1}$.

(5)  Hier treten die beiden (normierten) Frequenzen $f_{1} \cdot T = 4.25$ und $f_{2} \cdot T = 3.75$ auf,

• womit sich der Frequenzhub $\Delta f_{\rm A} \cdot T = 0.25$ und der Modulationsindex $\underline{h = 0.5}$ berechnen lassen.

(6)  Richtig sind die Lösungsvorschläge 2 und 3:

• Lediglich bei $s_{\rm A}(t)$ wurde keine Phasenanpassung vorgenommen.
• Hier sind die Signalverläufe im Bereich des ersten und zweiten Bit ($a_{1} = a_{2} = +1$) jeweils cosinusförmig wie das Trägersignal (bezogen auf die Symbolgrenze).
• Dagegen ist im zweiten Symbol von $s_{\rm B}(t)$ ein minus–cosinusförmiger Verlauf (Anfangsphase $\phi_{0} = π$ entsprechend $180^\circ$) zu erkennen und im zweiten Symbol von $s_{\rm C}(t)$ ein minus–sinusförmiger Verlauf ($\phi_{0} = π /2$ bzw. $90^\circ$).
• Bei $s_{\rm A}(t)$ ist die Anfangsphase stets $0$, bei $s_{\rm B}(t)$ entweder $0$ oder $π$, während beim Signal $s_{\rm C}(t)$ mit Modulationsindex $h = 0.5$ insgesamt vier Anfangsphasen möglich sind: $0^\circ, \ 90^\circ, \ 180^\circ$ und $270^\circ$.

(7)  Richtig ist der letzte Lösungsvorschlag, da für dieses Signal $h = 0.5$ gilt.

• Dies ist der kleinstmögliche Modulationsindex, für den Orthogonalität zwischen $f_{1}$ und $f_{2}$ innerhalb der Symboldauer $T$ besteht.