Difference between revisions of "Aufgaben:Exercise 2.6: Modified MS43 Code"
m (Text replacement - "Category:Aufgaben zu Digitalsignalübertragung" to "Category:Digital Signal Transmission: Exercises") |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Digital_Signal_Transmission/Block_Coding_with_4B3T_Codes |
}} | }} | ||
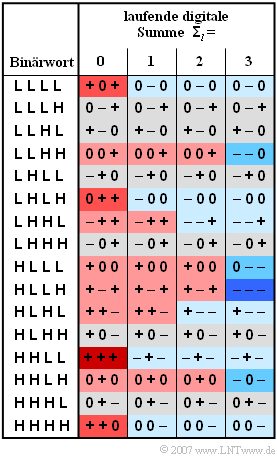
| − | [[File:P_ID1340__Dig_A_2_6.png|right|frame| | + | [[File:P_ID1340__Dig_A_2_6.png|right|frame|Code table of the MMS43 code]] |
| − | + | For ISDN data transmission, the MMS43 code (''Modified Monitored Sum 4B3T'' ) is used in Germany and Belgium on the so-called $\rm {U_{K0}}$ interface, which describes the transmission path between the exchange and home. This is a 4B3T code with four code tables, which are used for coding according to the running digital sum (after $l$ blocks) | |
:$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu$$ | :$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu$$ | ||
| − | + | ${\it \Sigma}_{0} = 0$ is used for initialization. | |
| − | + | The colorings in the table mean: | |
| − | * | + | *If the running digital sum does not change $({\it \Sigma}_{l+1} = {\it \Sigma}_{l})$, a field is grayed out. |
| − | * | + | *An increase $({\it \Sigma}_{l+1} > {\it \Sigma}_{l})$ is highlighted in red, a decrease $({\it \Sigma}_{l+1} < {\it \Sigma}_{l})$ in blue. |
| − | * | + | *The more intense the coloring, the larger the change. |
| Line 18: | Line 18: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Block_Coding_with_4B3T_Codes|Block Coding with 4B3T Codes]]. |
| − | * | + | *The binary symbols are denoted by '''L''' ("Low") and '''H''' ("High") in this learning tutorial. Often you can find the binary symbols '''L''' and '''0''' (instead of '''H''') in the literature. Sometimes, however, '''L''' corresponds to our '''H''' and '''0''' to '''L'''. |
| − | * | + | *To avoid such confusion and to prevent the "0" from appearing in both alphabets (binary and ternary) - in addition with different meanings - we have used the nomenclature which admittedly takes some getting used to. We are well aware that our nomenclature will also confuse some readers. |
| − | * | + | *You can check the results with the interaction module [[Applets:4B3T-Codes|Principle of 4B3T coding]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Why is a 4B3T code used for ISDN instead of the redundancy-free binary code? |
|type="[]"} | |type="[]"} | ||
| − | - 4B3T | + | - 4B3T is always better than the redundancy-free binary code. |
| − | + | + | + The transmitted signal should be equal signal free because of $H_{\rm K}(f=0) = 0$. |
| − | + | + | + A smaller step rate allows longer cable length. |
| − | { | + | {Code the binary sequence $\rm HHLL\hspace{0.08cm} LHLL\hspace{0.08cm} LHHL\hspace{0.08cm} HLHL$ $($with ${\it \Sigma}_{0} = 0)$ . <br>What is the amplitude coefficient of the third ternary symbol of the fourth block? |
|type="{}"} | |type="{}"} | ||
$a_{12} \ = \ $ { -1.03--0.97 } | $a_{12} \ = \ $ { -1.03--0.97 } | ||
| − | { | + | {Determine the Markov diagram for the transition from ${\it \Sigma}_{l}$ to ${\it \Sigma}_{l+1}$. What are the transition probabilities? |
|type="{}"} | |type="{}"} | ||
$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) \ = \ $ { 0.375 3% } | $ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) \ = \ $ { 0.375 3% } | ||
| Line 48: | Line 48: | ||
$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 2) \ = \ $ { 0 3% } | $ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 2) \ = \ $ { 0 3% } | ||
| − | { | + | {What properties follow from the Markov diagram? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - Equal probabilities: ${\rm Pr}({\it \Sigma}_{l} = 0) = \text{...} = {\rm Pr}(\Sigma_{l} = 3)$. |
| − | + | + | + ${\rm Pr}({\it \Sigma}_{l} = 0) = {\rm Pr}({\it \Sigma}_{l} = 3)$ and ${\rm Pr}({\it \Sigma}_{l} = 1) = {\rm Pr}({\it \Sigma}_{l} = 2)$ are valid. |
| − | + | + | + The extreme values $({\it \Sigma}_{l} = 0$ and ${\it \Sigma}_{l} = 3)$ occur less frequently than the inner values $({\it \Sigma}_{l} = 1$ and ${\it \Sigma}_{l} = 2)$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' <u>Statements 2 and 3</u> are correct: |
| − | * | + | *The first statement, on the other hand, is not true: For example, the AWGN (''Additives Weißes Gaußsches Rauschen'') channel with a 4B3T code results in a much larger error probability due to the ternary decision compared to the redundancy-free binary code. The essential reason for the use of a redundant transmission code is rather that no DC signal component can be transmitted via a "telephone channel". |
| − | * | + | *The $25 \%$ smaller step rate $(1/T)$ of the 4B3T code compared to the redundancy-free binary code also accommodates the transmission characteristics of symmetrical copper lines (strong increase in attenuation with frequency). For a given line attenuation, a greater length can be bridged with the 4B3T code than with a redundancy-free binary signal. |
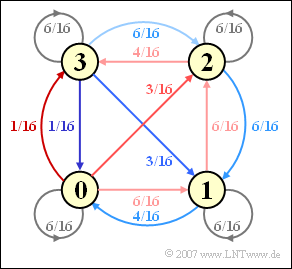
| − | [[File:P_ID1341__Dig_A_2_6c.png|right|frame| | + | [[File:P_ID1341__Dig_A_2_6c.png|right|frame|Markov diagram for the MMS43 code]] |
| − | '''(2)''' | + | '''(2)''' The 4B3T coding results with the initial value ${\it\Sigma}_{0} = 0$: |
*'''HHLL''' ⇒ $+ + + \hspace{0.2cm}({\it\Sigma}_{1} = 3)$, | *'''HHLL''' ⇒ $+ + + \hspace{0.2cm}({\it\Sigma}_{1} = 3)$, | ||
| Line 71: | Line 71: | ||
*'''HLHL''' ⇒ $+ – – \hspace{0.2cm}({\it\Sigma}_{4} = 1)$. | *'''HLHL''' ⇒ $+ – – \hspace{0.2cm}({\it\Sigma}_{4} = 1)$. | ||
| − | + | Thus, the amplitude coefficient we are looking for is $a_{12} \ \underline{= -\hspace{-0.05cm}1}$. | |
| − | '''(3)''' | + | '''(3)''' From the coloring of the code table, the Markov diagram can be obtained. From it, one can read the transition probabilities we are looking for: |
:$$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 6/16 \ \underline{= 0.375},$$ | :$$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 6/16 \ \underline{= 0.375},$$ | ||
| Line 81: | Line 81: | ||
| − | '''(4)''' | + | '''(4)''' <u>Statements 2 and 3</u> are correct: |
| − | * | + | *Statement 1 is false, recognizable by the asymmetries in the Markov diagram. |
| − | * | + | *On the other hand, there are symmetries with respect to the states "$0$" and "$3$" as well as between "$1$" and "$2$". |
| − | *In | + | *In the following calculation, instead of $ {\rm Pr}({\it \Sigma}_{l} = 0$ we write $ {\rm Pr}(0)$ in a simplified way. |
| − | * | + | *Taking advantage of the property ${\Pr}(3) = {\Pr}(0)$ and ${\Pr}(2) = {\Pr}(1)$, we obtain from the Markov diagram: |
:$${\rm Pr}(0)= {6}/{16} \cdot {\rm Pr}(0) +{4}/{16} \cdot {\rm Pr}(1)+ {1}/{16} \cdot {\rm Pr}(3)\hspace{0.15cm} \Rightarrow \hspace{0.15cm}{9}/{16} \cdot {\rm Pr}(0)= {4}/{16} \cdot {\rm Pr}(1)$$ | :$${\rm Pr}(0)= {6}/{16} \cdot {\rm Pr}(0) +{4}/{16} \cdot {\rm Pr}(1)+ {1}/{16} \cdot {\rm Pr}(3)\hspace{0.15cm} \Rightarrow \hspace{0.15cm}{9}/{16} \cdot {\rm Pr}(0)= {4}/{16} \cdot {\rm Pr}(1)$$ | ||
| − | + | From the further condition ${\Pr}(0) + {\Pr}(1) = 1/2$ it follows further: | |
:$${\rm Pr}(0)= {\rm Pr}(3)= {9}/{26}\hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(1)= {\rm Pr}(2)= {4}/{26}\hspace{0.05cm}.$$ | :$${\rm Pr}(0)= {\rm Pr}(3)= {9}/{26}\hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(1)= {\rm Pr}(2)= {4}/{26}\hspace{0.05cm}.$$ | ||
| − | + | This calculation is based on the "sum of incoming arrows in state $0$". | |
| − | + | One could also give equations for the other three states, but they all give the same result: | |
:$${\rm Pr}(1) = \ {6}/{16} \cdot {\rm Pr}(0) + {6}/{16} \cdot {\rm Pr}(1)+ {6}/{16} \cdot {\rm Pr}(2)+{3}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$ | :$${\rm Pr}(1) = \ {6}/{16} \cdot {\rm Pr}(0) + {6}/{16} \cdot {\rm Pr}(1)+ {6}/{16} \cdot {\rm Pr}(2)+{3}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$ | ||
:$$ {\rm Pr}(2) = \ {3}/{16} \cdot {\rm Pr}(0) +{6}/{16} \cdot {\rm Pr}(1)+{6}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$ | :$$ {\rm Pr}(2) = \ {3}/{16} \cdot {\rm Pr}(0) +{6}/{16} \cdot {\rm Pr}(1)+{6}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$ | ||
Revision as of 14:22, 20 April 2022
For ISDN data transmission, the MMS43 code (Modified Monitored Sum 4B3T ) is used in Germany and Belgium on the so-called $\rm {U_{K0}}$ interface, which describes the transmission path between the exchange and home. This is a 4B3T code with four code tables, which are used for coding according to the running digital sum (after $l$ blocks)
- $${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu$$
${\it \Sigma}_{0} = 0$ is used for initialization.
The colorings in the table mean:
- If the running digital sum does not change $({\it \Sigma}_{l+1} = {\it \Sigma}_{l})$, a field is grayed out.
- An increase $({\it \Sigma}_{l+1} > {\it \Sigma}_{l})$ is highlighted in red, a decrease $({\it \Sigma}_{l+1} < {\it \Sigma}_{l})$ in blue.
- The more intense the coloring, the larger the change.
Notes:
- The exercise belongs to the chapter Block Coding with 4B3T Codes.
- The binary symbols are denoted by L ("Low") and H ("High") in this learning tutorial. Often you can find the binary symbols L and 0 (instead of H) in the literature. Sometimes, however, L corresponds to our H and 0 to L.
- To avoid such confusion and to prevent the "0" from appearing in both alphabets (binary and ternary) - in addition with different meanings - we have used the nomenclature which admittedly takes some getting used to. We are well aware that our nomenclature will also confuse some readers.
- You can check the results with the interaction module Principle of 4B3T coding.
Questions
Solution
- The first statement, on the other hand, is not true: For example, the AWGN (Additives Weißes Gaußsches Rauschen) channel with a 4B3T code results in a much larger error probability due to the ternary decision compared to the redundancy-free binary code. The essential reason for the use of a redundant transmission code is rather that no DC signal component can be transmitted via a "telephone channel".
- The $25 \%$ smaller step rate $(1/T)$ of the 4B3T code compared to the redundancy-free binary code also accommodates the transmission characteristics of symmetrical copper lines (strong increase in attenuation with frequency). For a given line attenuation, a greater length can be bridged with the 4B3T code than with a redundancy-free binary signal.
(2) The 4B3T coding results with the initial value ${\it\Sigma}_{0} = 0$:
- HHLL ⇒ $+ + + \hspace{0.2cm}({\it\Sigma}_{1} = 3)$,
- LHLL ⇒ $– + 0 \hspace{0.2cm}({\it\Sigma}_{2} = 3)$,
- LHHL ⇒ $– – + \hspace{0.2cm}({\it\Sigma}_{3} = 2)$,
- HLHL ⇒ $+ – – \hspace{0.2cm}({\it\Sigma}_{4} = 1)$.
Thus, the amplitude coefficient we are looking for is $a_{12} \ \underline{= -\hspace{-0.05cm}1}$.
(3) From the coloring of the code table, the Markov diagram can be obtained. From it, one can read the transition probabilities we are looking for:
- $$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 6/16 \ \underline{= 0.375},$$
- $$ {\rm Pr}({\it \Sigma}_{l+1} = 2\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 0)= 3/16 \ \underline{= 0.1875},$$
- $$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 2) \ \underline{= 0}.$$
(4) Statements 2 and 3 are correct:
- Statement 1 is false, recognizable by the asymmetries in the Markov diagram.
- On the other hand, there are symmetries with respect to the states "$0$" and "$3$" as well as between "$1$" and "$2$".
- In the following calculation, instead of $ {\rm Pr}({\it \Sigma}_{l} = 0$ we write $ {\rm Pr}(0)$ in a simplified way.
- Taking advantage of the property ${\Pr}(3) = {\Pr}(0)$ and ${\Pr}(2) = {\Pr}(1)$, we obtain from the Markov diagram:
- $${\rm Pr}(0)= {6}/{16} \cdot {\rm Pr}(0) +{4}/{16} \cdot {\rm Pr}(1)+ {1}/{16} \cdot {\rm Pr}(3)\hspace{0.15cm} \Rightarrow \hspace{0.15cm}{9}/{16} \cdot {\rm Pr}(0)= {4}/{16} \cdot {\rm Pr}(1)$$
From the further condition ${\Pr}(0) + {\Pr}(1) = 1/2$ it follows further:
- $${\rm Pr}(0)= {\rm Pr}(3)= {9}/{26}\hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(1)= {\rm Pr}(2)= {4}/{26}\hspace{0.05cm}.$$
This calculation is based on the "sum of incoming arrows in state $0$".
One could also give equations for the other three states, but they all give the same result:
- $${\rm Pr}(1) = \ {6}/{16} \cdot {\rm Pr}(0) + {6}/{16} \cdot {\rm Pr}(1)+ {6}/{16} \cdot {\rm Pr}(2)+{3}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$
- $$ {\rm Pr}(2) = \ {3}/{16} \cdot {\rm Pr}(0) +{6}/{16} \cdot {\rm Pr}(1)+{6}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$
- $${\rm Pr}(3) = \ {1}/{16} \cdot {\rm Pr}(0) + {4}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm}.$$