Aufgaben:Exercise 1.2: Entropy of Ternary Sources

• Return to book

Probabilities of two ternary sources

The entropy of a discrete-value memoryless message source with  $M$  possible symbols is:

$$H = \sum_{\mu = 1}^M p_{\mu} \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p_\mu}\hspace{0.05cm},\hspace{0.3cm} {\rm pseudo unit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$

Here, the  $p_\mu$  denote the occurrence probabilities of the individual symbols or events.  n the present example, the events are denoted by  $\rm R$(ed),  $\rm G$(reen)  and  $\rm S$(chwarz)  with Schwarz being the German word for black.

• For a binary source with the occurrence probabilities  $p$  and  $1-p$  this can be written:

$$H = H_{\rm bin}(p) = p \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{p}+ (1-p) \cdot {\rm log}_2\hspace{0.1cm}\frac{1}{1-p}\hspace{0.05cm},\hspace{0.3cm} {\rm pseudo unit\hspace{-0.15cm}: \hspace{0.15cm}bit}\hspace{0.05cm}.$$

• The entropy of a multilevel source can often be expressed with this  „binary entropy function”  $H_{\rm bin}(p)$ .

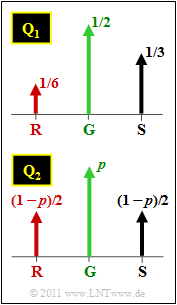
In this task, two ternary sources with the symbol probabilities according to the above graph are considered:

• source  $\rm Q_1$ with  $p_{\rm G }= 1/2$,  $p_{\rm S }= 1/3$  and  $p_{\rm R }= 1/6$,
• source  $\rm Q_2$ with  $p_{\rm G }= p$  and  $p_{\rm S } = p_{\rm R } = (1-p)/2$.

The ternary source  $\rm Q_2$  can also be applied to roulette when a player bets only on the squares  $\rm R$,  $\rm S$chwarz  and $\rm G$reen  (the „zero”).  This type of game is referred to as  $\text{Roulette 1}$  in the question section.

In contrast,  $\text{Roulette 2}$  indicates that the player bets on single numbers  $(0$, ... , $36)$ .

Hint:

• The task belongs to the chapter  Discrete Memoryless Sources.

Questions

1

What is the entropy  $H$  of the source  $\rm \underline{Q_1}$?

$H \ = \ $ $\ \rm bit$

2

Which of the following statements are true if  $\rm R$,  $\rm G$  and  $\rm S$  are represented by the numerical values  $-1$,  $0$  and  $+1$ ?

	The result is a smaller entropy.
	The entropy remains the same.
	The result is a greater entropy.

3

Determine the entropy of the source  $\rm \underline{Q_2}$  using the binary entropy function  $H_{\rm bin}(p)$.  What value results for  $\underline{p = 0.5}$?

$H \ = \ $ $\ \rm bit$

4

For whic  $p$–value der Quelle  $\rm \underline{Q_2}$  does the maximum entropy result:  $H → H_\text{max}$?

$p \ = \ $

5

What is the entropy of the message source  $\text{Roulette 1}$,  i.e. with respect to the events  $\rm R$ed,  $\rm S$chwarz  and  $\rm G$reen  (the „zero”)?

$H \ = \ $ $\ \rm bit$

6

What is the entropy of  $\text{Roulette 2}$ ,  i.e. with regard to the numbers   $0$, ... , $36$?

$H \ = \ $ $\ \rm bit$

Solution

Solution

(1)  Mit den Auftrittswahrscheinlichkeiten  $1/2$,  $1/3$  und  $1/6$  erhält man folgenden Entropiewert:

$$H \hspace{0.1cm} = \hspace{0.1cm} 1/2 \cdot {\rm log}_2\hspace{0.1cm}(2) +1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) +1/6 \cdot {\rm log}_2\hspace{0.1cm}(6) =(1/2 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(2) + (1/3 + 1/6)\cdot {\rm log}_2\hspace{0.1cm}(3) \hspace{0.15cm}\underline {\approx 1.46 \, {\rm bit}} \hspace{0.05cm}.$$

(2)  Richtig ist der Lösungsvorschlag 2:

• Die Entropie hängt nur von den Auftrittswahrscheinlichkeiten ab.
• Es ist dabei egal, welche Zahlenwerte oder physikalische Größen man den einzelnen Symbolen zuordnet.
• Anders ist es bei Mittelwerten oder der AKF–Berechnung.  Werden nur Symbole angegeben, so kann man hierfür keine Momente angeben.
• Außerdem hängen die Mittelwerte, Autokorrelation, usw. davon ab, ob man die Zuordnung bipolar  $(-1, \hspace{0.10cm}0, \hspace{0.05cm}+1)$  oder unipolar  $(0, \hspace{0.05cm}1, \hspace{0.05cm}2)$  vereinbart.

(3)  Die Entropie der Quelle  $\rm Q_2$  lässt sich wie folgt ausdrücken:

$$H \hspace{0.1cm} = \hspace{0.1cm} p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ 2 \cdot \frac{1-p}{2} \cdot {\rm log}_2\hspace{0.1cm}\frac {2}{1-p}= p \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{p}+ (1-p) \cdot {\rm log}_2\hspace{0.1cm}\frac {1}{1-p} + (1-p)\cdot {\rm log}_2\hspace{0.1cm}(2)= H_{\rm bin}(p) + 1-p \hspace{0.05cm}.$$

• Für  $p = 0.5$   ⇒   $H_{\rm bin}(p) = 1$  ergibt sich  $\underline{H = 1.5\hspace{0.05cm}\rm bit}$.

(4)  Die maximale Entropie einer gedächtnislosen Quelle mit dem Symbolumfang $M$ ergibt sich, wenn alle  $M$  Symbole gleichwahrscheinlich sind.

• Für den Sonderfall $M=3$ folgt daraus:

$$p_{\rm R} + p_{\rm G} + p_{\rm S} = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {p = 1/3 \approx 0.333}\hspace{0.05cm}.$$

• Damit erhält man mit dem Ergebnis der Teilaufgabe  (3)  die folgende Entropie:

$$H = H_{\rm bin}(1/3) + 1-1/3 = 1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3/2) + 2/3 $$

$$\Rightarrow \hspace{0.3cm}H = 1/3 \cdot {\rm log}_2\hspace{0.1cm}(3) + 2/3 \cdot {\rm log}_2\hspace{0.1cm}(3) - 2/3 \cdot {\rm log}_2\hspace{0.1cm}(2)+ 2/3 = {\rm log}_2\hspace{0.1cm}(3) = {1.585 \, {\rm bit}} \hspace{0.05cm}.$$

(5)  Das System  $\text{Roulette 1}$  ist informationstheoretisch gleich der Konfiguration  $\rm Q_2$  mit  $p = 1/37$:

$$p_{\rm G} = p = \frac{1}{37}\hspace{0.05cm},\hspace{0.2cm} p_{\rm R} = p_{\rm S} = \frac{1-p}{2} = \frac{18}{37} \hspace{0.05cm}.$$

• Damit erhält man mit dem Ergebnis der Teilaufgabe  (3):

$$H = H_{\rm bin}(1/37) + \frac{36}{37} = \frac{1}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}(37) - \frac{36}{37} \cdot {\rm log}_2\hspace{0.1cm}36 + \frac{36}{37} = {\rm log}_2\hspace{0.1cm}(37) + \frac{36}{37} \cdot ( 1- {\rm log}_2\hspace{0.1cm}(36)) = 5.209 - 4.057 \hspace{0.15cm} \underline { = 1.152 \, {\rm bit}} \hspace{0.05cm}.$$

(6)  Setzt man bei Roulette auf einzelne Zahlen   ⇒   Konfiguration  $\text{Roulette 2}$, so sind alle Zahlen von  $0$  bis  $36$  gleichwahrscheinlich und man erhält:

$$H = {\rm log}_2\hspace{0.1cm}(37) \hspace{0.15cm} \underline { = 5.209 \, {\rm bit}} \hspace{0.05cm}.$$