Difference between revisions of "Theory of Stochastic Signals/Uniformly Distributed Random Variables"
m (Text replacement - "„" to """) |
|||
| Line 1: | Line 1: | ||
{{Header | {{Header | ||
| − | |Untermenü= | + | |Untermenü=Continuous Random Variables |
| − | |Vorherige Seite= | + | |Vorherige Seite=Expected Values and Moments |
| − | |Nächste Seite= | + | |Nächste Seite=Gaussian Distributed Random Variables |
}} | }} | ||
| − | == | + | ==General description and definition== |
<br> | <br> | ||
| − | [[File:P_ID45__Sto_T_3_4_S1_neu100.png |frame| | + | [[File:P_ID45__Sto_T_3_4_S1_neu100.png |frame|PDF and CDF of uniform distribution]] |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ | + | $\text{Definition:}$ A random variable $x$ is said to be '''uniformly distributed''' if it can only take values in the range of $x_{\rm min}$ to $x_{\rm max}$ with equal probability. |
| − | + | The graph shows | |
| − | * | + | *on the left the probability density function $f_{x}(x)$, |
| − | * | + | *right the distribution function $F_{x}(r)$ |
| − | + | of such an equally distributed random variable $x$.}} | |
| − | + | From the graph and the definition, the following properties can be derived: | |
| − | * | + | *The probability density function $\rm (PDF)$ has in the range from $x_{\rm min}$ to $x_{\rm max}$ the constant value $1/(x_{\rm max} - x_{\rm min})$. |
| − | * | + | *On the range limits, only half the value - that is, the average value between the left-hand and right-hand limits - is to be set for $f_{x}(x)$ in each case. |
| − | * | + | *The distribution function $\rm (CDF)$ increases linearly from $x_{\rm min}$ to $x_{\rm max}$ in the range from $0$ to $1$ . |
| − | * | + | *Mean and dispersion have the following values for the uniform distribution: |
:$$m_{\rm 1} = \frac{\it x_ {\rm max} \rm + \it x_{\rm min}}{2},\hspace{0.5cm} | :$$m_{\rm 1} = \frac{\it x_ {\rm max} \rm + \it x_{\rm min}}{2},\hspace{0.5cm} | ||
\sigma = \frac{\it x_{\rm max} - \it x_{\rm min}}{2 \sqrt{3}}.$$ | \sigma = \frac{\it x_{\rm max} - \it x_{\rm min}}{2 \sqrt{3}}.$$ | ||
| − | * | + | *For symmetric PDF ⇒ $x_{\rm min} = -x_{\rm max}$ we obtain as a special case the mean $m_1 = 0$ and the variance $σ^2 = x_{\rm max}^2/3.$ |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{ | + | $\text{Example 1:}$ |
| − | + | The graph shows two signal waveforms with uniform amplitude distribution. | |
| − | [[File:P_ID618__Sto_T_3_4_S2_neu100.png |right|frame| | + | [[File:P_ID618__Sto_T_3_4_S2_neu100.png |right|frame|Examples of uniformly distributed signals]] |
| − | * | + | *On the left, statistical independence of the individual samples is assumed, that is,the random variable $x_ν$ can take all values between $x_{\rm min}$ and $x_{\rm max}$ with equal probability, and independently of the past $(x_{ν-1}, x_{ν-2}, \hspace{0.1cm}\text{...}).$ |
| − | * | + | *For the right signal $y(t)$ this independence of successive signal values is no longer given Rather, this sawtooth signal represents a deterministic signal. |
}} | }} | ||
Revision as of 23:24, 28 December 2021
Contents
General description and definition
$\text{Definition:}$ A random variable $x$ is said to be uniformly distributed if it can only take values in the range of $x_{\rm min}$ to $x_{\rm max}$ with equal probability.
The graph shows
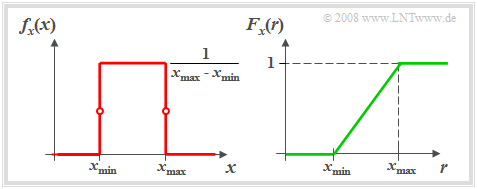
- on the left the probability density function $f_{x}(x)$,
- right the distribution function $F_{x}(r)$
of such an equally distributed random variable $x$.
From the graph and the definition, the following properties can be derived:
- The probability density function $\rm (PDF)$ has in the range from $x_{\rm min}$ to $x_{\rm max}$ the constant value $1/(x_{\rm max} - x_{\rm min})$.
- On the range limits, only half the value - that is, the average value between the left-hand and right-hand limits - is to be set for $f_{x}(x)$ in each case.
- The distribution function $\rm (CDF)$ increases linearly from $x_{\rm min}$ to $x_{\rm max}$ in the range from $0$ to $1$ .
- Mean and dispersion have the following values for the uniform distribution:
- $$m_{\rm 1} = \frac{\it x_ {\rm max} \rm + \it x_{\rm min}}{2},\hspace{0.5cm} \sigma = \frac{\it x_{\rm max} - \it x_{\rm min}}{2 \sqrt{3}}.$$
- For symmetric PDF ⇒ $x_{\rm min} = -x_{\rm max}$ we obtain as a special case the mean $m_1 = 0$ and the variance $σ^2 = x_{\rm max}^2/3.$
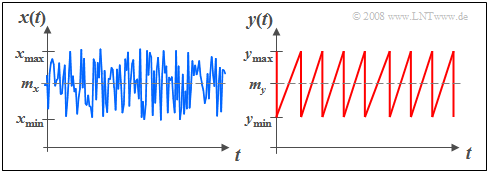
$\text{Example 1:}$ The graph shows two signal waveforms with uniform amplitude distribution.
- On the left, statistical independence of the individual samples is assumed, that is,the random variable $x_ν$ can take all values between $x_{\rm min}$ and $x_{\rm max}$ with equal probability, and independently of the past $(x_{ν-1}, x_{ν-2}, \hspace{0.1cm}\text{...}).$
- For the right signal $y(t)$ this independence of successive signal values is no longer given Rather, this sawtooth signal represents a deterministic signal.
Bedeutung der Gleichverteilung für die Nachrichtentechnik
Die Bedeutung gleichverteilter Zufallsgrößen für die Informations– und Kommunikationstechnik ist darauf zurückzuführen, dass diese WDF–Form aus Sicht der Informationstheorie unter der Nebenbedingung Spitzenwertbegrenzung ein Optimum darstellt:
- Mit keiner anderen Verteilung als der Gleichverteilung erreicht man unter dieser Voraussetzung eine größere differentielle Entropie.
- Mit dieser Thematik beschäftigt sich das Kapitel Differentielle Entropie im Buch "Informationstheorie".
Daneben sind unter Anderem noch folgende Punkte zu nennen:
(1) Die Bedeutung der Gleichverteilung für die Simulation nachrichtentechnischer Systeme ist darauf zurückzuführen, dass man entsprechende "Pseudo–Zufallsgeneratoren" relativ einfach realisieren kann, und dass sich daraus andere Verteilungen wie zum Beispiel die Gaußverteilung und die Exponentialverteilung leicht ableiten lassen.
(2) In der Bildverarbeitung & Bildcodierung wird oft vereinfachend mit der Gleichverteilung anstelle der tatsächlichen, meist sehr viel komplizierteren Verteilung des Originalbildes gerechnet, da der Unterschied des Informationsgehaltes zwischen natürlichem Bild und dem auf der Gleichverteilung basierenden Modell relativ gering ist.
(3) Für die Modellierung übertragungstechnischer Systeme sind gleichverteilte Zufallsgrößen dagegen die Ausnahme. Ein Beispiel für eine tatsächlich (nahezu) gleichverteilte Zufallsgröße ist die Phase bei kreissymmetrischen Störungen, wie sie beispielsweise bei Quadratur–Amplitudenmodulationsverfahren (QAM) auftreten.
Das interaktive Applet WDF, VTF und Momente spezieller Verteilungen berechnet alle Kenngrößen der Gleichverteilung für beliebige Parameter $x_{\rm min}$ und $x_{\rm max}$.
Erzeugung einer Gleichverteilung mit Pseudo–Noise–Generatoren
$\text{Definition}$ Die heute verwendeten Zufallsgeneratoren sind meist pseudozufällig. Das bedeutet,
- dass die erzeugte Folge als das Ergebnis eines festen Algorithmuses eigentlich deterministisch ist,
- für den Anwender jedoch aufgrund der großen Periodenlänge $P$ als stochastisch erscheint.
Mehr hierzu im Kapitel Erzeugung von diskreten Zufallsgrößen.
Für die Systemsimulation haben Pseudo–Noise $\rm (PN)$–Generatoren gegenüber echten Zufallsgeneratoren den entscheidenden Vorteil, dass die erzeugten Zufallsfolgen ohne Speicherung reproduzierbar sind, was
- zum einen den Vergleich verschiedener Systemmodelle ermöglicht, und
- auch die Fehlersuche wesentlich erleichtert.
Ein Zufallsgenerator sollte dabei folgende Kriterien erfüllen:
(1) Die Zufallsgrößen $x_ν$ einer generierten Folge sollten mit sehr guter Näherung gleichverteilt sein. Bei wertdiskreter Darstellung an einem Rechner erfordert dies unter anderem eine hinreichend hohe Bitauflösung, zum Beispiel mit $32$ oder $64$ Bit pro Abtastwert.
(2) Bildet man aus der sequentiellen Zufallsfolge $〈x_ν〉$ jeweils nichtüberlappende Paare von Zufallsgrößen, beispielsweise $(x_ν, x_{ν+1})$, $(x_{ν+2}$, $x_{ν+3})$, ... , so sollten diese Tupel in einer zweidimensionalen Darstellung innerhalb eines Quadrates ebenfalls gleichverteilt sein.
(3) Bildet man aus der sequentiellen Folge $〈x_ν〉$ nicht überlappende $n$–Tupel von Zufallsgrößen ⇒ $(x_ν$, ... , $x_{ν+n–1})$, $(x_{ν+n}$, ... , $x_{ν+2n–1})$ usw., so sollten auch diese innerhalb eines $n$–dimensionalen Würfels möglichst die Gleichverteilung ergeben.
Anmerkung:
- Die erste Forderung bezieht sich ausschließlich auf die Amplitudenverteilung $\rm (WDF)$ und ist im Allgemeinen leichter zu erfüllen.
- Die weiteren Forderungen gewährleisten eine „ausreichende Zufälligkeit” der Folge. Sie betreffen die statistische Unabhängigkeit aufeinander folgender Zufallswerte.
Multiplicative Congruental Generator
$\text{Multiplicative Congruental Generator}$ ist das bekannteste Verfahren zur Erzeugung einer Folge $〈 x_\nu 〉$ mit gleichverteilten Werten $ x_\nu$ zwischen $0$ und $1$. Diese Methode wird hier stichpunktartig angegeben:
(1) Diese Zufallsgeneratoren basieren auf der sukzessiven Manipulation einer Integervariablen $k$. Geschieht die Zahlendarstellung im Rechner mit $L$ Bit, so nimmt diese Variable bei geeigneter Behandlung des Vorzeichenbits alle Werte zwischen $1$ und $2^{L − 1}$ jeweils genau einmal an.
(2) Die hieraus abgeleitete Zufallsgröße $x={k}/{\rm 2^{\it L - \rm 1}}$ ist ebenfalls diskret $($mit Stufenzahl $M = 2^{L– 1})$:
- $$x={k}/{\rm 2^{\it L - \rm 1}} = k\cdot \Delta x \in \{\Delta x, \hspace{0.05cm}2\cdot \Delta x,\hspace{0.05cm}\text{ ...}\hspace{0.05cm} , \hspace{0.05cm}1-\Delta x,\hspace{0.05cm} 1\}.$$
- Ist die Bitanzahl $L$ hinreichend groß, so ist der Abstand $Δx = 1/2^{L– 1}$ zwischen zwei möglichen Werten sehr klein, und man kann $x$ im Rahmen der Simulationsgenauigkeit durchaus als eine wertkontinuierliche Zufallsgröße interpretieren.
(3) Die rekursive Generierungsvorschrift eines solchen Multiplicative Congruential Generators lautet:
- $$k_\nu=(a\cdot k_{\nu-1})\hspace{0.1cm} \rm mod \hspace{0.1cm} \it m.$$
(4) Die statistischen Eigenschaften der Folge hängen entscheidend von den Parametern $a$ und $m$ ab. Der Startwert $k_0$ hat dagegen für die Statistik eine eher untergeordnete Bedeutung.
(5) Die besten Ergebnisse erzielt man mit der Basis $m =2\hspace{0.05cm}^l-1$, wobei $l$ eine beliebige natürliche Zahl angibt. Weit verbreitet ist bei Rechnern mit 32 Bit-Architektur und einem Vorzeichenbit die Basis $m = 2^{31} - 1 = 2\hspace{0.08cm}147\hspace{0.08cm}483\hspace{0.08cm}647$. Ein entsprechender Algorithmus lautet:
- $$k_\nu=(16807\cdot k_{\nu-1})\hspace{0.1cm} \rm mod\hspace{0.1cm}(2^{31}-1).$$
(6) Für einen solchen Generator ist nur der Startwert $k_0 = 0$ nicht erlaubt. Für $k_0 \ne 0$ beträgt die Periodendauer $P = 2^{31} - 2.$
$\text{Beispiel 2:}$ Wir analysieren den oben beschriebenen Multiplicative Congruental Generator genauer:
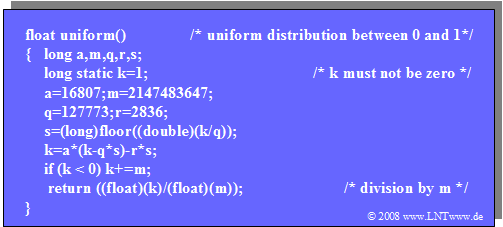
- Den Algorithmus kann man allerdings auf einem 32 Bit–Rechner nicht direkt implementieren, da das Multiplikationsergebnis bis zu 46 Bit benötigt.
- Er kann aber so abgewandelt werden, dass zu keinem Zeitpunkt der Berechnung der 32 Bit–Integerzahlenbereich überschritten wird.
- Das so modifizierte C-Programm $\text{uniform( )}$ ist rechts angegeben.
Aufgaben zum Kapitel
Aufgabe 3.5: Dreieck– und Trapezsignal