Difference between revisions of "Aufgaben:Exercise 2.3: About the LZ78 Compression"
| Line 107: | Line 107: | ||
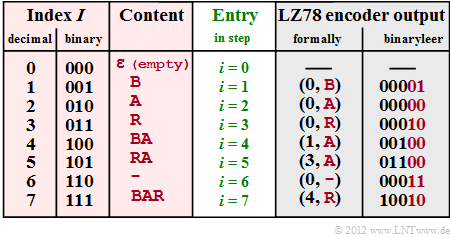
| − | [[File: | + | [[File:EN_Inf_A_2_3f.png|right|frame|LZ78–Codierung von <b>BARBARA–BAR</b>]] |
'''(5)''' Der gesamte Codiervorgang ist in einer Tabelle zusammengefasst. Man erkennt: | '''(5)''' Der gesamte Codiervorgang ist in einer Tabelle zusammengefasst. Man erkennt: | ||
* Zu jedem Zeitpunkt $i$ wird die bearbeitete Zeichenfolge in das Wörterbuch eingetragen. | * Zu jedem Zeitpunkt $i$ wird die bearbeitete Zeichenfolge in das Wörterbuch eingetragen. | ||
Revision as of 14:38, 8 July 2021
In contrast to entropy coding according to Huffman or Shannon, where one must know the source statistics (as precisely as possible), such restrictions do not apply to the compression methods developed by Abraham Lempel and Jacob Ziv . This is called universal source coding.
In this task, we consider the variant first published in 1978 [LZ78]. The string BARBARA–BAR is to be encoded.
- The procedure LZ78 works with a global dictionary, which is initially only filled with an empty character $(\varepsilon)$ under the index $I = 0$ . This distinguishes "LZ78" from its predecessor "LZ77" (with local dictionary) and also from its successor "LZW" (dictionary is prefilled with the possible characters).
- f a character or a word fragment (several characters) of the input string is found in the dictionary, the index $I_0$ of this entry is output together with the next input character $Z$ . In each step $i$ the output is therefore: $(I_0, \ Z)$.
- Afterwards, the new string is entered into the dictionary under the next free index $I_{\rm neu}$ .
- If one considers the dictionary as a field $W\big[\hspace{0.05cm}I\hspace{0.05cm}\big]$ with $I ≥ 0$, where each element contains a string of arbitrary length, then with the character variable $Z$:
- $$W \big[\hspace{0.05cm}I_{\rm neu}\hspace{0.05cm}\big] = W\big[\hspace{0.05cm}I_0\hspace{0.05cm}\big] + Z \hspace{0.05cm}. $$
For clarification, a simple example:
- At a given time, the dictionary is filled up to index $I_{\rm akt }= 20$ .
- Handy is waiting to be encoded. In the dictionary, the Ha is found under index $I = 11$ and the entry Han under index $I = 16$ .
- Thus, the current code output is $(I_0, Z) = (16,$ d$)$ and the following is entered into the dictionary as a new phrase: $W(21) =$ Hand.
- Now the string y is available for coding. If no suitable entry is found, $(0,$ y$)$ is output and a new entry is made in the dictionary: $W(22) = $ $\rm ε$ + y $=$ y .
For subtask (6) you can assume the following:
- The decimal number $I$ (index) is represented in binary by three bits.
- The character $Z ∈ \{$A, B, R, –$ \}$ is binary coded by two bits each.
Hints:
- The task belongs to the chapter Compression According to Lempel, Ziv and Welch.
- In particular, reference is made to the page The Lempel-Ziv Variant LZ78 .
- The original literature [LZ78] on this method is:
Ziv, J.; Lempel, A.: Compression of Individual Sequences via Variable-Rate Coding. In: IEEE Transactions on Information Theory, no. 5, vol. 24, 1978, p. 530–536.
- Exercise 2.3Z and Exercise 2.4 deal with other–Ziv methods in a similar way.
Questions
Musterlösung
- Die Vorbelegung gemäß Aussage 2 gilt dagegen für den LZW–Algorithmus, der 1983 gemeinsam mit Terry Welch veröffentlicht wurde.
(2) $\rm ε$ bezeichnet das leere Zeichen.
- Da $\rm ε$ + B = B ergibt, sind die Aussagen 1 und 2 richtig.
- Aussage 3 trifft wieder nur für die LZW–Komprimierung zu.
(3) Hier treffen beide Aussagen zu.
(4) Richtig sind die Aussagen 2 und 4:
- Im Wörterbuch wird unter dem Index $I = 1$ das Zeichen B gefunden.
- Das nächste Zeichen A der Eingangsfolge wird angehängt: (1, A).
- Die Aussage 3 kann schon deshalb nicht stimmen, da $Z$ nur ein Zeichen sein kann und keine Zeichenfolge.
(5) Der gesamte Codiervorgang ist in einer Tabelle zusammengefasst. Man erkennt:
- Zu jedem Zeitpunkt $i$ wird die bearbeitete Zeichenfolge in das Wörterbuch eingetragen.
- Zum Zeitpunkt $\underline{i=7}$ ist der Codiervorgang abgeschlossen.
(6) Stellt man alle Indizes mit drei Bit dar und die vier Zeichen (Character) mit je zwei Bit, so kommt man zu folgenden Ergebnissen:
- ohne Codierung: $N = 11 \cdot 2 \hspace{0.15cm}\underline {= 22 \, \rm Bit}$,
- mit LZ78–Codierung: $N = 7 \cdot (3+2) \hspace{0.15cm}\underline {= 35 \, \rm Bit}$.
Daran erkennt man:
- Eine jede LZ–Komprimierung macht erst bei einer größeren Datei Sinn, auch dann, wenn man glaubt, dass ein Text wie BARBARA–BAR dem LZ78–Algorithmus entgegenkommt.
- Mit variabler Bitanzahl für den Index entsprechend der Aufgabe 2.4 würde sich für dieses LZ78-Beispiel ergeben:
- $$N = 1 \cdot 3 + 2 \cdot 4 + 4 \cdot 5 = 31 \,{\rm Bit}\hspace{0.05cm}.$$