Difference between revisions of "Aufgaben:Exercise 2.5: Residual Redundancy with LZW Coding"
| Line 4: | Line 4: | ||
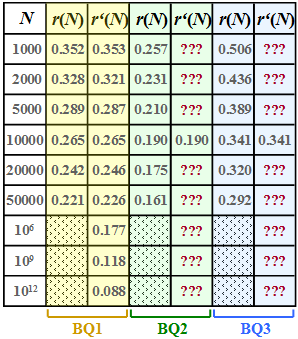
[[File:P_ID2446__Inf_A_2_5_neu.png|right|frame|Residual redundancy $r(N)$ & approximation $r\hspace{0.05cm}'(N)$ of three binary sources]] | [[File:P_ID2446__Inf_A_2_5_neu.png|right|frame|Residual redundancy $r(N)$ & approximation $r\hspace{0.05cm}'(N)$ of three binary sources]] | ||
| − | + | We assume here a binary input sequence of length $N$ and consider three different binary message sources: | |
| − | * $\rm BQ1$: | + | * $\rm BQ1$: Symbol probabilities $p_{\rm A} = 0.89$ and $p_{\rm B} = 0.11$, i.e. different<br> ⇒ entropy $H = 0.5\text{ bit/source symbol}$ ⇒ the source is redundant. |
| − | * $\rm BQ2$: $p_{\rm A} = p_{\rm B} = 0.5$ ( | + | * $\rm BQ2$: $p_{\rm A} = p_{\rm B} = 0.5$ (equally probable)<br> ⇒ entropy $H = 1\text{ bit/source symbol}$ ⇒ the source is redundancy-free. |
| − | * $\rm BQ3$: | + | * $\rm BQ3$: There is no concrete information on the statistics here. <br>In subtask '''(6)''' you are to estimate the entropy $H$ of this source. |
| − | + | For these three sources, the respective <i>residual redundancy</i> $r(N)$ was determined by simulation, which remains in the binary sequence after [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#The_Lempel-Ziv-Welch_algorithm |Lempel–Ziv–Welch–coding]] in der Binärfolge verbleibt. | |
| − | + | The results are shown in the first column of the above table for the sources | |
| − | *$\rm BQ1$ ( | + | *$\rm BQ1$ (yellow background), |
| − | *$\rm BQ2$ ( | + | *$\rm BQ2$ (green background) and |
| − | *$\rm BQ3$ ( | + | *$\rm BQ3$ (blue background) |
| − | + | whereby we have restricted ourselves to sequence lengths $N ≤ 50000$ in the simulation. | |
| − | + | The <i>relative redundancy of the output sequence</i> – simplified called <i>residual redundancy</i> – can be calculated from | |
| − | * | + | * the length $N$ of the input sequence, |
| − | * | + | * the length $L(N)$ of the output sequence and |
| − | * | + | *the entropy $H$ |
| − | in | + | can be calculated in the following way: |
:$$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$ | :$$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$ | ||
| − | + | This takes into account that with perfect source coding the length of the output sequence could be lowered to the value $L_{\rm min} = N · H$ . | |
| − | * | + | *With non-perfect source coding, $L(n) - N · H$ gives the remaining redundancy (with the pseudo–unit "bit"). |
| − | * | + | *After dividing by $L(n)$ , one obtains the relative redundancy $r(n)$ with the value range between zero and one; $r(n)$ should be as small as possible. |
| − | + | A second parameter for measuring the efficiency of LZW coding is the <i>compression factor</i> $K(N)$, which should also be small as the quotient of the lengths of the output and input sequences: | |
| + | |||
:$$K(N) = {L(N) }/{N} \hspace{0.05cm},$$ | :$$K(N) = {L(N) }/{N} \hspace{0.05cm},$$ | ||
| − | + | In the [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Quantitative_statements_on_asymptotic_optimality|theory section]] it was shown that the residual redundancy $r(n)$ is often given by the function | |
:$$r\hspace{0.05cm}'(N) =\frac {A}{{\rm lg}\hspace{0.1cm}(N)} | :$$r\hspace{0.05cm}'(N) =\frac {A}{{\rm lg}\hspace{0.1cm}(N)} | ||
\hspace{0.5cm}{\rm mit}\hspace{0.5cm} A = 4 \cdot {r(N = 10000)} | \hspace{0.5cm}{\rm mit}\hspace{0.5cm} A = 4 \cdot {r(N = 10000)} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | + | is well approximated. | |
| − | * | + | *This approximation $r\hspace{0.05cm}'(N)$ is given for $\rm BQ1$ in the second column of the table above. |
| − | * In | + | * In subtasks '''(4)''' and '''(5)''' you are to make the approximation for sources $\rm BQ2$ and $\rm BQ3$ . |
| Line 53: | Line 54: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *The task belongs to the chapter [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch|Compression according to Lempel, Ziv and Welch]]. |
| − | * | + | *In particular, reference is made to the pages |
| − | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch# | + | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Remaining_redundancy_as_a_measure_for_the_efficiency_of_coding_methods|Residual redundancy as a measure for the efficiency of coding methods]], |
| − | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch# | + | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Efficiency_of_Lempel-Ziv_coding|Efficiency of Lempel-Ziv coding]] and |
| − | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch# | + | :: [[Information_Theory/Komprimierung_nach_Lempel,_Ziv_und_Welch#Quantitative_statements_on_asymptotic_optimality|Quantitative statements on asymptotic optimality]]. |
| − | * | + | *The descriptive variables $K(N)$ and $r(N)$ are deterministically related. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {With which parameter $A$ was the approximation $r\hspace{0.05cm}'(N)$ of the residual redundancy for the binary source $\rm BQ1$ created? |
|type="{}"} | |type="{}"} | ||
$A \ = \ $ { 1.06 3% } | $A \ = \ $ { 1.06 3% } | ||
| − | { | + | {What is the minimum size of $N = N_2$ for $\rm BQ1$ so that the residual redundancy satisfies the condition $r(N) ≈ r\hspace{0.05cm}'(N) \le 5\%$ ? |
|type="{}"} | |type="{}"} | ||
$N_{2} \ = \ $ { 1.58 3% } $\ \cdot 10^{21}$ | $N_{2} \ = \ $ { 1.58 3% } $\ \cdot 10^{21}$ | ||
| − | { | + | {What is the minimum size of $N = N_3$ at $\rm BQ1$ so that the compression factor $K(N)= L(N)/N$ is not greater than $0.6$? |
|type="{}"} | |type="{}"} | ||
$N_{3} \ = \ $ { 2.29 3% } $\ \cdot 10^{6}$ | $N_{3} \ = \ $ { 2.29 3% } $\ \cdot 10^{6}$ | ||
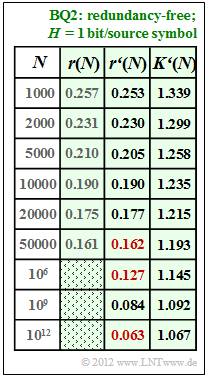
| − | { | + | {Now determine the redundancy approximation $r\hspace{0.05cm}'(N)$ for the redundancy-free binary source $\rm BQ2$, in particular: |
|type="{}"} | |type="{}"} | ||
$r'(N = 50000)\ = \ $ { 0.162 3% } | $r'(N = 50000)\ = \ $ { 0.162 3% } | ||
| Line 88: | Line 89: | ||
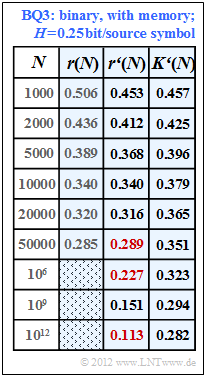
| − | { | + | {What values does the redundancy approximation $r\hspace{0.05cm}'(N)$ yield for the unspecified binary source $\rm BQ3$? In particular: |
|type="{}"} | |type="{}"} | ||
$r'(N = 50000)\ = \ $ { 0.289 3% } | $r'(N = 50000)\ = \ $ { 0.289 3% } | ||
| Line 95: | Line 96: | ||
| − | { | + | {According to this result, what source entropy $H$ could $\rm BQ3$ ? <i>Hint:</i> Exactly one answer is correct. |
|type="()"} | |type="()"} | ||
| − | - $H = 1.00 \ \rm bit/ | + | - $H = 1.00 \ \rm bit/source symbol$, |
| − | - $H = 0.75 \ \rm bit/ | + | - $H = 0.75 \ \rm bit/source symbol$, |
| − | - $H = 0.50 \ \rm bit/ | + | - $H = 0.50 \ \rm bit/source symbol$, |
| − | + $H = 0.25 \ \rm bit/ | + | + $H = 0.25 \ \rm bit/source symbol$. |
| Line 106: | Line 107: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Die Näherung $r\hspace{0.05cm}'(N)$ stimmt per Definition für die Folgenlänge $N = 10000$ mit der per Simulation ermittelten Restredundanz $r(N) = 0.265$ exakt überein. | '''(1)''' Die Näherung $r\hspace{0.05cm}'(N)$ stimmt per Definition für die Folgenlänge $N = 10000$ mit der per Simulation ermittelten Restredundanz $r(N) = 0.265$ exakt überein. | ||
Revision as of 19:03, 31 July 2021
We assume here a binary input sequence of length $N$ and consider three different binary message sources:
- $\rm BQ1$: Symbol probabilities $p_{\rm A} = 0.89$ and $p_{\rm B} = 0.11$, i.e. different
⇒ entropy $H = 0.5\text{ bit/source symbol}$ ⇒ the source is redundant. - $\rm BQ2$: $p_{\rm A} = p_{\rm B} = 0.5$ (equally probable)
⇒ entropy $H = 1\text{ bit/source symbol}$ ⇒ the source is redundancy-free. - $\rm BQ3$: There is no concrete information on the statistics here.
In subtask (6) you are to estimate the entropy $H$ of this source.
For these three sources, the respective residual redundancy $r(N)$ was determined by simulation, which remains in the binary sequence after Lempel–Ziv–Welch–coding in der Binärfolge verbleibt.
The results are shown in the first column of the above table for the sources
- $\rm BQ1$ (yellow background),
- $\rm BQ2$ (green background) and
- $\rm BQ3$ (blue background)
whereby we have restricted ourselves to sequence lengths $N ≤ 50000$ in the simulation.
The relative redundancy of the output sequence – simplified called residual redundancy – can be calculated from
- the length $N$ of the input sequence,
- the length $L(N)$ of the output sequence and
- the entropy $H$
can be calculated in the following way:
- $$r(N) = \frac{L(N) - N \cdot H}{L(N)}= 1 - \frac{ N \cdot H}{L(N)}\hspace{0.05cm}.$$
This takes into account that with perfect source coding the length of the output sequence could be lowered to the value $L_{\rm min} = N · H$ .
- With non-perfect source coding, $L(n) - N · H$ gives the remaining redundancy (with the pseudo–unit "bit").
- After dividing by $L(n)$ , one obtains the relative redundancy $r(n)$ with the value range between zero and one; $r(n)$ should be as small as possible.
A second parameter for measuring the efficiency of LZW coding is the compression factor $K(N)$, which should also be small as the quotient of the lengths of the output and input sequences:
- $$K(N) = {L(N) }/{N} \hspace{0.05cm},$$
In the theory section it was shown that the residual redundancy $r(n)$ is often given by the function
- $$r\hspace{0.05cm}'(N) =\frac {A}{{\rm lg}\hspace{0.1cm}(N)} \hspace{0.5cm}{\rm mit}\hspace{0.5cm} A = 4 \cdot {r(N = 10000)} \hspace{0.05cm}.$$
is well approximated.
- This approximation $r\hspace{0.05cm}'(N)$ is given for $\rm BQ1$ in the second column of the table above.
- In subtasks (4) and (5) you are to make the approximation for sources $\rm BQ2$ and $\rm BQ3$ .
Hints:
- The task belongs to the chapter Compression according to Lempel, Ziv and Welch.
- In particular, reference is made to the pages
- The descriptive variables $K(N)$ and $r(N)$ are deterministically related.
Questions
Solution
- Damit ist
- $$A = 4 \cdot r(N = 10000) =4 \cdot {0.265} \hspace{0.15cm}\underline{= 1.06} \hspace{0.05cm}. $$
(2) Aus der Beziehung ${A}/{\rm lg}\hspace{0.1cm}(N) ≤ 0.05$ ⇒ ${A}/{\rm lg}\hspace{0.1cm}(N) = 0.05$ folgt:
- $${{\rm lg}\hspace{0.1cm}N_{\rm 2}} = \frac{A}{0.05} = 21.2 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} N_{\rm 2} = 10^{21.2} \hspace{0.15cm}\underline{= 1.58 \cdot 10^{21}} \hspace{0.05cm}.$$
(3) Allgemein gilt $r(N) = 1 - {H}/{K(N)} \hspace{0.05cm}.$
- $\rm BQ1$ hat die Entropie $H = 0.5$ bit/Symbol.
- Daraus folgt wegen $r(N) ≈ r\hspace{0.05cm}'(N)$ für $K(N_3) = 0.6$:
- $$r(N_{\rm c}) = 1 - \frac{0.5}{0.6} = 0.167 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} {\rm lg}\hspace{0.1cm}N_{\rm 3} = \frac{A}{0.167} = 6.36 \hspace{0.1cm}\Rightarrow\hspace{0.1cm} N_{\rm 3} = 10^{6.36} \hspace{0.15cm}\underline{= 2.29 \cdot 10^{6}} \hspace{0.05cm}.$$
(4) Für $N = 10000$ gilt $r(N) ≈ r\hspace{0.05cm}'(N) = 0.19$:
- $$\frac{A}{{\rm lg}\hspace{0.1cm}10000} = 0.19 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} A = 0.19 \cdot 4 = 0.76 \hspace{0.05cm}. $$
- Die Ergebnisse sind in nebenstehender Tabelle zusammengefasst.
- Man erkennt die sehr gute Übereinstimmung zwischen $r(N)$ und $r\hspace{0.05cm}'(N)$.
- Die gesuchten Zahlenwerte sind in der Tabelle rot markiert:
$$r'(N = 50000)\hspace{0.15cm}\underline{ = 0.162},\hspace{0.3cm}r'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.127},\hspace{0.3cm} r'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.063}.$$
- Für den Komprimierungsfaktor gilt (der Apostroph weist darauf hin, dass von der Näherung $r\hspace{0.05cm}'(N)$ ausgegangen wurde):
- $$K\hspace{0.05cm}'(N) = \frac{1}{1 - r\hspace{0.05cm}'(N)}\hspace{0.05cm}.$$
- Damit gilt für die Länge des LZW–Ausgabestrings:
- $$L\hspace{0.05cm}'(N) = K\hspace{0.05cm}'(N) \cdot N = \frac{N}{1 - r\hspace{0.05cm}'(N)}\hspace{0.05cm}.$$
(5) Nach ähnlicher Vorgehensweise wie in der Teilaufgabe (4) erhält man für die Binärquelle $\rm BQ3$ den Anpassungsparameter $A = 1.36$ und daraus die Ergebnisse gemäß der blau hinterlegten Tabelle.
Hinweis: Die letzte Spalte dieser Tabelle ist nur bei Kenntnis der Teilaufgabe (6) verständlich. Dort wird gezeigt, dass die Quelle $\rm BQ3$ die Entropie $H = 0.25$ bit/Quellensymbol besitzt.
- In diesem Fall gilt für den Komprimierungsfaktor:
- $$K\hspace{0.05cm}'(N) = \frac{H}{1 - r\hspace{0.05cm}'(N)} = \frac{0.25}{1 - r'(N)} \hspace{0.05cm}.$$
- Damit erhält man für die gesuchten Werte der Restredundanz:
- $$r\hspace{0.05cm}'(N = 50000)\hspace{0.15cm}\underline{ = 0.289},\hspace{0.3cm}r\hspace{0.05cm}'(N = 10^{6})\hspace{0.15cm}\underline{ = 0.227},\hspace{0.3cm} r\hspace{0.05cm}'(N = 10^{12})\hspace{0.15cm}\underline{ = 0.113}.$$
- Für $N = 10^{12}$ weicht also der Komprimierungsfaktor $(0.282)$ noch deutlich von der Entropie $(0.25)$ ab, die erst für $N \to \infty$ erreicht werden kann (Quellencodierungstheorem).
(6) Die einzelnen Näherungen $r\hspace{0.05cm}'(N)$ unterscheiden sich nur durch den Parameter $A$. Dabei haben wir festgestellt:
- Quelle $\rm BQ1$ mit $H = 0.50$ ⇒ $A = 1.06$ ⇒ entsprechend dem Angabenblatt,
- Quelle $\rm BQ2$ mit $H = 1.00$ ⇒ $A = 0.76$ ⇒ siehe Teilaufgabe (4),
- Quelle $\rm BQ3$ $(H$ unbekannt$)$: $A = 4 · 0.34 =1.36$ ⇒ entsprechend der letzten Spalte in der Tabelle.
- Je kleiner die Entropie $H$ ist, um so größer ist offensichtlich der Anpassungsfaktor $A$ (und umgekehrt).
- Da genau eine Lösung möglich ist, muss $H = 0.25$ bit/Quellensymbol richtig sein ⇒ Antwort 4.
- Tatsächlich wurden bei der Simulation für die Quelle $\rm BQ3$ die Wahrscheinlichkeiten $p_{\rm A} = 0.96$ und $p_{\rm B} = 0.04$ ⇒ $H ≈ 0.25$ verwendet.