Difference between revisions of "Aufgaben:Exercise 2.6: About the Huffman Coding"
| Line 3: | Line 3: | ||
}} | }} | ||
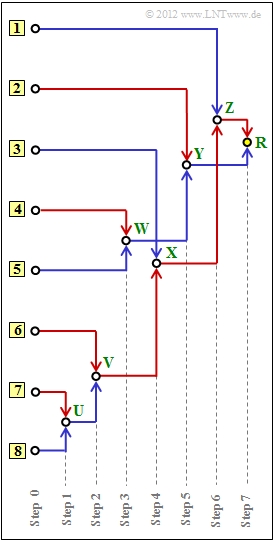
| − | [[File:EN_Inf_A_2_6_v2.png|right|frame|Tree diagram of the <br> | + | [[File:EN_Inf_A_2_6_v2.png|right|frame|Tree diagram of the <br>Huffman method]] |
We consider here a source symbol sequence $\langle q_\nu \rangle$ with symbol range $M = 8$: | We consider here a source symbol sequence $\langle q_\nu \rangle$ with symbol range $M = 8$: | ||
:$$q_{\nu} = \{ \hspace{0.05cm}q_{\mu} \} = \{ \boldsymbol{\rm A} \hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm B}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm C}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm D}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm E}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm F}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm G}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm H}\hspace{0.05cm} | :$$q_{\nu} = \{ \hspace{0.05cm}q_{\mu} \} = \{ \boldsymbol{\rm A} \hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm B}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm C}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm D}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm E}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm F}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm G}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm H}\hspace{0.05cm} | ||
\}\hspace{0.05cm}.$$ | \}\hspace{0.05cm}.$$ | ||
| − | If the symbols are equally probable, i.e. $p_{\rm A} = p_{\rm B} =$ ... $ = p_{\rm H} = 1/M$then source coding makes no sense. Already with the dual code $\rm A$ → <b>000</b>, $\rm B$ → <b>001</b>, ... , $\rm H$ → <b>111</b>, the mean codeword length $L_{\rm M}$ | + | If the symbols are equally probable, i.e. $p_{\rm A} = p_{\rm B} =$ ... $ = p_{\rm H} = 1/M$ then source coding makes no sense. Already with the dual code $\rm A$ → <b>000</b>, $\rm B$ → <b>001</b>, ... , $\rm H$ → <b>111</b>, the mean codeword length $L_{\rm M}$ is its lower bound $H$ according to the source coding theorem $(H$ denotes the <i>source entropy</i>$ here)$: |
| − | :$$L_{\rm M,\hspace{0.08cm}min} = H = 3 \hspace{0.15cm}{\rm bit/ | + | :$$L_{\rm M,\hspace{0.08cm}min} = H = 3 \hspace{0.15cm}{\rm bit/source symbol} \hspace{0.05cm}.$$ |
| − | + | However, let the symbol probabilities in this task be given as follows: | |
:$$p_{\rm A} \hspace{-0.05cm}= \hspace{-0.05cm} 0.04 \hspace{0.05cm},\hspace{0.1cm}p_{\rm B} \hspace{-0.05cm}= \hspace{-0.05cm} 0.08 \hspace{0.05cm},\hspace{0.1cm}p_{\rm C} \hspace{-0.05cm}= \hspace{-0.05cm} 0.14 \hspace{0.05cm},\hspace{0.1cm} | :$$p_{\rm A} \hspace{-0.05cm}= \hspace{-0.05cm} 0.04 \hspace{0.05cm},\hspace{0.1cm}p_{\rm B} \hspace{-0.05cm}= \hspace{-0.05cm} 0.08 \hspace{0.05cm},\hspace{0.1cm}p_{\rm C} \hspace{-0.05cm}= \hspace{-0.05cm} 0.14 \hspace{0.05cm},\hspace{0.1cm} | ||
p_{\rm D} \hspace{-0.05cm}= \hspace{-0.05cm} 0.25 \hspace{0.05cm},\hspace{0.1cm} p_{\rm E} \hspace{-0.05cm}= \hspace{-0.05cm} 0.24 \hspace{0.05cm},\hspace{0.1cm}p_{\rm F} \hspace{-0.05cm}= \hspace{-0.05cm} 0.12 \hspace{0.05cm},\hspace{0.1cm}p_{\rm G} \hspace{-0.05cm}= \hspace{-0.05cm} 0.10 \hspace{0.05cm},\hspace{0.1cm} | p_{\rm D} \hspace{-0.05cm}= \hspace{-0.05cm} 0.25 \hspace{0.05cm},\hspace{0.1cm} p_{\rm E} \hspace{-0.05cm}= \hspace{-0.05cm} 0.24 \hspace{0.05cm},\hspace{0.1cm}p_{\rm F} \hspace{-0.05cm}= \hspace{-0.05cm} 0.12 \hspace{0.05cm},\hspace{0.1cm}p_{\rm G} \hspace{-0.05cm}= \hspace{-0.05cm} 0.10 \hspace{0.05cm},\hspace{0.1cm} | ||
p_{\rm H} \hspace{-0.05cm}= \hspace{-0.05cm} 0.03 \hspace{0.05cm}.$$ | p_{\rm H} \hspace{-0.05cm}= \hspace{-0.05cm} 0.03 \hspace{0.05cm}.$$ | ||
| − | * | + | *So here we have a redundant message source that can be compressed by Huffman coding. |
| − | * | + | *This algorithm was published by [https://en.wikipedia.org/wiki/David_A._Huffman David Albert Huffman] – shortly after Shannon's groundbreaking work on information theory – and allows the construction of optimal prefix-free codes. |
| − | + | The algorithm is given here without derivation and proof, whereby we restrict ourselves to binary codes ⇒ the code symbol sequence consists only of zeros and ones: | |
| − | :'''(1)''' | + | :'''(1)''' Order the symbols according to decreasing probabilities of occurrence. |
| − | :'''(2)''' | + | :'''(2)''' Combine the two least likely symbols into a new symbol. |
| − | :'''(3)''' | + | :'''(3)''' Repeat steps '''(1)''' and '''(2)''', until only two (combined) symbols remain. |
| − | :'''(4)''' | + | :'''(4)''' Binary code the more probable set of symbols with <b>1</b> , the other set with <b>0</b>. |
| − | :'''(5)''' | + | :'''(5)''' Step by step (from bottom to top) add <b>1</b> or <b>0</b> to the split partial codes. |
| − | + | This algorithm is often illustrated by a tree diagram. The diagram above shows this for the case at hand. | |
| − | + | You have the following tasks: | |
| − | :'''(a)''' | + | :'''(a)''' Assign the symbols $\rm A$, ... , $\rm H$ to the inputs labelled '''[1]''', ... , '''[8]''' . |
| − | :'''(b)''' | + | :'''(b)''' Determination of the sum probabilities $U$, ... , $Z$ and $R$ (<i>root</i>). |
| − | :'''(c)''' | + | :'''(c)''' Assignment of the symbols $\rm A$, ... , $\rm H$ to the corresponding Huffman binary sequences. A red connection corresponds to a <b>1</b>, a blue connection to a <b>0</b>. |
| − | + | You will notice that the mean codeword length is | |
:$$L_{\rm M} = \sum_{\mu = 1}^{M}\hspace{0.05cm} p_{\mu} \cdot L_{\mu} $$ | :$$L_{\rm M} = \sum_{\mu = 1}^{M}\hspace{0.05cm} p_{\mu} \cdot L_{\mu} $$ | ||
| − | + | for Huffman coding is only slightly larger than the source entropy $H$. IIn this equation, the following values apply to the present case: | |
*$M = 8$, $p_1 = p_{\rm A}$, ... , $p_8 = p_{\rm H}$. | *$M = 8$, $p_1 = p_{\rm A}$, ... , $p_8 = p_{\rm H}$. | ||
| − | * | + | *The respective number of bits of the code symbols for $\rm A$, ... , $\rm H$ is denoted by $L_1$, ... , $L_8$ . |
| Line 53: | Line 53: | ||
| − | '' | + | ''Hints:'' |
| − | * | + | *The exercise belongs to the chapter [[Information_Theory/Entropiecodierung_nach_Huffman|Entropy Coding according to Huffman]]. |
| − | * | + | *In particular, reference is made to the pages |
| − | ** [[Information_Theory/Entropiecodierung_nach_Huffman# | + | ** [[Information_Theory/Entropiecodierung_nach_Huffman#The_Huffman_algorithm|The Huffman algorithm]], |
| − | **[[Information_Theory/Entropiecodierung_nach_Huffman# | + | **[[Information_Theory/Entropiecodierung_nach_Huffman#Representation_of_the_Huffman_code_as_a_tree_diagram|Representation of the Huffman code as a tree diagram]]. |
| − | * | + | *To check your results, please refer to the interaction module [[Applets:Huffman-_und_Shannon-Fano-Codierung|Shannon–Fano– and Huffman–coding]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which inputs in the tree diagram stand for |
|type="{}"} | |type="{}"} | ||
| − | + | Input number $ \ = \ $ { 7 } ⇒ symbol $\rm A$ | |
| − | + | Input number $ \ = \ $ { 6 } ⇒ symbol $\rm B$ | |
| − | + | Input number $ \ = \ $ { 3 } ⇒ symbol $\rm C$ | |
| − | + | Input number $ \ = \ $ { 1 } ⇒ symbol $\rm D$ | |
| − | { | + | {What numerical values (probabilities) should be at the nodes in the tree diagram? |
|type="{}"} | |type="{}"} | ||
| − | + | Probability $ \ = \ $ { 0.07 1% } at node $\rm U$ | |
| − | + | Probability $ \ = \ $ { 0.15 1% } at node $\rm V$ | |
| − | + | Probability $ \ = \ $ { 0.22 1% } at node $\rm W$ | |
| − | + | Probability $ \ = \ $ { 0.29 1% } at node $\rm X$ | |
| − | + | Probability $ \ = \ $ { 0.46 1% } at node $\rm Y$ | |
| − | + | Probability $ \ = \ $ { 0.54 1% } at node $\rm Z$ | |
| − | + | Probability $ \ = \ $ { 1 1% } at $\rm root$ | |
| − | { | + | {Which binary codes (represented with zeros and ones) result for |
|type="{}"} | |type="{}"} | ||
| − | + | Binary code $ \ = \ $ { 11101 } ⇒ symbol $\rm A$ | |
| − | + | Binary code $ \ = \ $ { 1111 } ⇒ symbol $\rm B$ | |
| − | + | Binary code $ \ = \ $ { 110 } ⇒ symbol $\rm C$ | |
| − | + | Binary code $ \ = \ $ { 10 } ⇒ symbol $\rm D$ | |
| − | { | + | {What is the mean codeword length? |
|type="{}"} | |type="{}"} | ||
| − | $L_{\rm M} \ = \ $ { 2.73 3% } $\ \rm bit/ | + | $L_{\rm M} \ = \ $ { 2.73 3% } $\ \rm bit/source symbol$ |
| − | { | + | {What is the source entropy $H$? |
|type="()"} | |type="()"} | ||
| − | + $H = 2.71\ \rm bit/ | + | + $H = 2.71\ \rm bit/source symbol.$ |
| − | - $H = 2.75\ \rm bit/ | + | - $H = 2.75\ \rm bit/source symbol.$ |
| − | - $H = 3.00\ \rm bit/ | + | - $H = 3.00\ \rm bit/source symbol.$ |
| Line 108: | Line 108: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Vor dem Huffman–Algorithmus müssen die Symbole nach ihren Auftrittswahrscheinlichkeiten sortiert werden. | '''(1)''' Vor dem Huffman–Algorithmus müssen die Symbole nach ihren Auftrittswahrscheinlichkeiten sortiert werden. | ||
Revision as of 21:25, 2 August 2021
We consider here a source symbol sequence $\langle q_\nu \rangle$ with symbol range $M = 8$:
- $$q_{\nu} = \{ \hspace{0.05cm}q_{\mu} \} = \{ \boldsymbol{\rm A} \hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm B}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm C}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm D}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm E}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm F}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm G}\hspace{0.05cm},\hspace{0.05cm} \boldsymbol{\rm H}\hspace{0.05cm} \}\hspace{0.05cm}.$$
If the symbols are equally probable, i.e. $p_{\rm A} = p_{\rm B} =$ ... $ = p_{\rm H} = 1/M$ then source coding makes no sense. Already with the dual code $\rm A$ → 000, $\rm B$ → 001, ... , $\rm H$ → 111, the mean codeword length $L_{\rm M}$ is its lower bound $H$ according to the source coding theorem $(H$ denotes the source entropy$ here)$:
- $$L_{\rm M,\hspace{0.08cm}min} = H = 3 \hspace{0.15cm}{\rm bit/source symbol} \hspace{0.05cm}.$$
However, let the symbol probabilities in this task be given as follows:
- $$p_{\rm A} \hspace{-0.05cm}= \hspace{-0.05cm} 0.04 \hspace{0.05cm},\hspace{0.1cm}p_{\rm B} \hspace{-0.05cm}= \hspace{-0.05cm} 0.08 \hspace{0.05cm},\hspace{0.1cm}p_{\rm C} \hspace{-0.05cm}= \hspace{-0.05cm} 0.14 \hspace{0.05cm},\hspace{0.1cm} p_{\rm D} \hspace{-0.05cm}= \hspace{-0.05cm} 0.25 \hspace{0.05cm},\hspace{0.1cm} p_{\rm E} \hspace{-0.05cm}= \hspace{-0.05cm} 0.24 \hspace{0.05cm},\hspace{0.1cm}p_{\rm F} \hspace{-0.05cm}= \hspace{-0.05cm} 0.12 \hspace{0.05cm},\hspace{0.1cm}p_{\rm G} \hspace{-0.05cm}= \hspace{-0.05cm} 0.10 \hspace{0.05cm},\hspace{0.1cm} p_{\rm H} \hspace{-0.05cm}= \hspace{-0.05cm} 0.03 \hspace{0.05cm}.$$
- So here we have a redundant message source that can be compressed by Huffman coding.
- This algorithm was published by David Albert Huffman – shortly after Shannon's groundbreaking work on information theory – and allows the construction of optimal prefix-free codes.
The algorithm is given here without derivation and proof, whereby we restrict ourselves to binary codes ⇒ the code symbol sequence consists only of zeros and ones:
- (1) Order the symbols according to decreasing probabilities of occurrence.
- (2) Combine the two least likely symbols into a new symbol.
- (3) Repeat steps (1) and (2), until only two (combined) symbols remain.
- (4) Binary code the more probable set of symbols with 1 , the other set with 0.
- (5) Step by step (from bottom to top) add 1 or 0 to the split partial codes.
This algorithm is often illustrated by a tree diagram. The diagram above shows this for the case at hand.
You have the following tasks:
- (a) Assign the symbols $\rm A$, ... , $\rm H$ to the inputs labelled [1], ... , [8] .
- (b) Determination of the sum probabilities $U$, ... , $Z$ and $R$ (root).
- (c) Assignment of the symbols $\rm A$, ... , $\rm H$ to the corresponding Huffman binary sequences. A red connection corresponds to a 1, a blue connection to a 0.
You will notice that the mean codeword length is
- $$L_{\rm M} = \sum_{\mu = 1}^{M}\hspace{0.05cm} p_{\mu} \cdot L_{\mu} $$
for Huffman coding is only slightly larger than the source entropy $H$. IIn this equation, the following values apply to the present case:
- $M = 8$, $p_1 = p_{\rm A}$, ... , $p_8 = p_{\rm H}$.
- The respective number of bits of the code symbols for $\rm A$, ... , $\rm H$ is denoted by $L_1$, ... , $L_8$ .
Hints:
- The exercise belongs to the chapter Entropy Coding according to Huffman.
- In particular, reference is made to the pages
- To check your results, please refer to the interaction module Shannon–Fano– and Huffman–coding.
Questions
Solution
- Da die zwei unwahrscheinlichsten Symbole schon im ersten Schritt zusammengefasst werden, nehmen die Auftrittswahrscheinlichkeiten von oben nach unten ab
(in der Grafik zu dieser Musterlösung von links nach rechts). - Durch Vergleich mit dem Angabenblatt erhält man:
- Symbol $\rm A$: Eingang 7, Symbol $\rm B$: Eingang 6, Symbol $\rm C$: Eingang 3, Symbol $\rm D$: Eingang 1.
P_ID2452__Inf_A_2_6a.png
(2) Der Knoten $\rm R$ ist die Baumwurzel (Root). Dieser ist stets mit $\underline{R=1}$ belegt, unabhängig von den Auftrittswahrscheinlichkeiten.
Für die weiteren Werte gilt:
- Schritt 1: $p_{\rm U} = p_{\rm A} + p_{\rm H} = 0.04 + 0.03 \hspace{0.15cm}\underline{ =0.07}$,
- Schritt 2: $p_{\rm V} = p_{\rm U} + p_{\rm B} = 0.07 + 0.08 \hspace{0.15cm}\underline{ =0.15}$,
- Schritt 3: $p_{\rm W} = p_{\rm F} + p_{\rm G} = 0.12 + 0.10 \hspace{0.15cm}\underline{ =0.22}$,
- Schritt 4: $p_{\rm X} = p_{\rm V} + p_{\rm C} = 0.15 + 0.14 \hspace{0.15cm}\underline{ =0.29}$,
- Schritt 5: $p_{\rm Y} = p_{\rm W} + p_{\rm E} = 0.22 + 0.24 \hspace{0.15cm}\underline{ =0.46}$,
- Schritt 6: $p_{\rm Z} = p_{\rm X} + p_{\rm D} = 0.29 + 0.25 \hspace{0.15cm}\underline{ =0.54}$.
(3) Den Huffman–Code für das Symbol $\rm A$ erhält man, wenn man den Weg von der $\rm Root$ (gelber Punkt) zum Symbol $\rm A$ zurückverfolgt und jeder roten Verbindungslinie eine 1 zuordnet, jeder blauen eine 0.
- Symbol $\rm A$: rot–rot–rot–blau–rot → 11101,
- Symbol $\rm B$: rot–rot–rot–rot → 1111,
- Symbol $\rm C$: rot–rot–blau → 110,
- Symbol $\rm D$: rot–blau– → 10,
- Symbol $\rm E$: blau–rot → 01,
- Symbol $\rm F$: blau–blau–rot → 001,
- Symbol $\rm G$: blau–blau–blau → 000,
- Symbol $\rm H$: rot–rot–rot–blau–blau → 11100.
(4) Die Codierung unter Punkt (3) hat ergeben, dass
- die Symbole $\rm D$ und $\rm E$ mit zwei Bit,
- die Symbole $\rm C$, $\rm F$ und $\rm G$ mit drei Bit,
- das Symbol $\rm B$ mit vier Bit, und
- die Symbole $\rm A$ und $\rm H$ jeweils mit fünf Bit
dargestellt werden. Damit erhält man für die mittlere Codewortlänge (in "bit/Quellensymbol&dquo;):
- $$L_{\rm M} \hspace{0.2cm} = \hspace{0.2cm} (p_{\rm D} + p_{\rm E}) \cdot 2 + (p_{\rm C} + p_{\rm F} + p_{\rm G}) \cdot 3 + p_{\rm B} \cdot 4 +(p_{\rm A} + p_{\rm H}) \cdot 5 = 0.49 \cdot 2 + 0.36 \cdot 3 +0.08 \cdot 4 +0.07 \cdot 5 \hspace{0.15cm}\underline{= 2.73}\hspace{0.05cm}.$$
(5) Richtig ist allein die Antwort 1:
- Die mittlere Codewortlänge $L_{\rm M}$ kann nicht kleiner sein als die Quellenentropie $H$. Damit scheiden die Antworten 2 und 3 aus.
- Aus den vorgegebenen Auftrittswahrscheinlichkeiten kann die Quellenentropie tatsächlich zu $H = 2.71$ bit/Quellensymbol berechnet werden.
- Man erkennt, dass diese Huffman–Codierung die vorgegebene Grenze (Quellencodierungstheorem) $L_{\rm M, \ min } \ge H = 2.71$ bit/Quellensymbol nahezu erreicht.