Difference between revisions of "Aufgaben:Exercise 4.6: AWGN Channel Capacity"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Information_Theory/AWGN_Channel_Capacity_for_Continuous_Input |
}} | }} | ||
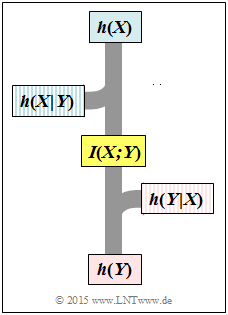
| − | [[File:P_ID2899__Inf_A_4_6.png|right|frame| | + | [[File:P_ID2899__Inf_A_4_6.png|right|frame|Flowchart of the information]] |
| − | + | We start from the [[Information_Theory/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang#Channel_capacity_of_the_AWGN_channel| AWGN channel model]] : | |
| − | * $X$ | + | * $X$ denotes the input (transmitter). |
| − | * $N$ | + | * $N$ stands for a Gaussian distributed noise. |
| − | * $Y = X +N$ | + | * $Y = X +N$ describes the output (receiver) in case of additive noise. |
| − | + | For the probability density function of the noise, let hold: | |
| − | |||
:$$f_N(n) = \frac{1}{\sqrt{2\pi \hspace{0.03cm}\sigma_{\hspace{-0.05cm}N}^2}} \cdot {\rm e}^{ | :$$f_N(n) = \frac{1}{\sqrt{2\pi \hspace{0.03cm}\sigma_{\hspace{-0.05cm}N}^2}} \cdot {\rm e}^{ | ||
- \hspace{0.05cm}{n^2}\hspace{-0.05cm}/{(2 \hspace{0.03cm} \sigma_{\hspace{-0.05cm}N}^2) }} \hspace{0.05cm}.$$ | - \hspace{0.05cm}{n^2}\hspace{-0.05cm}/{(2 \hspace{0.03cm} \sigma_{\hspace{-0.05cm}N}^2) }} \hspace{0.05cm}.$$ | ||
| − | + | Since the random variable $N$ is zero mean ⇒ $m_{N} = 0$, , we can equate the variance $\sigma_{\hspace{-0.05cm}N}^2$ with the power $P_N$ . In this case, the differential entropy of the random variable $N$ is specifiable (with the pseudo–unit "bit") as follows: | |
:$$h(N) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot P_N \right )\hspace{0.05cm}.$$ | :$$h(N) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot P_N \right )\hspace{0.05cm}.$$ | ||
| − | In | + | In this exercise, $P_N = 1 \rm mW$ is given. It should be noted: |
| − | * | + | * The power $P_N$ in the above equation, like the variance $\sigma_{\hspace{-0.05cm}N}^2$ , must be dimensionless. |
| − | * | + | * To work with this equation, the physical quantity $P_N$ must be suitably normalized, for example corresponding to $P_N = 1 \rm mW$ ⇒ $P_N\hspace{0.01cm}' = 1$. |
| − | * | + | * With other normalization, for example $P_N = 1 \rm mW$ ⇒ $P_N\hspace{0.01cm}' = 0.001$ a completely different numerical value would result fo $h(N)$ . |
| − | + | Further, you can consider for the solution of this exercise: | |
| − | * | + | * The channel capacitance is defined as the maximum transinformation between input $X$ and output $Y$ with the best possible input distribution: |
:$$C = \max_{\hspace{-0.15cm}f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.2cm} I(X;Y) | :$$C = \max_{\hspace{-0.15cm}f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.2cm} I(X;Y) | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | * | + | *The channel capacity of the AWGN channel is: |
:$$C_{\rm AWGN} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{P_N} \right ) | :$$C_{\rm AWGN} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{P_N} \right ) | ||
= {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_{\hspace{-0.05cm}X}\hspace{0.01cm}'}{P_{\hspace{-0.05cm}N}\hspace{0.01cm}'} \right )\hspace{0.05cm}.$$ | = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_{\hspace{-0.05cm}X}\hspace{0.01cm}'}{P_{\hspace{-0.05cm}N}\hspace{0.01cm}'} \right )\hspace{0.05cm}.$$ | ||
| − | : | + | :It can be seen: the channel capacity $C$ and also the mutual information $I(X; Y)$ are independent of the above normalization, in contrast to the differential entropies. |
| − | * | + | * With Gaussian noise PDF $f_N(n)$ , an input PDF $f_X(x)$ , also Gaussian, leads to the maximum transinformation and thus to the channel capacity. |
| Line 46: | Line 45: | ||
| − | + | Hints: | |
| − | * | + | *The task belongs to the chapter [[Information_Theory/AWGN–Kanalkapazität_bei_wertkontinuierlichem_Eingang|AWGN channel capacity with continuous-value input]]. |
| − | * | + | *Since the results are to be given in "bit", "log" ⇒ "log<sub>2</sub>" is used in the equations. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What transmit power is required for $C = 2 \ \rm bit$ ? |
|type="{}"} | |type="{}"} | ||
$P_X \ = \ $ { 15 3% } $\ \rm mW$ | $P_X \ = \ $ { 15 3% } $\ \rm mW$ | ||
| − | { | + | {Under which conditions is $I(X; Y) = 2 \ \rm bit$ achievable at all? |
|type="[]"} | |type="[]"} | ||
| − | + $P_X$ | + | + $P_X$ is determined as in '''(1)''' or larger. |
| − | + | + | + The random variable $X$ is Gaussian distributed. |
| − | + | + | + The random variable $X$ is zero mean. |
| − | + | + | + The random variables $X$ and $N$ are uncorrelated. |
| − | - | + | - The random variables $X$ and $Y$ are uncorrelated. |
| − | { | + | {Calculate the differential entropies of the random variables $N$, $X$ and $Y$ with appropriate normalization, <br>for example, $P_N = 1 \rm mW$ ⇒ $P_N\hspace{0.01cm}' = 1$. |
|type="{}"} | |type="{}"} | ||
$h(N) \ = \ $ { 2.047 3% } $\ \rm bit$ | $h(N) \ = \ $ { 2.047 3% } $\ \rm bit$ | ||
| Line 77: | Line 76: | ||
| − | { | + | {What are the other information-theoretic descriptive quantities? |
|type="{}"} | |type="{}"} | ||
$h(Y|X) \ = \ $ { 2.047 3% } $\ \rm bit$ | $h(Y|X) \ = \ $ { 2.047 3% } $\ \rm bit$ | ||
| Line 85: | Line 84: | ||
| − | { | + | {What quantities would result for the same $P_X$ in the limiting case $P_N\hspace{0.01cm} ' \to 0$ ? |
|type="{}"} | |type="{}"} | ||
$h(X) \ = \ $ { 4 3% } $\ \rm bit$ | $h(X) \ = \ $ { 4 3% } $\ \rm bit$ | ||
| Line 97: | Line 96: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The equation for the AWGN channel capacity in "bit" is: |
:$$C_{\rm bit} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right )\hspace{0.05cm}.$$ | :$$C_{\rm bit} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right )\hspace{0.05cm}.$$ | ||
| − | + | With $C_{\rm bit} = 2$ this results in: | |
:$$4 \stackrel{!}{=} {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right ) | :$$4 \stackrel{!}{=} {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right ) | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 1 + {P_X}/{P_N} \stackrel {!}{=} 2^4 = 16 | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 1 + {P_X}/{P_N} \stackrel {!}{=} 2^4 = 16 | ||
Revision as of 14:11, 1 October 2021
We start from the AWGN channel model :
- $X$ denotes the input (transmitter).
- $N$ stands for a Gaussian distributed noise.
- $Y = X +N$ describes the output (receiver) in case of additive noise.
For the probability density function of the noise, let hold:
- $$f_N(n) = \frac{1}{\sqrt{2\pi \hspace{0.03cm}\sigma_{\hspace{-0.05cm}N}^2}} \cdot {\rm e}^{ - \hspace{0.05cm}{n^2}\hspace{-0.05cm}/{(2 \hspace{0.03cm} \sigma_{\hspace{-0.05cm}N}^2) }} \hspace{0.05cm}.$$
Since the random variable $N$ is zero mean ⇒ $m_{N} = 0$, , we can equate the variance $\sigma_{\hspace{-0.05cm}N}^2$ with the power $P_N$ . In this case, the differential entropy of the random variable $N$ is specifiable (with the pseudo–unit "bit") as follows:
- $$h(N) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot P_N \right )\hspace{0.05cm}.$$
In this exercise, $P_N = 1 \rm mW$ is given. It should be noted:
- The power $P_N$ in the above equation, like the variance $\sigma_{\hspace{-0.05cm}N}^2$ , must be dimensionless.
- To work with this equation, the physical quantity $P_N$ must be suitably normalized, for example corresponding to $P_N = 1 \rm mW$ ⇒ $P_N\hspace{0.01cm}' = 1$.
- With other normalization, for example $P_N = 1 \rm mW$ ⇒ $P_N\hspace{0.01cm}' = 0.001$ a completely different numerical value would result fo $h(N)$ .
Further, you can consider for the solution of this exercise:
- The channel capacitance is defined as the maximum transinformation between input $X$ and output $Y$ with the best possible input distribution:
- $$C = \max_{\hspace{-0.15cm}f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.2cm} I(X;Y) \hspace{0.05cm}.$$
- The channel capacity of the AWGN channel is:
- $$C_{\rm AWGN} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_X}{P_N} \right ) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + \frac{P_{\hspace{-0.05cm}X}\hspace{0.01cm}'}{P_{\hspace{-0.05cm}N}\hspace{0.01cm}'} \right )\hspace{0.05cm}.$$
- It can be seen: the channel capacity $C$ and also the mutual information $I(X; Y)$ are independent of the above normalization, in contrast to the differential entropies.
- With Gaussian noise PDF $f_N(n)$ , an input PDF $f_X(x)$ , also Gaussian, leads to the maximum transinformation and thus to the channel capacity.
Hints:
- The task belongs to the chapter AWGN channel capacity with continuous-value input.
- Since the results are to be given in "bit", "log" ⇒ "log2" is used in the equations.
Questions
Solution
- $$C_{\rm bit} = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right )\hspace{0.05cm}.$$
With $C_{\rm bit} = 2$ this results in:
- $$4 \stackrel{!}{=} {\rm log}_2\hspace{0.05cm}\left ( 1 + {P_X}/{P_N} \right ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 1 + {P_X}/{P_N} \stackrel {!}{=} 2^4 = 16 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} P_X = 15 \cdot P_N \hspace{0.15cm}\underline{= 15\,{\rm mW}} \hspace{0.05cm}. $$
(2) Richtig sind die Lösungsvorschläge 1 bis 4. Begründung:
- Für $P_X < 15 \ \rm mW$ wird die Transinformation $I(X; Y)$ stets kleiner als $2$ bit sein, unabhängig von allen anderen Gegebenheiten.
- Mit $P_X = 15 \ \rm mW$ ist die maximale Transinformation $I(X; Y) = 2$ bit nur erreichbar, wenn die Eingangsgröße $X$ gaußverteilt ist.
Die Ausgangsgröße $Y$ ist dann ebenfalls gaußverteilt. - Weist die Zufallsgröße $X$ einen Gleichanteil $m_X$ auf, so ist die Varianz $\sigma_X^2 = P_X - m_X^2 $ bei gegebenem $P_X$ kleiner, und es gilt $I(X; Y) = 1/2 · \log_2 \ (1 + \sigma_X^2/P_N) < 2$ bit.
- Voraussetzung für die gegebene Kanalkapazitätsgleichung ist, dass $X$ und $N$ unkorreliert sind. Wären dagegen die Zufallsgrößen $X$ und $N$ unkorreliert, so ergäbe sich $I(X; Y) = 0$.
(3) Die angegebene Gleichung für die differentielle Entropie macht nur bei dimensionsloser Leistung Sinn. Mit der vorgeschlagenen Normierung erhält man:
- Für $P_N = 1 \ \rm mW$ ⇒ $P_N\hspace{0.05cm}' = 1$:
- $$h(N) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot 1 \right ) = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 17.08 \right ) \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm},$$
- Für $P_X = 15 \ \rm mW$ ⇒ $P_X\hspace{0.01cm}' = 15$:
- $$h(X) \ = \ {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \cdot 15 \right ) = {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left ( 2\pi {\rm e} \right ) + {1}/{2} \cdot {\rm log}_2\hspace{0.05cm}\left (15 \right ) \hspace{0.15cm}\underline{= 4.000\,{\rm bit}}\hspace{0.05cm}, $$
- Für $P_Y = P_X + P_N = 16 \ \rm mW$ ⇒ $P_Y\hspace{0.01cm}' = 16$:
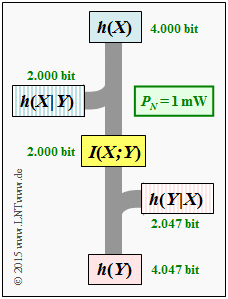
- $$h(Y) = 2.047\,{\rm bit} + 2.000\,{\rm bit} \hspace{0.15cm}\underline{= 4.047\,{\rm bit}}\hspace{0.05cm}.$$
(4) Für die differentielle Irrelevanz gilt beim AWGN–Kanal:
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(N) \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}.$$
- Entsprechend nebenstehender Grafik gilt aber auch:
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) = h(Y) - I(X;Y) = 4.047 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 2.047\,{\rm bit}}\hspace{0.05cm}. $$
- Daraus kann die differentielle Äquivokation wie folgt berechnet werden:
- $$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = h(X) - I(X;Y) = 4.000 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 2.000\,{\rm bit}}\hspace{0.05cm}.$$
- Abschließend wird auch noch die differentielle Verbundentropie angegeben, die aus obigem Schaubild nicht direkt ablesbar ist:
- $$h(XY) = h(X) + h(Y) - I(X;Y) = 4.000 \,{\rm bit} + 4.047 \,{\rm bit} - 2 \,{\rm bit} \hspace{0.15cm}\underline{= 6.047\,{\rm bit}}\hspace{0.05cm}.$$
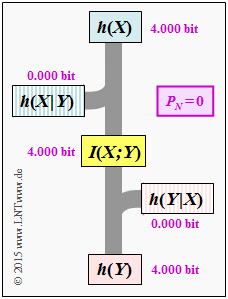
(5) Beim idealen Kanal erhält man mit $h(X)\hspace{0.15cm}\underline{= 4.000 \,{\rm bit}}$:
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) \ = \ h(N) \hspace{0.15cm}\underline{= 0\,{\rm (bit)}}\hspace{0.05cm},$$
- $$h(Y) \ = \ h(X) \hspace{0.15cm}\underline{= 4\,{\rm bit}}\hspace{0.05cm},$$
- $$I(X;Y) \ = \ h(Y) - h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X)\hspace{0.15cm}\underline{= 4\,{\rm bit}}\hspace{0.05cm},$$ $$ h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) \ = \ h(X) - I(X;Y)\hspace{0.15cm}\underline{= 0\,{\rm (bit)}}\hspace{0.05cm}.$$
- Die Grafik zeigt diese Größen in einem Flussdiagramm.
- Das gleiche Diagramm ergäbe sich auch im wertdiskreten Fall mit $M = 16$ gleichwahrscheinlichen Symbolen ⇒ $H(X)= 4.000 \,{\rm bit}$.
- Man müsste nur jedes $h$ durch ein $H$ ersetzen.