Difference between revisions of "Aufgaben:Exercise 2.7: Two-Way Channel once more"
| Line 122: | Line 122: | ||
\big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \big].$$ | \big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \big].$$ | ||
| − | * | + | *The complex exponential functions can be converted using the [[Signal_Representation/Calculating_With_Complex_Numbers#Representation_by_magnitude_and_phase|Euler theorem]] as follows: |
:$${\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} | :$${\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} | ||
\big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \big] = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} | \big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \big] = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} | ||
\cdot \big[ {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} \big] = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \cdot 2 \cos(\pi f T) .$$ | \cdot \big[ {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} \big] = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \cdot 2 \cos(\pi f T) .$$ | ||
| − | * | + | *Hence, the following can be formulated for the output spectrum: |
:$$Y_1(f) = Y_{11}(f) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} | :$$Y_1(f) = Y_{11}(f) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} | ||
, \; \; {\rm mit } \; \; | , \; \; {\rm mit } \; \; | ||
| Line 133: | Line 133: | ||
f T} = 2T \cdot \frac {\sin(2\pi f T) }{2\pi f T}.$$ | f T} = 2T \cdot \frac {\sin(2\pi f T) }{2\pi f T}.$$ | ||
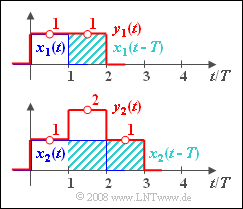
| − | [[File:P_ID925__LZI_A_2_7_a.png|right|frame| | + | [[File:P_ID925__LZI_A_2_7_a.png|right|frame|Input and output signals]] |
| − | + | Here, the relation $\sin(\alpha) \cdot \cos(\alpha) = \sin(2\alpha)/2$ is used. | |
| − | * | + | *The inverse Fourier transform of $Y_{11}$ results in a rectangle symmetric about $t = 0$ and of width $2T$. |
*Durch die Phasenfunktion wird dieser in den Bereich $0$ ... $2T$ verschoben und das Ergebnis der Zeitbereichsberechnung bestätigt. | *Durch die Phasenfunktion wird dieser in den Bereich $0$ ... $2T$ verschoben und das Ergebnis der Zeitbereichsberechnung bestätigt. | ||
| − | + | Despite the fact that $y_1(t)$ is rectangular just as $x_1(t)$, there are distortions: | |
*Wegen $T_y > T_x$ sind diese linear. Im interessierenden Frequenzbereich $($das sind bei einem si–förmigem Spektrum alle Frequenzen$)$ ist $|H(f)|$ nicht konstant. Also gibt es Dämpfungsverzerrungen. | *Wegen $T_y > T_x$ sind diese linear. Im interessierenden Frequenzbereich $($das sind bei einem si–förmigem Spektrum alle Frequenzen$)$ ist $|H(f)|$ nicht konstant. Also gibt es Dämpfungsverzerrungen. | ||
*Da zudem die Phase nicht im gesamten Bereich linear mit $f$ ansteigt, gibt es auch Phasenverzerrungen ⇒ Richtig sind die <u> Lösungsvorschläge 1, 3, 4 und 5</u>. | *Da zudem die Phase nicht im gesamten Bereich linear mit $f$ ansteigt, gibt es auch Phasenverzerrungen ⇒ Richtig sind die <u> Lösungsvorschläge 1, 3, 4 und 5</u>. | ||
Revision as of 21:59, 20 September 2021
As in Exercise 2.6, a two-way channel is considered whose impulse response is:
- $$h(t) = \delta ( t - T_1) + \delta ( t - T_2).$$
In contrast to the general representation in task 2.6, the two attenuation factors are equal here: $z_1 = z_2 = 1$.
- For mobile communications, this corresponds to an echo at a distance of $T_2 - T_1$ and of the same strength as the signal on the main path, for example.
- For this, the transit time $T_1$ is assumed.
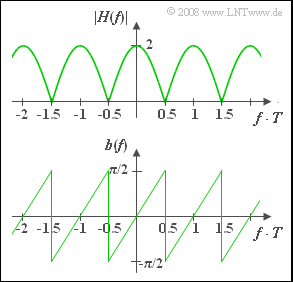
Using the transit times $T_1 = 0$ and $T_2 = T = 4 \ \rm ms$ considered in the subtasks (1) ... (4), the following is obtained for the frequency response of the two-way channel, whose magnitude is depicted in the upper graph:
- $$H(f) = 1 + {\rm e}^{-{\rm j}\hspace{0.04cm}2 \pi f T} = 1 + \cos(2 \pi f T) - {\rm j} \cdot \sin(2 \pi f T)$$
- $$\Rightarrow \hspace{0.4cm}|H(f)| = \sqrt{2\left(1 + \cos(2 \pi f T)\right)}= 2 \cdot |\cos(\pi f T)|.$$
The bottom graph shows the phase function:
- $$b(f) = - {\rm arc} \hspace{0.1cm}H(f) = \arctan \frac{\sin(2 \pi f T)}{1 + \cos(2 \pi f T)} = \arctan \big[\tan(\pi f T)\big].$$
The following trigonometric transformation was used here:
- $$ \frac{\sin(2 \alpha)}{1 + \cos(2 \alpha)} = \tan(\alpha).$$
The bottom graph shows thep hase function for $T_1 = 0$ and $T_2 = T = 4 \ \rm ms$:
- In the frequency range $|f| < 1/(2T)$, $b(f)$ increases linearly: $b(f) = \pi \cdot f \cdot T.$
- Also in further sections of the phase function, the phase always increases linearly from $-\pi/2$ to $+\pi/2$ .
In the questions, $y_i(t)$ denotes the signal at the output of the two-way channel if the signal $x_i(t)$ is applied to the input $( i = 1, 2, 3, 4)$.
These signals are examined as input signals:
- a rectangular pulse $x_1(t)$ with height $1$ between $t= 0$ and $t= T$;
$x_1(t) = 0$ holds for $t < 0$ and $t > T$ $($the value$0.5$ occurs at the two jump discontinuities, respectively$)$; - a rectangular pulse $x_2(t)$ with height $1$ in the range of $0 \ \text{...} \ 2T$;
- a periodic rectangular pulse $x_3(t)$ with period $T = T_0$:
- $$x_3(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} { 0 < t < T/2,} \\ { T/2 < t < T,} \\ \end{array}$$
- a periodic rectangular pulse $x_4(t)$ with period $T = 2T_0$:
- $$x_4(t) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} { 0 < t < T,} \\ { T < t < 2T.} \\ \end{array}$$
Please note:
- The task belongs to the chapter Linear Distortions.
- For subtasks (1) to (4), $T_1 = 0$ and $T_2 = T = 4 \ \rm ms$ hold.
- In subtask (5), the case $T_1 = 1 \ \rm ms$ and $T_2 = 5 \ \rm ms$ is considered.
Questions
Solution
- $$y_1(t) = x_1(t) \star h(t) = x_1(t) \star \delta (t) + x_1(t) \star \delta (t - T) = x_1(t) + x_1(t-T).$$
- Thus, $y_1(t)$ is a rectangular pulse of height $1$ and width $2T$.
- The same result – but in a more time-consuming way – is obtained by computing in the spectral domain:
- $$Y_1(f) = X_1(f) \cdot H(f) = T \cdot \frac {\sin(\pi f T)}{\pi f T}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} \cdot \big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \big].$$
- The complex exponential functions can be converted using the Euler theorem as follows:
- $${\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} \big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \big] = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \cdot \big[ {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \pi f T} \big] = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \cdot 2 \cos(\pi f T) .$$
- Hence, the following can be formulated for the output spectrum:
- $$Y_1(f) = Y_{11}(f) \cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} , \; \; {\rm mit } \; \; Y_{11}(f) = 2T \cdot \frac {\sin(\pi f T) \cdot \cos(\pi f T)}{\pi f T} = 2T \cdot \frac {\sin(2\pi f T) }{2\pi f T}.$$
Here, the relation $\sin(\alpha) \cdot \cos(\alpha) = \sin(2\alpha)/2$ is used.
- The inverse Fourier transform of $Y_{11}$ results in a rectangle symmetric about $t = 0$ and of width $2T$.
- Durch die Phasenfunktion wird dieser in den Bereich $0$ ... $2T$ verschoben und das Ergebnis der Zeitbereichsberechnung bestätigt.
Despite the fact that $y_1(t)$ is rectangular just as $x_1(t)$, there are distortions:
- Wegen $T_y > T_x$ sind diese linear. Im interessierenden Frequenzbereich $($das sind bei einem si–förmigem Spektrum alle Frequenzen$)$ ist $|H(f)|$ nicht konstant. Also gibt es Dämpfungsverzerrungen.
- Da zudem die Phase nicht im gesamten Bereich linear mit $f$ ansteigt, gibt es auch Phasenverzerrungen ⇒ Richtig sind die Lösungsvorschläge 1, 3, 4 und 5.
(2) Aufgrund der bereits in (1) angegebenen Gleichung
- $$y_2(t) = x_2(t) + x_2(t-T)$$
erhält man einen stufenförmigen Verlauf entsprechend dem unteren Diagramm der obere Grafik.
Die gesuchten Zahlenwerte sind: $y_2(t = 0.5 T) \hspace{0.15cm}\underline{= 1}, \hspace{0.3cm} y_2(t = 1.5 T) \hspace{0.15cm}\underline{= 2}, \hspace{0.3cm}y_2(t = 2.5 T) \hspace{0.15cm}\underline{ = 1}.$
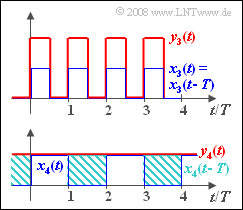
(3) Die Periodendauer $T_0 = T$ des periodischen Signals $x_3(t)$ ist genau so groß wie die Verzögerung auf dem zweiten Pfad. Deshalb ist $y_3(t) = 2 \cdot x_3(t) $ und es sind keine Verzerrungen feststellbar.
Die Spektralbereichsberechnung führt zum gleichen Ergebnis.
- $X_3(f)$ ist ein Linienspektrum mit Anteilen bei den Frequenzen $f = 0$, $f = \pm f_0 = \pm 1/T$, $f = \pm 3f_0$, usw..
- Bei diesen diskreten Frequenzen gilt aber exakt:
- $$|H(f)| = 2, \hspace{0.3cm} b(f) = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\tau_{\rm P}(f) = 0.$$
- Auch daraus folgt wieder $y_3(t) = 2 \cdot x_3(t) $.
- Richtig ist somit nur der Lösungsvorschlag 1.
(4) Aus der unteren Skizze der zweiten Grafik geht hervor, dass $y_4(t) = 1$ gegenüber $x_4(t)$ verzerrt ist. Dabei handelt es sich um Dämpfungsverzerrungen ⇒ Lösungsvorschlag 2, wie die folgende Überlegung zeigt.
- Wegen $T_0 = 2T$ weist das Signal $x_4(t)$ die Grundfrequenz $f_0 = 1/(2T)$ auf.
- Bei allen ungeraden Vielfachen von $f_0$ hat somit der Frequenzgang Nullstellen.
- Die einzige verbleibende Spektrallinie von $Y_4(f)$ liegt bei $f = 0$, wobei gilt:
- $$Y_4(f) = 2 \cdot 0.5 \cdot \delta (f) = 1 \cdot \delta (f) \hspace{0.5cm}\Rightarrow \hspace{0.5cm} y_4(t) = 1.$$
(5) Der Frequenzgang lautet nun mit $T_1 = 1 \ \rm ms$, $T_2 = 5 \ \rm ms$ und $T = T_2 -T_1 = 4 \ \rm ms$:
- $$H(f) = {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_1}+ {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_2}= \big[ 1 + {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T} \big]\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}2 \pi f T_1}.$$
- Der Klammerausdruck beschreibt den bereits bisher betrachteten Frequenzgang.
- Der zweite Term bewirkt eine zusätzliche Laufzeit um $ \tau = T_1$, und es gilt für alle Signale $(i = 1, 2, 3, 4)$:
- $$y_i^{\rm (5)}(t) = y_i(t-T_1).$$
Alle Aussagen hinsichtlich der Verzerrungen sind weiter gültig. Dies entspricht dem Lösungsvorschlag 1.