Difference between revisions of "Theory of Stochastic Signals/Set Theory Basics"
| Line 103: | Line 103: | ||
| − | [[File: | + | [[File:EN_Sto_T_1_2_S4Neu.png| right|frame|Complementary set in the Venn diagram]] |
In the Venn diagram, the complementary to $A$ is shaded. From this diagram, some set-theoretic relationships can be seen: | In the Venn diagram, the complementary to $A$ is shaded. From this diagram, some set-theoretic relationships can be seen: | ||
*The complementary of the complementary of $A$ is the set $A$ itself: | *The complementary of the complementary of $A$ is the set $A$ itself: | ||
Revision as of 16:46, 26 November 2021
Contents
Venn diagram, universal and empty set
In later chapters, we will sometimes refer to set theory . Therefore, the most important basics and definitions of this discipline will be briefly summarized here. The topic is also covered in the (German language) learning video
"Mengentheoretische Begriffe und Gesetzmäßigkeiten" ⇒ "Set Theory – Terms and Regularities"
An important tool of set theory is the Venn diagramm according to the graph:
- Applied to probability theory, here the events $A_i$ are represented as areas. For a simpler description we do not denote the events here with $A_1$, $A_2$ and $A_3$, but with $A$, $B$ and $C$ in contrast to the last chapter.
- The total area corresponds to the "universal set" (or short: "universe") $G$. The universe $G$ contains all possible outcomes and stands for the certain event, which by definition occurs with probability „one”: ${\rm Pr}(G) = 1$. For example, in the random experiment "Throwing a die", the probability for the event "The number of eyes is less than or equal to 6" is identical to one.
- In contrast, the empty set $ϕ$ does not contain a single element. In terms of events, the empty set specifies the impossible event with probability ${\rm Pr}(ϕ) = 0$ an. For example, in the experiment "Throwing a die", the probability for the event "The number of eyes is greater than 6" is identically zero.
Note that not every event $A$ with ${\rm Pr}(A) = 0$ can really never happen. For example:
- The event "The noise value $n$ is identically zero" is vanishingly small and ${\rm Pr}(n \equiv 0) = 0$, if $n$ is described by a continuous (Gaussian) random variable.
- Nevertheless, it is of course possible (although extremely unlikely) that at some point the exact noise value $n = 0$ will also occur.
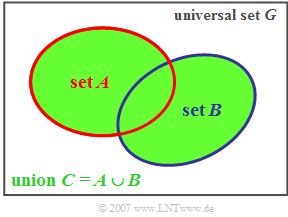
Union set
Some set-theoretical relationss are explained now on the basis of the Venn diagram.
$\text{Definition:}$ The union set $C$ of two sets $A$ and $B$ contains all the elements that are contained either in set $A$ or in set $B$ or in both.
- This relationship is expressed as the following formula:
- $$\ C = A \cup B.$$
Using the diagram, it is easy to see the following laws of set theory:
- $$A \cup \it \phi = A \rm \hspace{3.6cm}(union \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}empty \hspace{0.15cm}set),$$
- $$A\cup G = G \rm \hspace{3.6cm}(union \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}universe),$$
- $$A\cup A = A \hspace{3.6cm}(\rm tautology),$$
- $$A\cup B = B\cup A \hspace{2.75cm}(\rm commutative \hspace{0.15cm}property),$$
- $$(A\cup B)\cup C = A\cup (B\cup C) \hspace{0.45cm}(\rm associative \hspace{0.15cm}property).$$
If nothing else is known about the event sets $A$ and $B$ then only a lower bound and an upper bound can be given for the probability of the union set:
- $${\rm Max}\big({\rm Pr} (A), \ {\rm Pr} (B)\big) \le {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B).$$
- The probability of the union set is equal to the lower bound if $A$ is a subset of $B$ or vice versa.
- The upper bound holds for disjoint sets.
$\text{Example 1:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Consider the two events
- $A :=$ "The outcome is greater than or equal to $5$"$ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$,
- $B :=$ "The outcome is even" $= \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$,
then the union set contains four elements: $(A \cup B) = \{2, 4, 5, 6 \}$ ⇒ ${\rm Pr} (A \cup B) = 4/6 = 2/3$.
- For the lower bound: ${\rm Pr} (A \cup B) \ge {\rm Max}\big({\rm Pr} (A),\ {\rm Pr} (B)\big ) = 3/6.$
- For the upper bound: $ {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B) = 5/6.$
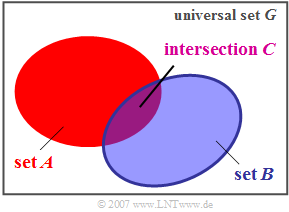
Intersection set
Another important set-theoretic relation is the intersection.
$\text{Definition:}$ The intersection set $C$ of two sets $A$ and $B$ contains all those elements which are contained in both the set $A$ and the set $B$.
- This relationship is expressed as the following formula:
- $$C = A \cap B.$$
In the diagram, the intersection is shown in purple. Analog to the union set, the following regularities apply here:
- $$A \cap \it \phi = \it \phi \rm \hspace{3.75cm}(intersection \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}empty \hspace{0.15cm}set),$$
- $$A \cap G = A \rm \hspace{3.6cm}(intersection \hspace{0.15cm}with \hspace{0.15cm}the \hspace{0.15cm}universe),$$
- $$A\cap A = A \rm \hspace{3.6cm}(tautology),$$
- $$A\cap B = B\cap A \rm \hspace{2.75cm}(commutative \hspace{0.15cm}property),$$
- $$(A\cap B)\cap C = A\cap (B\cap C) \rm \hspace{0.45cm}(associative \hspace{0.15cm}property).$$
- If nothing else is known about $A$ and $B$, then no statement can be made for the probability of the intersection.
- However, if ${\rm Pr} (A) \le 1/2$ and at the same time ${\rm Pr} (B) \le 1/2$ hold, then a lower and an upper bound can be given:
- $$0 \le {\rm Pr} (A ∩ B) \le {\rm Min}\ \big({\rm Pr} (A),\ {\rm Pr} (B)\big ).$$
- ${\rm Pr}(A ∩ B)$ is sometimes called the "joint probability" and is denoted by ${\rm Pr}(A, \ B)$.
- ${\rm Pr}(A ∩ B)$ is equal to the upper bound if $A$ is a subset of $B$ or vice versa.
- The lower bound is obtained for the joint probability of disjoint sets.
$\text{Example 2:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Consider the two events
- $A :=$ "The outcome is greater than or equal to $5$" $ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$, and
- $B :=$ "The outcome is even" $ = \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$.
The intersection contains only one element: $(A ∩ B) = \{ 6 \}$ ⇒ ${\rm Pr} (A ∩ B) = 1/6$.
- The upper bound is obtained as ${\rm Pr} (A ∩ B) \le {\rm Min}\ \big ({\rm Pr} (A), \, {\rm Pr} (B)\big ) = 2/6.$
- The lower bound of the intersection here is zero because of ${\rm Pr} (A) \le 1/2$ and ${\rm Pr} (B) \le 1/2$ .
Complementary set
$\text{Definition:}$ The complementary set of $A$ is often denoted by a straight line above the letter $(\overline{A})$ . It contains all the elements that are not contained in the set $A$ and it holds for their probability:
- $${\rm Pr}(\overline{A}) = 1- {\rm Pr}(A).$$
In the Venn diagram, the complementary to $A$ is shaded. From this diagram, some set-theoretic relationships can be seen:
- The complementary of the complementary of $A$ is the set $A$ itself:
- $$\overline{\overline{A}} = A.$$
- The union of a set $A$ with its complementary set gives the universal set:
- $${\rm Pr}(A \cup \overline{A}) = {\rm Pr}(G) = \rm 1.$$
- The intersection of $A$ with its complementary set gives the empty set:
- $${\rm Pr}(A \cap \overline{A}) = {\rm Pr}({\it \phi}) \rm = 0.$$
$\text{Example 3:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Starting from the set
- $A :=$ "The outcome is smaller than $5$" $= \{1, 2, 3, 4\}$ ⇒ ${\rm Pr} (A)= 2/3$,
the corresponding complementary set is
- $\overline{A} :=$ "The outcome is greater than or equal to $5$" $ = \{5, 6\}$ ⇒ ${\rm Pr} (\overline{A})= 1 - {\rm Pr} (A) = 1 - 2/3 = 1/3.$
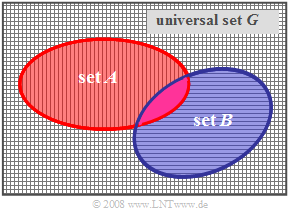
Proper subset – Improper subset
$\text{Definitions:}$
(1) One calls $A$ a proper subset of $B$ and writes for this relationship $A ⊂ B$,
- if all elements of $A$ are also contained in $B$,
- but not all elements of $B$ are contained in $A$.
In this case, the probabilities are:
- $${\rm Pr}(A) < {\rm Pr}(B).$$
This set-theoretic relationship is illustrated by the sketched Venn diagram on the right.
(2) On the other hand, $A$ is called an improper subset of $B$ and uses the notation
- $$A \subseteq B = (A \subset B) \cup (A = B),$$
if $A$ is either a proper subset of $B$ or if $A$ and $B$ are equal sets.
- The relation ${\rm Pr} (A) \le {\rm Pr} (B)$ then applies to the probabilities.
- The equality sign is only valid for the special case $A = B$.
In addition, however, the two equations known as the absorption laws also apply:
- $$(A \cap B) \cup A = A ,$$
- $$(A \cup B) \cap A = A,$$
since the intersection $A ∩ B$ is always a subset of $A$, but at the same time $A$ is also a subset of the union $A ∪ B$.
$\text{Example 4:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Consider the two events
- $A :=$ "The outcome is odd" $ = \{1, 3, 5\}$ ⇒ ${\rm Pr} (A)= 3/6$, and
- $B :=$ "The outcome is a prime number" $= \{1, 2, 3, 5\}$ ⇒ ${\rm Pr} (B)= 4/6$.
It can be seen that $A$ is a (proper) subset of $B$ . Accordingly, ${\rm Pr} (A) < {\rm Pr} (B)$ is also true.
Theorems of de Morgan
In many set-theoretical tasks, the two theorems of de Morgan are extremely useful. These are:
- $$\overline{A \cup B} = \overline{A} \cap \overline{B},$$
- $$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$
These regularities are illustrated in the Venn diagram:
- Set $A$ is shown in red and set $B$ is shown in blue.
- The compliment $\overline {A}$ of $A$ is hatched in the horizontal direction.
- The compliment $\overline {B}$ of $B$ is hatched in the vertical direction.
- The complement $\overline{A \cup B}$ of the union ${A \cup B}$ is hatched both horizontally and vertically.
- It is thus equal to the intersection $\overline{A} \cap \overline{B}$ of the two complement sets of $A$ and $B$:
- $$\overline{A \cup B} = \overline{A} \cap \overline{B}.$$
The second form of the de Morgan theorem can also be illustrated graphically with the same Venn diagram:
- The intersection $A ∩ B$ $($shown in purple in the figure$)$ is neither horizontally nor vertically hatched.
- Accordingly, the complement $\overline{A ∩ B}$ of the intersection is hatched either horizontally, vertically, or in both directions.
- By de Morgan's second theorem, the complement of the intersection equals the union of the two complementary sets of $A$ and $B$:
- $$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$
$\text{Example 5:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
We consider the two sets
- $A : =$ "The outcome is odd" $= \{1, 3, 5\}$,
- $B : =$ "The outcome is greater than $2$" $= \{3, 4, 5, 6\}$.
From this follow the two complementary sets
- $\overline {A} : =$ "The outcome is even" $= \{2, 4, 6\}$,
- $\overline {B} : =$ "The outcome is smaller than $3$" $= \{1, 2\}$.
Further, using the above theorems, we obtain the following sets:
- $$\overline{A \cup B} = \overline{A} \cap \overline{B} = \{2\},$$
- $$\overline{\it A \cap \it B} =\overline{\it A} \cup \overline{\it B} = \{1,2,4,6\}.$$
Disjoint sets
$\text{Definition:}$ Two sets $A$ and $B$ are called disjoint or incompatible,
- if there is no single element,
- that is contained in both $A$ and $B$.
The diagram shows two disjoint sets $A$ and $B$ in the Venn diagram.
In this special case, the following statements hold:
- The intersection of two disjoint sets $A$ and $B$ always yields the empty set:
- $${\rm Pr}(A \cap B) = {\rm Pr}(\phi) = \rm 0.$$
- The probability of the union set of two disjoint sets $A$ and $B$ is always equal to the sum of the two individual probabilities:
- $${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B).$$
$\text{Example 6:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
In our standard experiment, the two sets are now
- $A :=$ "The outcome is smaller than $3$" $ = \{1, 2\}$ ⇒ ${\rm Pr}( A) = 2/6$,
- $B :=$ "The outcome is greater than $3$" $ = \{4, 5,6\}$ ⇒ ${\rm Pr}( B) = 3/6$
disjoint to each other, since $A$ and $B$ do not contain a single common element.
- The intersection yields the empty set: ${A \cap B} = \phi$.
- The probability of the union set ${A \cup B} = \{1, 2, 4, 5, 6\}$ is equal to ${\rm Pr}( A) + {\rm Pr}(B) = 5/6.$
Addition rule
Only for disjoint sets $A$ and $B$, the relation ${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B)$ holds for the probability of the union set.
But how is this probability calculated for general events that are not necessarily disjoint?
Consider the right-hand Venn diagram with the intersection $A ∩ B$ shown in purple.
- The red set contains all the elements that belong to $A$, but not to $B$.
- The elements of $B$, that are not simultaneously contained in $A$ are shown in blue.
- All red, blue, and purple surfaces together make up the union set $A ∪ B$.
From this set-theoretic representation, one can see the following relationships:
- $${\rm Pr}(A) \hspace{0.8cm}= {\rm Pr}(A \cap B) + {\rm Pr}(A \cap \overline{B}),$$
- $${\rm Pr}(B) \hspace{0.8cm}= {\rm Pr}(A \cap B) \rm +{\rm Pr}(\overline{A} \cap {B}),$$
- $${\rm Pr}(A \cup B) ={\rm Pr}(A \cap B) +{\rm Pr} ({A} \cap \overline{B}) + {\rm Pr}(\overline{A} \cap {B}).$$
Adding the first two equations and subtracting from them the third, we get:
- $${\rm Pr}(A) +{\rm Pr}(B) -{\rm Pr}(A \cup B) = {\rm Pr}(A \cap B).$$
$\text{Definition:}$ By rearranging this equation, one arrives at the so-called Addition Rule for any two, not necessarily disjoint events:
- $${\rm Pr}(A \cup B) = {\rm Pr}(A) + {\rm Pr}(B) - {\rm Pr}(A \cap B).$$
$\text{Example 7:}$ We consider again the experiment "throwing a die". The possible outcomes (number of points) are thus $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
We consider the two sets
- $A :=$ "The outcome is odd" $= \{1, 3, 5\}$ ⇒ ${\rm Pr}(A) = 3/6$,
- $B :=$ "The outcome is greater than $2$" $ = \{3, 4, 5, 6\}$ ⇒ ${\rm Pr}(B) = 4/6$.
This gives the following probabilities
- of the union ⇒ ${\rm Pr}(A ∪ B) = 5/6$, and
- of the intersection ⇒ ${\rm Pr}(A ∩ B) = 2/6$.
The numerical values show the validity of the addition theorem: $5/6 = 3/6 + 4/6 − 2/6$.
Complete system
In the last section to this chapter, we consider again more than two possible events, namely, in general, $I$.
- These events will be denoted by $A_i$ ⇒ the running index $i$ can be in the range $1 ≤ i ≤ I$.
$\text{Definition:}$ A constellation with events $A_1, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_i, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_I$ is called a complete system, if and only if the following two conditions are satisfied:
(1) All events are pairwise disjoint:
- $$A_i \cap A_j = \it \phi \hspace{0.25cm}\rm for\hspace{0.15cm}all\hspace{0.25cm}\it i \ne j.$$
(2) The union of all event sets gives the universal set:
- $$\bigcup_{i=1}^{I} A_i = G.$$
Given these two assumptions, the sum of all probabilities is then:
- $$\sum_{i =1}^{ I} {\rm Pr}(A_i) = 1.$$
$\text{Example 8:}$
- The sets $A_1 := \{1, 5\}$ and $A_2 := \{2, 3\}$ together with the set $A_3 := \{4, 6\}$ result in a complete system in the random experiment "throwing a die",
- but not in the experiment "throwing a roulette ball".
$\text{Example 9:}$ Another example of a complete system is the discrete random variable $X = \{ x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ with the likelihood corresponding to the following probability mass function $\rm (PMF)$:
- $$P_X(X) = \big [ \hspace{0.1cm} P_X(x_1),\ P_X(x_2), \hspace{0.05cm}\text{...}\hspace{0.15cm},\ P_X(x_I) \hspace{0.05cm} \big ] = \big [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_I \hspace{0.05cm} \big ] \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm} p_1 = P_X(x_1) = {\rm Pr}(X=x_1) \hspace{0.05cm}, \hspace{0.2cm}p_2 = {\rm Pr}(X=x_2) \hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.15cm},\hspace{0.2cm} p_I = {\rm Pr}(X=x_I) \hspace{0.05cm}.$$
- The possible outcomes $x_i$ of the random variable $X$ are pairwise disjoint to each other.
- The sum of all likelihoods $p_1 + p_2 + \hspace{0.1cm}\text{...}\hspace{0.1cm} + \hspace{0.05cm} p_I$ always yields the result $1$.
$\text{Example 10:}$ Let $X= \{0, 1, 2 \}$ and $P_X (X) = \big[0.2, \ 0.5, \ 0.3\big]$. Then holds:
- $${\rm Pr}(X=0) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=1) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=2) = 0.3 \hspace{0.05cm}.$$
With random variable $X = \{1, \pi, {\rm e} \}$ and the same $P_X(X) = \big[0.2, \ 0.5, \ 0.3\big]$ the assignments are:
- $${\rm Pr}(X=1) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=\pi) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X={\rm e}) = 0.3 \hspace{0.05cm}.$$
Hints:
- The probability mass function $P_X(X)$ only makes statements about the probabilities, not about the set of values $\{x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ of the random variable $X$.
- This additional information is provided by the probability density function $\rm (PDF)$.
Exercises for the chapter
Exercise 1.2: Switching Logic (D/B Converter)
Exercise 1.3: Fictional University Somewhere
Exercise 1.3Z: Winning with Roulette?