Aufgaben:Exercise 1.2Z: Sets of Digits

• Return to book

Sets of digits  $A$,  $B$,  $C$

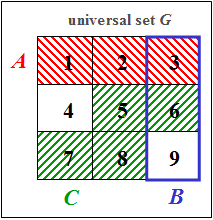
Let the universal set  $G$  be the set of all digits between  $1$  and  $9$.  Given are the following subsets:

$$A = \big[\text{digits} \leqslant 3\big],$$

$$ B = \big[\text{digits divisible by 3}\big],$$

$$ C = \big[\text{digits 5, 6, 7, 8}\big],$$

Besides these, let other sets be defined:

$$D = (A \cap \overline B) \cup (\overline A \cap B),$$

$$E = (A \cup B) \cap (\overline A \cup \overline B), $$

$$F = (A \cup C) \cap \overline B, $$

$$G = (\overline A \cap \overline C) \cup (A \cap B \cap C).$$

First consider which digits belong to the sets  $D$,  $E$,  $F$  and  $H$  and then answer the following questions.
Justify your answers in terms of set theory.

Hints:

• The task belongs to the chapter  Set theory basics.

• The topic of this chapter is illustrated with examples in the (German language) learning videoMengentheoretische Begriffe und Gesetzmäßigkeiten \Rightarrow.

Fragebogen

1

Welche der folgenden Aussagen sind richtig?

	$A$  und  $B$  sind disjunkte Mengen.
	$A$  und  $C$  sind disjunkte Mengen.
	$B$  und  $C$  sind disjunkte Mengen.

2

Welche der folgenden Aussagen sind richtig?

	Die Vereinigungsmenge  $A \cup B \cup C$  ergibt die Grundmenge  $G$.
	Die Komplementärmenge zu  $A \cap B \cap C$  ergibt die Grundmenge  $G$.

3

Welche der folgenden Aussagen sind richtig?

	Die Komplementärmengen von  $D$  und  $E$  sind identisch.
	$F$  ist eine Teilmenge der Komplementärmenge von  $B$.
	Die Mengen  $B$,  $C$  und  $D$  bilden ein vollständiges System.
	Die Mengen  $A$,  $C$  und  $H$  bilden ein vollständiges System.

Musterlösung

Solution

Für die weiteren in der Aufgabe definierten Mengen gilt:

$$ D = (A \cap \overline B) \cup (\overline A \cap B) =\big[\{1, 2, 3\} \cap \{1, 2, 4, 5, 7, 8\}\big] \cup \big[\{4, 5, 6, 7, 8, 9\} \cap \{3, 6, 9\}\big] = \{1, 2, 6, 9\},$$

$$ E = (A \cup B) \cap (\overline A \cup \overline B) = (A \cap \overline A) \cup (A \cap \overline B) \cup (\overline A \cap B) \cup (\overline A \cap \overline B) = (A \cap \overline B) \cup (\overline A \cap B) = D = \{1, 2, 6, 9\},$$

$$F = (A \cup C= \cap \overline B = \{1, 2, 3, 5, 6, 7, 8\} \cap \{1, 2, 4, 5, 7, 8\} = \{1, 2, 5, 7, 8\},$$

$$H = (\bar A \cap \overline C) \cup (A \cap B \cap C) = (\overline A \cap \overline C) \cup \phi = \{4, 9\}.$$

(1)  Richtig ist nur der Lösungsvorschlag 2:

• $A$  und  $C$  haben kein gemeinsames Element.
• $A$  und  $B$  beinhalten jeweils die  $3$.
• $B$  und  $C$  beinhalten jeweils die  $6$.

(2)  Richtig ist der Lösungsvorschlag 2:

• Keine Ziffer ist gleichzeitig in  $A$,  $B$  und  $C$  enthalten   ⇒   $ A \cap B \cap C = \phi$   ⇒   $ \overline{A \cap B \cap C} = \overline{\phi} = G$.
• Der erste Vorschlag ist dagegen falsch. Es fehlt die  $4$.

(3)  Richtig sind die Lösungsvorschläge 1, 2 und 4:

• Der erste Vorschlag ist richtig:   Die Mengen  $D$  und  $E$  enthalten genau die gleichen Elemente und somit auch deren Komplementärmengen.
• Auch der zweite Vorschlag ist richtig:   Allgemein, das heißt für beliebige  $X$  und  $B$  gilt:  $X \cap \overline B \subset \overline B \ \Rightarrow$   Mit $X = A \cup C$ folgt somit $F \subset \overline B$.
• Auch der letzte Vorschlag ist richtig:   $A = \{1, 2, 3\},$  $C = \{5, 6, 7, 8\}$  und  $H = \{4, 9\}$ bilden ein "vollständiges System".
• Der dritte Vorschlag ist dagegen falsch, weil  $B$  und  $C$  nicht disjunkt sind.