Aufgaben:Exercise 2.2: Modulation Depth

• Return to book

Modulationsgrad-Definition bei ZSB–AM

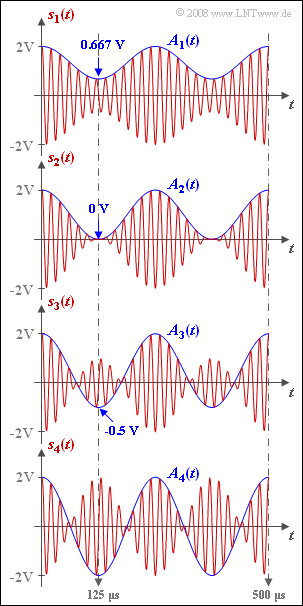
The graph shows DSB amplitude-modulated signals  $s_1(t)$  to  $s_4(t)$  with differing modulation depth  $m$. Let message signal  $q(t)$  and carrier signal  $z(t)$  each be cosine:

$$q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} f_{\rm N} = 4\,{\rm kHz}\hspace{0.05cm},$$

$$ z(t) = \hspace{0.2cm}1 \hspace{0.15cm} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} f_{\rm T} = 50\,{\rm kHz}\hspace{0.05cm}.$$

The modulated signal (transmitted signal) with the DC component added in the modulator is  $A_{\rm T}$:

$$s(t ) = A(t) \cdot z(t), \hspace{0.2cm} A(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$

In the graphs, the chosen normalization was:

$$A_{\rm T}+ A_{\rm N} = 2\,{\rm V}\hspace{0.05cm}.$$

• If the modulation depth is  $m ≤ 1$, then  $A(t)= q(t) + A_{\rm T}$  is equal to the envelope  $a(t)$.
• In contrast, for a modulation depth  $m > 1$:

$$a(t ) = |A(t)|\hspace{0.05cm}.$$

• The cosine curve  $A(t)$  varies between  $A_{\rm max}$  and  $A_{\rm min}$; because of normalization,  $A_{\rm max} = 2 \ \rm V$ is always the case.
• The minimum values of  $A(t)$  occur at half the period of the source signal $($i.e., for  $t = 125 \ \rm µ s)$ :

$$A_{\rm min} = q(T_0/2)+ A_{\rm T} = A_{\rm T}-A_{\rm N}.$$

• The numerical values are given in the graph.

Hints:

• This exercise belongs to the chapter   Double-Sideband Amplitude Modulation.
• Particular reference is made to the page  DSB-AM with carrier.

Questions

1

Determine the modulation depth for each of the signals  $s_1(t)$,  $s_2(t)$,  $s_3(t)$ .

$m_1 \ = \ $

$m_2 \ = \ $

$m_3 \ = \ $

2

Which statements are true for the signal  $s_4(t)$ ?

	This is a case of "DSB–AM without a carrier".
	The modulation depth is  $m = 0$.
	The modulation depth  $m$  is infinite.

3

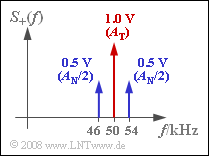
Let  $A_{\rm T} = A_{\rm N} = 1\ \rm V$, so  $m = 1$.  What is the spectrum  $S_+(f)$  of the analytical signal?
Which Dirac weights occur at  $f_{\rm T}$  as well as at  $f_{\rm T}± f_{\rm N}$ ?

$S_+(f_{\rm T}) \ = \ $ $\ \text{V}$

$S_+(f_{\rm T} ± f_{\rm N}) \ = \ $ $\ \text{V}$

4

Now let  $m = 1$.  Which fraction  $P_{\rm T}/P_{\rm S}$  of the total transmission power  $P_{\rm S}$  is due to the carrier alone, and thus cannot be used for demodulation??

$P_{\rm T}/P_{\rm S} \ = \ $

5

Generalize the result from   (4)  for an arbitrary modulation depth $m$.
What are the power ratios for  $m = 0.5$,  $m = 3$  and  $m → ∞$ ?

$m = 0.5\text{:}\hspace{0.3cm} P_{\rm T}/P_{\rm S} \ = \ $

$m = 3.0\text{:}\hspace{0.3cm} P_{\rm T}/P_{\rm S} \ = \ $

$m → ∞ \text{:}\hspace{0.3cm} P_{\rm T}/P_{\rm S} \ = \ $

6

Based on the calculations so far, which of the following assessments seem reasonable to you?

	$m ≈ 1$  s more favorable than a small  $m$ for energy reasons.
	The carrier is only useful for envelope demodulation.

Solution

Solution

(1)  From the two equations

$$ A_{\rm max} = A_{\rm T}+A_{\rm N}=2\,\,{\rm V},\hspace{0.3cm} A_{\rm min} = A_{\rm T}-A_{\rm N}\hspace{0.05cm}$$

directly follows:

$$A_{\rm N} = (A_{\rm max} - A_{\rm min})/2,\hspace{0.3cm} A_{\rm T} = (A_{\rm max} + A_{\rm min})/2\hspace{0.05cm}.$$

• Thus, the modulation depth is

$$m = \frac{A_{\rm max} - A_{\rm min}}{A_{\rm max} + A_{\rm min}}\hspace{0.05cm}.$$

• With the given numerical values, one obtains:

$$ m_1 = \frac{2\,{\rm V} - 0.667\,{\rm V}}{2\,{\rm V} + 0.667\,{\rm V}} \hspace{0.15cm}\underline {= 0.5}\hspace{0.05cm}, \hspace{0.5cm} m_2 = \frac{2\,{\rm V} - 0\,{\rm V}}{2\,{\rm V} + 0\,{\rm V}} \hspace{0.15cm}\underline {= 1.0}\hspace{0.05cm}, \hspace{0.5cm} m_3 = \frac{2\,{\rm V} -(-1\,{\rm V})}{2\,{\rm V} + (-1\,{\rm V})} \hspace{0.15cm}\underline{=3.0}\hspace{0.05cm}.$$

(2)  Answers 1 and 3 are correct:

• In diesem Fall ist  $A_{\rm T} = 0$, das heißt, es liegt tatsächlich eine  „ZSB–AM ohne Träger”  vor.
• Der Modulationsgrad  $m = A_{\rm N}/A_{\rm T}$  ist unendlich groß.

Spektrum: Analytisches Signal

(3)  Das Spektrum  $S_+(f)$  setzt sich für jeden Modulationsgrad  $m$  aus drei Diraclinien zusammen mit folgenden Gewichten:

• $A_{\rm T}$  $($bei  $f = f_{\rm T})$,
• $m/2 · A_{\rm T}$  $($bei  $f = f_{\rm T} ± f_{\rm N})$.

Für $m = 1$ ergeben sich die Gewichte entsprechend der Skizze:

• $S_+(f_{\rm T}) = 1\ \rm V$,
• $S_+(f_{\rm T} ± f_{\rm T}) = 0.5\ \rm V$.

(4)  Die auf den Widerstand  $1 \ Ω$  bezogene Leistung  (Quadrat des Effektivwertes)  einer harmonischen Schwingung mit der Amplitude  $A_{\rm T} = 1 \ \rm V$  beträgt:

$$P_{\rm T} ={A_{\rm T}^2}/{2} = 0.5\,{\rm V}^2 \hspace{0.05cm}.$$

• In gleicher Weise erhält man für die Leistungen des unteren und des oberen Seitenbandes:

$$P_{\rm USB} = P_{\rm OSB} =({A_{\rm N}}/{2})^2/2 = 0.125\,{\rm V}^2 \hspace{0.05cm}.$$

• Das gesuchte Verhältnis ist somit für  $m=1$:

$${P_{\rm T}}/{P_{\rm S}}= \frac{P_{\rm T}}{P_{\rm USB} + P_{\rm T}+ P_{\rm OSB}}= \frac{0.5\,{\rm V}^2}{0.125\,{\rm V}^2 + 0.5\,{\rm V}^2+ 0.125\,{\rm V}^2}= 2/3\hspace{0.15cm}\underline { = 0.667}\hspace{0.05cm}.$$

(5)  Mit den Diracgewichten  $m/2 · A_{\rm T}$  der beiden Seitenbänder entsprechend der Teilaufgabe  (3)  erhält man:

$${P_{\rm T}}/{P_{\rm S}}= \frac{A_{\rm T}^2/2}{A_{\rm T}^2/2 + 2 \cdot (m/2)^2 \cdot A_{\rm T}^2/2}= \frac{2}{2 + m^2}\hspace{0.05cm}.$$

• Dies führt zu den Zahlenwerten  $8/9 = 0.889$  $($für  $m = 0.5)$,     $2/11 = 0.182$  $($für  $m = 3)$  und     $0$  $($für  $m \to ∞$).

(6)  Beide Aussagen treffen zu:

• Die Zusetzung des Trägers macht nur Sinn, um den einfacheren Hüllkurvendemodulator verwenden zu können.  Dies geht nur für  $m \le 1$.
• Ist dagegen der Modulationsgrad  $m > 1$  und somit der Einsatz eines Synchrondemodulators erforderlich, sollte man aus energetischen Gründen auf den Träger (fast) ganz verzichten.
• Ebenso ist bei Anwendung eines Hüllkurvendemodulators aus energetischen Gründen ein möglichst großer Modulationsgrad  $m < 1$    ⇒   $m \to 1$  anzustreben.
• Allerdings kann durch einen kleinen Restträger die Trägerrückgewinnung erleichtert werden, die beim Synchrondemodulator zur Frequenz– und Phasensynchronisation benötigt wird.  Die zweite Aussage ist somit nur bedingt als richtig zu bewerten.