Difference between revisions of "Modulation Methods/Direct-Sequence Spread Spectrum Modulation"
| Line 30: | Line 30: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | This process is referred to as '''Direct Sequence Spread Spectrum''' $\rm (DS–SS)$ | + | This process is referred to as '''Direct Sequence Spread Spectrum''' $\rm (DS–SS)$ or PN band spreading. In this context, please note in particular: |
*In previous chapters, a major goal of modulation has always been to be as bandwidth-efficient as possible. | *In previous chapters, a major goal of modulation has always been to be as bandwidth-efficient as possible. | ||
*Here, in contrast, we try to spread the signal over as wide a bandwidth as possible. | *Here, in contrast, we try to spread the signal over as wide a bandwidth as possible. | ||
| Line 88: | Line 88: | ||
| − | + | After thresholding the samples $d(νT)$, one nevertheless obtains mostly the sought amplitude coefficients. The vague statement "mostly" is quantifiable by the bit error probability $p_{\rm B}$. Because of | |
:$$b(t) = \big [ s(t) + n(t) \big ] \cdot c(t) = q(t) + n(t) \cdot c(t)$$ | :$$b(t) = \big [ s(t) + n(t) \big ] \cdot c(t) = q(t) + n(t) \cdot c(t)$$ | ||
| − | + | and due to the fact that the statistical properties of white noise $n(t)$ are not changed by the multiplication with the $±1$ signal $c(t)$, the same result is obtained again as for the [[Modulation_Methods/Lineare_digitale_Modulation#Fehlerwahrscheinlichkeiten_-_ein_kurzer_.C3.9Cberblick|conventional BPSK]] without band spreading/band compression, independent of the spreading degree $J$ : | |
:$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B} }/{N_{\rm 0} } } \hspace{0.05cm} \right ) \hspace{0.05cm}.$$ }} | :$$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B} }/{N_{\rm 0} } } \hspace{0.05cm} \right ) \hspace{0.05cm}.$$ }} | ||
| − | == | + | ==Additional sinusoidal interferer around the carrier frequency== |
<br> | <br> | ||
| − | + | We continue to assume only one participant. In contrast to the calculation in the last section, however, there are now | |
| − | * | + | *in addition to the AWGN noise $n(t)$ also |
| − | * | + | *a narrowband interferer $i(t)$ around the frequency $f_{\rm I}$ with power $P_{\rm I}$ and bandwidth $B_{\rm I}$. |
| − | + | In the limiting case $B_{\rm I} → 0$ the power density spectrum of this "sinusoidal interferer" is: | |
:$${\it \Phi}_{\rm I}(f) = {P_{\rm I}}/{2} \cdot \big[ \delta ( f - f_{\rm I}) + \delta ( f + f_{\rm I}) \big ] \hspace{0.05cm}.$$ | :$${\it \Phi}_{\rm I}(f) = {P_{\rm I}}/{2} \cdot \big[ \delta ( f - f_{\rm I}) + \delta ( f + f_{\rm I}) \big ] \hspace{0.05cm}.$$ | ||
| − | + | In a conventional transmission system without band spreading/band compression, such a narrowband interferer would increase the error probability to an unacceptable extent. In a system with band spreading ⇒ direct-sequence spread spectrum modulation, the interfering influence is significantly lower, since | |
| − | * | + | *band compression acts as band spreading at the receiver with respect to the sinusoidal interferer, |
| − | * | + | * thus its power is distributed over a very wide frequency band $B_c = 1/T_c \gg B$, |
| − | * | + | *the additional interfering power density in the useful frequency band $(±B)$ is rather low and can be detected by a slight increase of the AWGN noise power density $N_0$. |
| − | + | With $T = J · T_c$ and $B = 1/T$ one obtains: | |
| − | :$$p_{\rm B} \approx {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0} +P_{\rm I} \cdot T_c} } \hspace{0.05cm} \right ) = {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0} } \cdot \left( \frac{1}{1+ P_{\rm I} \cdot T_c/N_0}\right ) } \hspace{0.05cm} \right )\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{ | + | :$$p_{\rm B} \approx {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0} +P_{\rm I} \cdot T_c} } \hspace{0.05cm} \right ) = {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0} } \cdot \left( \frac{1}{1+ P_{\rm I} \cdot T_c/N_0}\right ) } \hspace{0.05cm} \right )\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{SNR degradation:} \ \frac{1}{\big[1 + P_{\rm I}/(J · N_0 · B)\big]}\hspace{0.05cm}.$$ |
| − | + | The larger the spreading factor $J$, the smaller the increase in noise power due to the sinusoidal interferer. | |
| − | '' | + | ''Note:'' This fact has led to the spreading factor $J$ being often referred to as spreading gain in the literature, compare for example [ZP85]<ref>Ziemer, R.; Peterson, R. L.: ''Digital Communication and Spread Spectrum Systems.'' New York: McMillon, 1985.</ref>. |
| − | * | + | *These books are mostly about military applications of the band spreading methods. |
| − | * | + | *Sometimes the "cheapest interferer" is mentioned, namely when the degradation is the largest. |
| − | * | + | *However, we do not want to deal with such applications here. |
| − | + | Approximately, however, the above error probability equation can also be applied when an unspread transmission of higher data rate and a spread spectrum system of lower rate operate in the same frequency band. The interfering influence of the former system with bandwidth $B_{\rm I}$ on the spread spectrum system can be treated approximately as a ''narrowband interferer'' as long as $B_{\rm I}$ is sufficiently small. | |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{ | + | $\text{Conclusion:}$ |
| − | * | + | *With AWGN noise (and also many other channels), the bit error probability cannot be reduced by band spreading. |
| − | * | + | *In the best case, band spreading results in the same bit error probability as BPSK (without spreading). |
| − | * | + | *For our purposes, band spreading is a necessary measure to be able to supply several subscribers simultaneously in the same frequency band. |
| − | * | + | *In the following, we will only consider the CDMA aspect and therefore continue to speak of the spreading factor $J$ and not of a spreading gain. }} |
==Exercises for the chapter== | ==Exercises for the chapter== | ||
<br> | <br> | ||
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_5.2:_Bandspreading_and_Narrowband_Interferer|Exercise 5.2: Bandspreading and Narrowband Interferer]] |
| − | [[Aufgaben: | + | [[Aufgaben:Exercise_5.2Z:_About_PN_Modulation|Exercise 5.2Z: About PN Modulation]] |
Revision as of 13:33, 29 November 2021
Contents
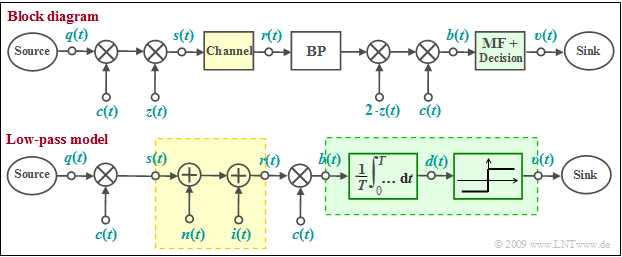
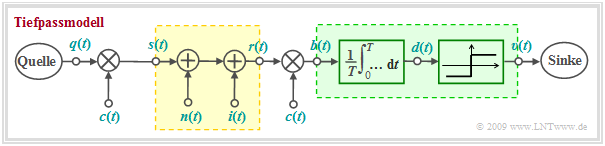
Block diagram and equivalent low-pass model
One possibility for realizing a CDMA system is the so-called direct-sequence spread spectrum, which is explained here on the basis of the block diagram. The corresponding model in the equivalent low-pass range is shown below.
In both models, the distortion-free channel $($AWGN and possibly interference from other users, but no intersymbol interference$)$ is highlighted in yellow and the optimal receiver $($matched filter plus threshold decider$)$ is highlighted in green.
$\text{This system can be characterized as follows:}$
- If the multiplication with the spread signal $c(t)$ at transmitter and receiver is omitted, the result is a conventional BPSK system with the carrier $z(t)$ and AWGN noise, characterized by the additive Gaussian interference signal $n(t)$. The second interference component (interference from other participants) is omitted: $i(t) = 0$.
- For the following it is assumed $($this is essential for direct-sequence spread spectrum!$)$ that the source signal $q(t)$ has a rectangular NRZ curve. Then the matched filter can be replaced by an integrator over a symbol duration $T$ ⇒ "Integrate & Dump". This is followed by the threshold decider.
Principle and properties of band spreading methods
In the following we consider direct-sequence spread spectrum in the equivalent low-pass range. Thus, the multiplication with the carrier signals $z(t)$ or $2\cdot z(t)$ is omitted.
- Characteristic for this type of modulation is the multiplication of the bipolar and rectangular digital signal $q(t)$ with a pseudo-random $±1$ spreading sequence $c(t)$:
- $$s(t) = q(t) \cdot c(t) \hspace{0.05cm}.$$
- The duration $T_c$ of a spreading chip is smaller than the duration $T$ of a source symbol by the integer spreading factor $J$, so that the transmitted signal spectrum is
- $$S(f) = Q(f) \star C(f)$$
- is wider than the spectral function $Q(f)$ by approximately this factor $J$ .
This process is referred to as Direct Sequence Spread Spectrum $\rm (DS–SS)$ or PN band spreading. In this context, please note in particular:
- In previous chapters, a major goal of modulation has always been to be as bandwidth-efficient as possible.
- Here, in contrast, we try to spread the signal over as wide a bandwidth as possible.
- The bandwidth expansion by $J$ is necessary to allow several subscribers to use the same frequency band simultaneously.
- Ideally, $2^J$ suitable spreading sequences can be found. This makes a CDMA system for $2^J$ simultaneous users feasible.
Band spreading techniques also offer the following advantages:
- One can transmit an additional low-rate "DS–SS signal" can be transmitted over a frequency band that is otherwise used by FDMA channels with a higher data rate without significantly disrupting the main applications. The band spread signal virtually disappears under the noise level of these signals.
- Targeted narrowband interferers ("sinusoidal interferers") can be combated well with this technique. This military point of view was also decisive for the invention and further development of band spreading techniques.
- Furthermore, the band spreading technique in general, but especially frequency hopping $($fast discrete change of the carrier frequency over a wide range$)$ and chirp modulation $($continuous change of the carrier frequency during a bit interval$)$ also offer the possibility of better transmission over frequency-selective channels.
Signal curves with a single participant
A disadvantage of direct-sequence spread spectrum modulation is that under unfavorable conditions interference can occur between the subscriber under consideration and other subscribers.
- This case is taken into account in the model by the interference quantity $i(t)$.
- We initially consider only one transmitter, so that $i(t) = 0$ is to be set.
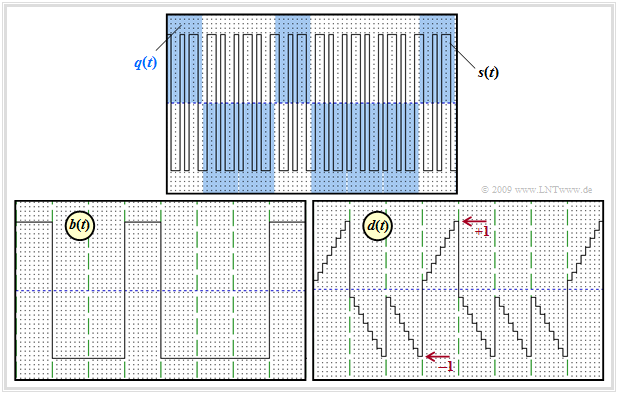
$\text{Example 1:}$
The graph shows
- above the source signal $q(t)$ – marked by the blue background – and the (band spread) transmitted signal $s(t)$,
- at the bottom left the signal $b(t)$ after band compression, and
- bottom right the detection signal $d(t)$ after the integrator, directly before the decision maker.
Further notes:
- A discrete-time and normalized signal representation with rectangles spaced by the chip duration $T_c$ is chosen.
- The spreading factor is $J = 8$.
- As spreading sequence the walsh function no. 7 is used.
- All images are valid for the noise-free case ⇒ $n(t) = 0$.
To the individual signal curves is to be noted:
- The $±1$ data signal $q(t)$ is marked by the blue background. After multiplication with the spread signal $c(t)$, the result is the transmitted signal $J = 8$ which is higher in frequency by the factor $s(t)$.
- The spread signal $c(t)$ is periodic with $T = J · T_c$ and thus has a line spectrum. In the first, fourth, and eighth data bits, $c(t)=s(t)$, but at the other times, $c(t) = - s(t)$.
- After band compression at the receiver, i.e., after chipsynchronous multiplication by $c(t) ∈ \{±1\}$ ⇒ $c^2(t) = 1$ , the signal $b(t)$ is obtained.
- In the distortion-free and noise-free case
- $$b(t) = r(t) \cdot c(t) = s(t) \cdot c(t) = \big [ q(t) \cdot c(t) \big ] \cdot c(t) = q(t) \hspace{0.05cm}.$$
- Integrating $b(t)$ over one bit at a time yields a linearly increasing or linearly decreasing signal $d(t)$. The step curve in the right image is solely due to the discrete-time representation.
- At the equidistant detection times the $ν$–th amplitude coefficients $a_ν$ of the source signal $q(t)$ are valid in the distortion- and noise-free case:
- $$ d (\nu T) = \frac{1}{T} \cdot \hspace{-0.1cm} \int_{(\nu -1 )T }^{\nu T}\hspace{-0.3cm} b (t )\hspace{0.1cm} {\rm d}t = a_\nu \in \{ +1, -1 \}\hspace{0.05cm}.$$
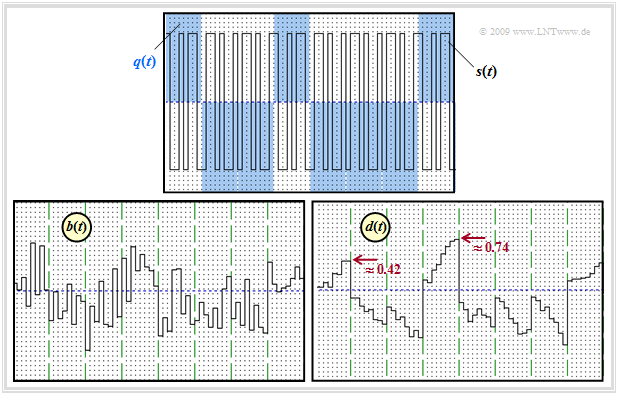
$\text{Example 2:}$
The two lower graphs change significantly from the first example when AWGN noise is considered.
The AWGN parameter is assumed to be $10 · \lg \ (E_{\rm B}/N_0) = 6 \ \rm dB$. Then
- das bandpassed signal $b(t)$ is no longer sectionally constant, and
- the detection signal $d(t)$ is no longer linearly increasing or decreasing.
After thresholding the samples $d(νT)$, one nevertheless obtains mostly the sought amplitude coefficients. The vague statement "mostly" is quantifiable by the bit error probability $p_{\rm B}$. Because of
- $$b(t) = \big [ s(t) + n(t) \big ] \cdot c(t) = q(t) + n(t) \cdot c(t)$$
and due to the fact that the statistical properties of white noise $n(t)$ are not changed by the multiplication with the $±1$ signal $c(t)$, the same result is obtained again as for the conventional BPSK without band spreading/band compression, independent of the spreading degree $J$ :
- $$p_{\rm B} = {\rm Q} \left( \hspace{-0.05cm} \sqrt { {2 \cdot E_{\rm B} }/{N_{\rm 0} } } \hspace{0.05cm} \right ) \hspace{0.05cm}.$$
Additional sinusoidal interferer around the carrier frequency
We continue to assume only one participant. In contrast to the calculation in the last section, however, there are now
- in addition to the AWGN noise $n(t)$ also
- a narrowband interferer $i(t)$ around the frequency $f_{\rm I}$ with power $P_{\rm I}$ and bandwidth $B_{\rm I}$.
In the limiting case $B_{\rm I} → 0$ the power density spectrum of this "sinusoidal interferer" is:
- $${\it \Phi}_{\rm I}(f) = {P_{\rm I}}/{2} \cdot \big[ \delta ( f - f_{\rm I}) + \delta ( f + f_{\rm I}) \big ] \hspace{0.05cm}.$$
In a conventional transmission system without band spreading/band compression, such a narrowband interferer would increase the error probability to an unacceptable extent. In a system with band spreading ⇒ direct-sequence spread spectrum modulation, the interfering influence is significantly lower, since
- band compression acts as band spreading at the receiver with respect to the sinusoidal interferer,
- thus its power is distributed over a very wide frequency band $B_c = 1/T_c \gg B$,
- the additional interfering power density in the useful frequency band $(±B)$ is rather low and can be detected by a slight increase of the AWGN noise power density $N_0$.
With $T = J · T_c$ and $B = 1/T$ one obtains:
- $$p_{\rm B} \approx {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0} +P_{\rm I} \cdot T_c} } \hspace{0.05cm} \right ) = {\rm Q} \left( \hspace{-0.05cm} \sqrt { \frac{2 \cdot E_{\rm B}}{N_{\rm 0} } \cdot \left( \frac{1}{1+ P_{\rm I} \cdot T_c/N_0}\right ) } \hspace{0.05cm} \right )\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\text{SNR degradation:} \ \frac{1}{\big[1 + P_{\rm I}/(J · N_0 · B)\big]}\hspace{0.05cm}.$$
The larger the spreading factor $J$, the smaller the increase in noise power due to the sinusoidal interferer.
Note: This fact has led to the spreading factor $J$ being often referred to as spreading gain in the literature, compare for example [ZP85][1].
- These books are mostly about military applications of the band spreading methods.
- Sometimes the "cheapest interferer" is mentioned, namely when the degradation is the largest.
- However, we do not want to deal with such applications here.
Approximately, however, the above error probability equation can also be applied when an unspread transmission of higher data rate and a spread spectrum system of lower rate operate in the same frequency band. The interfering influence of the former system with bandwidth $B_{\rm I}$ on the spread spectrum system can be treated approximately as a narrowband interferer as long as $B_{\rm I}$ is sufficiently small.
$\text{Conclusion:}$
- With AWGN noise (and also many other channels), the bit error probability cannot be reduced by band spreading.
- In the best case, band spreading results in the same bit error probability as BPSK (without spreading).
- For our purposes, band spreading is a necessary measure to be able to supply several subscribers simultaneously in the same frequency band.
- In the following, we will only consider the CDMA aspect and therefore continue to speak of the spreading factor $J$ and not of a spreading gain.
Exercises for the chapter
Exercise 5.2: Bandspreading and Narrowband Interferer
Exercise 5.2Z: About PN Modulation
References
- ↑ Ziemer, R.; Peterson, R. L.: Digital Communication and Spread Spectrum Systems. New York: McMillon, 1985.