Difference between revisions of "Aufgaben:Exercise 1.7Z: BARBARA Generator"
From LNTwww
| Line 2: | Line 2: | ||
{{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Markov_Chains}} | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Markov_Chains}} | ||
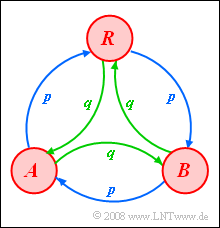
| − | [[File:P_ID454__Sto_Z_1_7.png|right|frame|$BARBARA$ Generator]] | + | [[File:P_ID454__Sto_Z_1_7.png|right|frame|$\rm BARBARA$ Generator]] |
| − | Here we consider a ternary random generator with symbols $A$, $B$ and $R$, which can be described by a homogeneous and stationary first order Markov chain. | + | Here we consider a ternary random generator with symbols $A$, $B$ and $R$, which can be described by a homogeneous and stationary first order Markov chain. |
*The transition probabilities can be taken from the sketched Markov diagram. | *The transition probabilities can be taken from the sketched Markov diagram. | ||
| Line 14: | Line 14: | ||
Hints: | Hints: | ||
| − | *The | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Markov_Chains|Markov Chains]]. |
| Line 24: | Line 24: | ||
|type="[]"} | |type="[]"} | ||
- The values of $p > 0$ and $q < 1$ are largely arbitrary. | - The values of $p > 0$ and $q < 1$ are largely arbitrary. | ||
| − | + For the transition probabilities, the following must hold: $p + q = 1$. | + | + For the transition probabilities, the following must hold: $p + q = 1$. |
+ All symbols have equal ergodic probabilities. | + All symbols have equal ergodic probabilities. | ||
- It holds here: ${\rm Pr}(A) = 1/2, \; {\rm Pr}(B) = 1/3, \; {\rm Pr}(R) = 1/6$. | - It holds here: ${\rm Pr}(A) = 1/2, \; {\rm Pr}(B) = 1/3, \; {\rm Pr}(R) = 1/6$. | ||
| − | {What are the conditional probabilities $p_{\rm A}$, $p_{\rm B}$ and $p_{\rm C}$ that at times between $ν+1$ and $ν+7$ the sequence $BARBARA$ is output, <br>if one is in state | + | {What are the conditional probabilities $p_{\rm A}$, $p_{\rm B}$ and $p_{\rm C}$ that at times between $ν+1$ and $ν+7$ the sequence "$\rm BARBARA$" is output, <br>if one is at time $ν$ in state $A$, $B$ or $R$, respectively? Let $p = 1/4$. |
|type="{}"} | |type="{}"} | ||
$p_{\rm A} \ = \ $ { 0.549 3% } $\ \cdot 10^{-3}$ | $p_{\rm A} \ = \ $ { 0.549 3% } $\ \cdot 10^{-3}$ | ||
| Line 34: | Line 34: | ||
$p_{\rm C} \ = \ $ { 0.183 3% } $\ \cdot 10^{-3}$ | $p_{\rm C} \ = \ $ { 0.183 3% } $\ \cdot 10^{-3}$ | ||
| − | {What is the overall probability that the generator outputs the sequence $BARBARA$ | + | {What is the overall probability that the generator outputs the sequence "$\rm BARBARA$"? Let $p = 1/4$ continue to hold. |
|type="{}"} | |type="{}"} | ||
| − | ${\rm Pr}(BARBARA)\ = \ $ { 0.244 3% } $\ \cdot 10^{-3}$ | + | ${\rm Pr}(\rm BARBARA)\ = \ $ { 0.244 3% } $\ \cdot 10^{-3}$ |
| − | {How should the parameter $p_{\rm opt}$ be chosen to make ${\rm Pr}(BARBARA)$ as large as possible? <br>What is the resulting probability for $BARBARA$? | + | {How should the parameter $p_{\rm opt}$ be chosen to make ${\rm Pr}(\rm BARBARA)$ as large as possible? <br>What is the resulting probability for "$\rm BARBARA$"? |
|type="{}"} | |type="{}"} | ||
$p_{\rm opt} \ = \ $ { 0.8333 3% } | $p_{\rm opt} \ = \ $ { 0.8333 3% } | ||
| − | $p = p_{\rm opt}\hspace{-0.1cm}: \hspace{0.3cm}{\rm Pr}(BARBARA)\ = \ $ { 22 3% } $\ \cdot 10^{-3}$ | + | $p = p_{\rm opt}\hspace{-0.1cm}: \hspace{0.3cm}{\rm Pr}(\rm BARBARA)\ = \ $ { 22 3% } $\ \cdot 10^{-3}$ |
</quiz> | </quiz> | ||
Revision as of 14:44, 2 December 2021
Here we consider a ternary random generator with symbols $A$, $B$ and $R$, which can be described by a homogeneous and stationary first order Markov chain.
- The transition probabilities can be taken from the sketched Markov diagram.
- For the first three subtasks, $p = 1/4$ should always hold.
Hints:
- The exercise belongs to the chapter Markov Chains.
Questions
Musterlösung
(1) Correct are the second and third suggested solutions:
- The sum of all outgoing arrows must always be $1$ . Therefore $q = 1 - p$ holds.
- Because of the symmetry of the Markov diagram, the ergodic probabilities are all equal:
- $${\rm Pr}(A) ={\rm Pr}(B) ={\rm Pr}(R) = 1/3.$$
(2) If one is in the state $B$ at the starting time $\nu=1$ because of ${\rm Pr}(B\hspace{0.05cm}|\hspace{0.05cm}B) = 0$ the state $B$ is not possible.
- One fails here already with the initial letter $B$:
- $$p_{\rm B} \; \underline{ =0}.$$
- For the calculation of $p_{\rm A}$ it should be noted: Starting from $A$ one goes in the Markov diagram first to $B$ $($with probability $q)$, then five times clockwise $($each time with probability $p)$ and finally from $R$ to $A$ $($with probability $q)$. Meaning:
- $$p_{\rm A} = q^2 \hspace{0.05cm}\cdot \hspace{0.05cm} p^5 = 3^2 / 4^7 \hspace{0.15cm}\underline {\approx 0.549 \hspace{0.05cm}\cdot \hspace{0.05cm} 10^{-3}}.$$
- In a similar way, one obtains:
- $$p_{\rm R} = q \hspace{0.05cm}\cdot \hspace{0.05cm} p^6 = 3 / 4^7 \hspace{0.15cm}\underline {\approx 0.183 \hspace{0.05cm}\cdot \hspace{0.05cm} 10^{-3}}.$$
(3) By averaging over the conditional probabilities we obtain:
- $${\rm Pr}(BARBARA) = p_{\rm A} \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm Pr}(A) \hspace{0.1cm} + \hspace{0.1cm}p_{\rm B} \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm Pr}(B) \hspace{0.1cm} + \hspace{0.1cm}p_{\rm R} \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm Pr}(R).$$
- This leads to the result:
- $${\rm Pr}(BARBARA) = {1}/{3} \cdot \left( q^2 \hspace{0.05cm}\cdot \hspace{0.05cm} p^5 \hspace{0.1cm} +\hspace{0.1cm}0 \hspace{0.1cm} +\hspace{0.1cm}q \hspace{0.05cm}\cdot \hspace{0.05cm} p^6 \right) = \frac{q \hspace{0.05cm}\cdot \hspace{0.05cm} p^5 }{3} \cdot{p+q} = \hspace{-0.15cm} \frac{q \hspace{0.05cm}\cdot \hspace{0.05cm} p^5 }{3} \hspace{0.15cm}\underline { \approx 0.244 \hspace{0.05cm}\cdot \hspace{0.05cm} 10^{-3}}.$$
(4) The probability calculated in (3) is $p^5 \cdot (1-p)/3$, where $q= 1-p$ is considered.
- By setting the differential to zero, we obtain the governing equation:
- $$5 \cdot p^4 - 6 \cdot p^5 = 0 \hspace{0.5cm} \Rightarrow \hspace{0.5cm} p_{\rm opt} = 5/6 \hspace{0.15cm}\underline { \approx \rm 0.833}.$$
- This results in a value that is larger than the subtask (3) by a factor $90$ approximately:
- $${\rm Pr}(BARBARA) \hspace{0.15cm}\underline { \approx 22 \hspace{0.05cm}\cdot \hspace{0.05cm} 10^{-3}}.$$