Difference between revisions of "Aufgaben:Exercise 5.3: PACF of PN Sequences"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1884__Mod_A_5_3.png|right|frame| | + | [[File:P_ID1884__Mod_A_5_3.png|right|frame|M–sequence $(P = 15)$ plus cyclic permutations]] |
| − | + | With a feedback shift register of degree $G$ a spreading sequence $〈c_ν〉$ with the (maximum) period length $P = 2^G - 1$ can be generated if the feedback coefficients (taps) are chosen correctly. | |
| − | In | + | In this exercise, we consider the PN generator with octal identifier $(31)$ shown in the left graph of [[Modulation_Methods/Spreizfolgen_für_CDMA#Pseudo.E2.80.93Noise.E2.80.93Folgen_maximaler_L.C3.A4nge|$\text{example 1}$]] in the theory section, which yields a sequence with period length $P = 15$ because of $G = 4$. |
| − | + | The graph for this exercise shows the unipolar sequence $〈u_ν〉$ with $u_ν ∈ \{0, 1\}$ and cyclic shifts $〈u_{ν+λ}〉$ derived from it, where the shift parameter $λ$ takes values between $1$ and $15$. Here, a shift by $λ$ means absolutely an offset by $λ · T_c$. Here, $T_c$ denotes the chip duration. | |
| − | + | For use in a CDMA system, however, one uses the bipolar (antipodal) sequence $〈c_ν〉$ with $c_ν ∈ \{+1, -1\}$, which is to be investigated starting in subtask '''(5)'''. We are looking for its periodic auto-correlation function (PACF) | |
:$${\it \varphi}_{c}(\lambda) = {\rm E} \big [ c_\nu \cdot c_{\nu+\lambda} \big ] \hspace{0.05cm}.$$ | :$${\it \varphi}_{c}(\lambda) = {\rm E} \big [ c_\nu \cdot c_{\nu+\lambda} \big ] \hspace{0.05cm}.$$ | ||
| − | + | In order to derive it, first the PACF | |
:$${\it \varphi}_{u}(\lambda) = {\rm E}\big [ u_\nu \cdot u_{\nu+\lambda} \big ]$$ | :$${\it \varphi}_{u}(\lambda) = {\rm E}\big [ u_\nu \cdot u_{\nu+\lambda} \big ]$$ | ||
| − | + | with the unipolar coefficients $u_ν ∈ \{0, 1\}$, will be calculated. The conversion of the coefficients is given by $c_ν = 1 - 2u_ν$. | |
| Line 21: | Line 21: | ||
| − | + | ''Note:'' | |
| − | '' | + | *The exercise belongs to the chapter [[Modulation_Methods/Spreizfolgen_für_CDMA|Spreading Sequences for CDMA]]. |
| − | * | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What is the degree of the PN generator? |
|type="{}"} | |type="{}"} | ||
$G \ = \ $ { 4 } | $G \ = \ $ { 4 } | ||
| − | { | + | {What is the expected squared value of the coefficients $u_ν ∈ \{0,\ 1\}$? |
|type="{}"} | |type="{}"} | ||
${\rm E}\big[u_ν^{\hspace{0.04cm}2}\big] \ = \ $ { 0.533 3% } | ${\rm E}\big[u_ν^{\hspace{0.04cm}2}\big] \ = \ $ { 0.533 3% } | ||
| − | { | + | {What is the expected squared value of the coefficients $c_ν ∈ \{+1, –1\}$? |
|type="{}"} | |type="{}"} | ||
${\rm E}\big[c_ν^{\hspace{0.04cm}2}\big] \ = \ $ { 1 3% } | ${\rm E}\big[c_ν^{\hspace{0.04cm}2}\big] \ = \ $ { 1 3% } | ||
| − | { | + | {Which statements are true for the expected value ${\rm E}\big[u_ν · u_{ν+λ}\big]$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + ${\rm E}\big[u_ν · u_{ν+1}\big] = 4/15$ is valid. |
| − | + | + | + ${\rm E}\big[u_ν · u_{ν+2}\big] = 4/15$ is valid. |
| − | - | + | - ${\rm E}\big[u_ν · u_{ν+15}\big] = 4/15$ is valid. |
| − | + | + | + The PACF values $φ_u(λ = 1)$, ... , $φ_u(λ = 14)$ are all equal. |
| − | { | + | {Calculate the PACF values with bipolar representation $(λ = 1, \text{...} \ , 14)$: |
|type="{}"} | |type="{}"} | ||
$φ_c(λ) \ = \ $ { -0.069--0.065 } | $φ_c(λ) \ = \ $ { -0.069--0.065 } | ||
| − | { | + | {Specify the following PACF values for the case $G = 6$. |
|type="{}"} | |type="{}"} | ||
$φ_c(λ=0)\hspace{0.33cm} = \ $ { 1 3% } | $φ_c(λ=0)\hspace{0.33cm} = \ $ { 1 3% } | ||
| Line 63: | Line 62: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The period of an M-sequence is $P = 2^G -1 \hspace{0.05cm}.$ This results with $P = 15$ the degree $\underline{G = 4}$. |
| − | '''(2)''' | + | '''(2)''' Of the $P = 15$ spreading bits, $8$ are ones and $7$ are zeros. Thus, because $u_ν^{\hspace{0.04cm}2} = u_ν$: |
:$${\rm E}\big [ u_\nu \big ] = {\rm E}\big [ u_\nu^2 \big ] = {8}/{15} \hspace{0.15cm}\underline {\approx 0.533} \hspace{0.05cm}, \hspace{0.3cm} \text{allgemein:}\,\, (P+1)/(2P)\hspace{0.05cm}.$$ | :$${\rm E}\big [ u_\nu \big ] = {\rm E}\big [ u_\nu^2 \big ] = {8}/{15} \hspace{0.15cm}\underline {\approx 0.533} \hspace{0.05cm}, \hspace{0.3cm} \text{allgemein:}\,\, (P+1)/(2P)\hspace{0.05cm}.$$ | ||
| − | '''(3)''' In | + | '''(3)''' In bipolar representation, it is always $c_ν^{\hspace{0.04cm}2} = 1$. Thus, also for the quadratic expectation value: |
:$${\rm E}\big [ c_\nu^{\hspace{0.04cm}2} \big ] \hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$ | :$${\rm E}\big [ c_\nu^{\hspace{0.04cm}2} \big ] \hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' <u>Solutions 1, 2 and 4</u> are correct: |
| − | * | + | *The attached table makes clear that for the discrete PACF values with $λ = 1$, ... , $14$ holds: |
:$${\it \varphi}_{u}(\lambda) = {\rm E}\big [ u_\nu \cdot u_{\nu+\lambda} \big ]= {4}/{15} \hspace{0.05cm}.$$ | :$${\it \varphi}_{u}(\lambda) = {\rm E}\big [ u_\nu \cdot u_{\nu+\lambda} \big ]= {4}/{15} \hspace{0.05cm}.$$ | ||
| − | * | + | *If we multiply 〈$u_ν$ 〉 with 〈$u_{ν+λ}$, where for the index $λ$ again the values $1$, ... , $14$ are to be used, then four ones occur in the product in each case. |
| − | * | + | *In contrast, for $λ = P = 15$: |
:$${\it \varphi}_{u}(\lambda = 15) = {\rm E}\big [ u_\nu \cdot u_{\nu+P} \big ]= {8}/{15} \hspace{0.05cm}.$$ | :$${\it \varphi}_{u}(\lambda = 15) = {\rm E}\big [ u_\nu \cdot u_{\nu+P} \big ]= {8}/{15} \hspace{0.05cm}.$$ | ||
| − | '''(5)''' | + | '''(5)''' The bipolar coefficients $c_ν$ result from the unipolar coefficients $u_ν$ according to the equation |
:$$c_\nu = 1 - 2 \cdot u_\nu \hspace{0.3cm} \Rightarrow \hspace{0.3cm} u_\nu = 0\text{:} \ \ c_\nu = +1\hspace{0.05cm},\hspace{0.3cm}u_\nu = 1\text{:} \ \ c_\nu = -1 \hspace{0.05cm}.$$ | :$$c_\nu = 1 - 2 \cdot u_\nu \hspace{0.3cm} \Rightarrow \hspace{0.3cm} u_\nu = 0\text{:} \ \ c_\nu = +1\hspace{0.05cm},\hspace{0.3cm}u_\nu = 1\text{:} \ \ c_\nu = -1 \hspace{0.05cm}.$$ | ||
| − | * | + | *Thus, it follows from the calculation rules for expected values: |
:$${\it \varphi}_{c}(\lambda) = {\rm E} \big [ c_\nu \cdot c_{\nu+\lambda} \big ]= {\rm E} \big [ (1 - 2 \cdot u_\nu ) \cdot (1 - 2 \cdot u_{\nu+\lambda} ) \big ] = 1 + 4 \cdot {\rm E}\big [ u_\nu \cdot u_{\nu+\lambda} \big ] - 2 \cdot {\rm E}\big [ u_\nu \big ] - 2 \cdot {\rm E}\big [ u_{\nu+\lambda} \big ] \hspace{0.05cm}.$$ | :$${\it \varphi}_{c}(\lambda) = {\rm E} \big [ c_\nu \cdot c_{\nu+\lambda} \big ]= {\rm E} \big [ (1 - 2 \cdot u_\nu ) \cdot (1 - 2 \cdot u_{\nu+\lambda} ) \big ] = 1 + 4 \cdot {\rm E}\big [ u_\nu \cdot u_{\nu+\lambda} \big ] - 2 \cdot {\rm E}\big [ u_\nu \big ] - 2 \cdot {\rm E}\big [ u_{\nu+\lambda} \big ] \hspace{0.05cm}.$$ | ||
| − | * | + | *Using the result of subtask '''(2)''' |
:$$ {\rm E}\left [ u_{\nu} \right ]= {\rm E}\left [ u_{\nu+\lambda} \right ]={8}/{15} \hspace{0.05cm},$$ | :$$ {\rm E}\left [ u_{\nu} \right ]= {\rm E}\left [ u_{\nu+\lambda} \right ]={8}/{15} \hspace{0.05cm},$$ | ||
| − | + | and the subtask '''(4)''' | |
:$${\rm E}\big [ u_\nu \cdot u_{\nu+\lambda} \big ] ={4}/{15} \hspace{0.05cm} \,\,{\rm{f\ddot{u}r}}\,\,\lambda = 0, \pm P, \pm 2P, \text{...}$$ | :$${\rm E}\big [ u_\nu \cdot u_{\nu+\lambda} \big ] ={4}/{15} \hspace{0.05cm} \,\,{\rm{f\ddot{u}r}}\,\,\lambda = 0, \pm P, \pm 2P, \text{...}$$ | ||
| − | + | one thus arrives at the result $($if $λ$ is not a multiple of $P)$: | |
:$${\it \varphi}_{c}(\lambda) = 1 + 4 \cdot \frac{4}{15} - 2 \cdot \frac{8}{15}- 2 \cdot \frac{8}{15} = - \frac{1}{15} = - \frac{1}{P}\hspace{0.15cm}\underline {\approx - 0.067} \hspace{0.05cm}.$$ | :$${\it \varphi}_{c}(\lambda) = 1 + 4 \cdot \frac{4}{15} - 2 \cdot \frac{8}{15}- 2 \cdot \frac{8}{15} = - \frac{1}{15} = - \frac{1}{P}\hspace{0.15cm}\underline {\approx - 0.067} \hspace{0.05cm}.$$ | ||
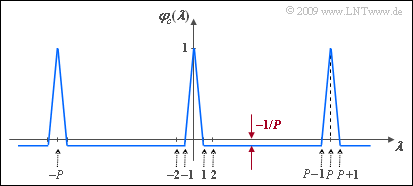
| − | [[File:P_ID1885__Mod_A_5_3f.png|right|frame| | + | [[File:P_ID1885__Mod_A_5_3f.png|right|frame|PACF of a PN sequence of maximum length]] |
| − | '''(6)''' | + | '''(6)''' A M-sequence with degree $G = 6$ has the period length $P = 63$. |
| − | * | + | *Corresponding to the result for subtask '''(5)''', we thus obtain: |
:$$ {\it \varphi}_{c}(\lambda = 0) \hspace{0.15cm}\underline {= +1} \hspace{0.05cm},$$ | :$$ {\it \varphi}_{c}(\lambda = 0) \hspace{0.15cm}\underline {= +1} \hspace{0.05cm},$$ | ||
:$$ {\it \varphi}_{c}(\lambda = 1)= - 1/63 \hspace{0.15cm}\underline {\approx - 0.016} \hspace{0.05cm},$$ | :$$ {\it \varphi}_{c}(\lambda = 1)= - 1/63 \hspace{0.15cm}\underline {\approx - 0.016} \hspace{0.05cm},$$ | ||
Revision as of 14:01, 10 December 2021
With a feedback shift register of degree $G$ a spreading sequence $〈c_ν〉$ with the (maximum) period length $P = 2^G - 1$ can be generated if the feedback coefficients (taps) are chosen correctly.
In this exercise, we consider the PN generator with octal identifier $(31)$ shown in the left graph of $\text{example 1}$ in the theory section, which yields a sequence with period length $P = 15$ because of $G = 4$.
The graph for this exercise shows the unipolar sequence $〈u_ν〉$ with $u_ν ∈ \{0, 1\}$ and cyclic shifts $〈u_{ν+λ}〉$ derived from it, where the shift parameter $λ$ takes values between $1$ and $15$. Here, a shift by $λ$ means absolutely an offset by $λ · T_c$. Here, $T_c$ denotes the chip duration.
For use in a CDMA system, however, one uses the bipolar (antipodal) sequence $〈c_ν〉$ with $c_ν ∈ \{+1, -1\}$, which is to be investigated starting in subtask (5). We are looking for its periodic auto-correlation function (PACF)
- $${\it \varphi}_{c}(\lambda) = {\rm E} \big [ c_\nu \cdot c_{\nu+\lambda} \big ] \hspace{0.05cm}.$$
In order to derive it, first the PACF
- $${\it \varphi}_{u}(\lambda) = {\rm E}\big [ u_\nu \cdot u_{\nu+\lambda} \big ]$$
with the unipolar coefficients $u_ν ∈ \{0, 1\}$, will be calculated. The conversion of the coefficients is given by $c_ν = 1 - 2u_ν$.
Note:
- The exercise belongs to the chapter Spreading Sequences for CDMA.
Questions
Solution
(2) Of the $P = 15$ spreading bits, $8$ are ones and $7$ are zeros. Thus, because $u_ν^{\hspace{0.04cm}2} = u_ν$:
- $${\rm E}\big [ u_\nu \big ] = {\rm E}\big [ u_\nu^2 \big ] = {8}/{15} \hspace{0.15cm}\underline {\approx 0.533} \hspace{0.05cm}, \hspace{0.3cm} \text{allgemein:}\,\, (P+1)/(2P)\hspace{0.05cm}.$$
(3) In bipolar representation, it is always $c_ν^{\hspace{0.04cm}2} = 1$. Thus, also for the quadratic expectation value:
- $${\rm E}\big [ c_\nu^{\hspace{0.04cm}2} \big ] \hspace{0.15cm}\underline {= 1}\hspace{0.05cm}.$$
(4) Solutions 1, 2 and 4 are correct:
- The attached table makes clear that for the discrete PACF values with $λ = 1$, ... , $14$ holds:
- $${\it \varphi}_{u}(\lambda) = {\rm E}\big [ u_\nu \cdot u_{\nu+\lambda} \big ]= {4}/{15} \hspace{0.05cm}.$$
- If we multiply 〈$u_ν$ 〉 with 〈$u_{ν+λ}$, where for the index $λ$ again the values $1$, ... , $14$ are to be used, then four ones occur in the product in each case.
- In contrast, for $λ = P = 15$:
- $${\it \varphi}_{u}(\lambda = 15) = {\rm E}\big [ u_\nu \cdot u_{\nu+P} \big ]= {8}/{15} \hspace{0.05cm}.$$
(5) The bipolar coefficients $c_ν$ result from the unipolar coefficients $u_ν$ according to the equation
- $$c_\nu = 1 - 2 \cdot u_\nu \hspace{0.3cm} \Rightarrow \hspace{0.3cm} u_\nu = 0\text{:} \ \ c_\nu = +1\hspace{0.05cm},\hspace{0.3cm}u_\nu = 1\text{:} \ \ c_\nu = -1 \hspace{0.05cm}.$$
- Thus, it follows from the calculation rules for expected values:
- $${\it \varphi}_{c}(\lambda) = {\rm E} \big [ c_\nu \cdot c_{\nu+\lambda} \big ]= {\rm E} \big [ (1 - 2 \cdot u_\nu ) \cdot (1 - 2 \cdot u_{\nu+\lambda} ) \big ] = 1 + 4 \cdot {\rm E}\big [ u_\nu \cdot u_{\nu+\lambda} \big ] - 2 \cdot {\rm E}\big [ u_\nu \big ] - 2 \cdot {\rm E}\big [ u_{\nu+\lambda} \big ] \hspace{0.05cm}.$$
- Using the result of subtask (2)
- $$ {\rm E}\left [ u_{\nu} \right ]= {\rm E}\left [ u_{\nu+\lambda} \right ]={8}/{15} \hspace{0.05cm},$$
and the subtask (4)
- $${\rm E}\big [ u_\nu \cdot u_{\nu+\lambda} \big ] ={4}/{15} \hspace{0.05cm} \,\,{\rm{f\ddot{u}r}}\,\,\lambda = 0, \pm P, \pm 2P, \text{...}$$
one thus arrives at the result $($if $λ$ is not a multiple of $P)$:
- $${\it \varphi}_{c}(\lambda) = 1 + 4 \cdot \frac{4}{15} - 2 \cdot \frac{8}{15}- 2 \cdot \frac{8}{15} = - \frac{1}{15} = - \frac{1}{P}\hspace{0.15cm}\underline {\approx - 0.067} \hspace{0.05cm}.$$
(6) A M-sequence with degree $G = 6$ has the period length $P = 63$.
- Corresponding to the result for subtask (5), we thus obtain:
- $$ {\it \varphi}_{c}(\lambda = 0) \hspace{0.15cm}\underline {= +1} \hspace{0.05cm},$$
- $$ {\it \varphi}_{c}(\lambda = 1)= - 1/63 \hspace{0.15cm}\underline {\approx - 0.016} \hspace{0.05cm},$$
- $$ {\it \varphi}_{c}(\lambda = 63) = {\it \varphi}_{c}(\lambda = 0) \hspace{0.15cm}\underline {= +1} \hspace{0.05cm},$$
- $$ {\it \varphi}_{c}(\lambda = 64) = {\it \varphi}_{c}(\lambda = 1)= - 1/63 \hspace{0.15cm}\underline {\approx - 0.016} \hspace{0.05cm}.$$