Aufgaben:Exercise 2.4: Frequency and Phase Offset

• Return to book

Model of a synchronous demodulator

Consider the source signal  $q(t) = A_{\rm 1} \cdot \cos(2 \pi f_{\rm 1} t ) +A_{\rm 2} \cdot \sin(2 \pi f_{\rm 2} t )$  with the signal parameters

$$A_1 = 2\,{\rm V}, \hspace{0.15cm}f_1 = 2\,{\rm kHz} \hspace{0.05cm},$$

$$A_2 = 1\,{\rm V}, \hspace{0.15cm}f_2 = 5\,{\rm kHz}\hspace{0.05cm}.$$

This signal is DSB amplitude-modulated.

• Thus,  the modulated signal  $s(t)$  has spectral components at  $±45$ kHz,  $±48$ kHz,  $±52$ kHz  and  $±55$ kHz. 
• It is also known,  that the transmitter-side carrier  $z(t)$  is sinusoidal  $(ϕ_{\rm T} = -90^\circ)$.

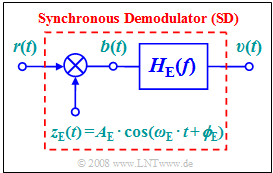
The demodulation to be performed with the circuit sketched here,  which is defined by the following parameters
("E"   ⇒   "empfägerseitig"   ⇒   "receiver-side"):

1.   Amplitude  $A_{\rm E}$  (no unit),
2.   frequency  $f_{\rm E}$,
3.   phase  $ϕ_{\rm E}$.

The  $H_{\rm E}(f)$  block represents an ideal,  rectangular low-pass filter,  which is suitably dimensioned.

Hints:

• This exercise belongs to the chapter  Synchronous Demodulation.
• Particular reference is made to the pages  Influence of a frequency offset  and  Influence of a phase offset.

• Take the following trigonometric transformations into account:

$$\cos(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) + \cos(\alpha+\beta)\right] \hspace{0.05cm},$$

$$\sin(\alpha)\cdot \cos(\beta) = {1}/{2} \cdot \left[ \sin(\alpha-\beta) + \sin(\alpha+\beta)\right] \hspace{0.05cm},$$

$$\sin(\alpha)\cdot \sin(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) - \cos(\alpha+\beta)\right] \hspace{0.05cm}.$$

Questions

1

Which of the following statements are true?

	The demodulator would work better for DSB-AM with carrier.
	The carrier would unnecessarily increase the transmit power.
	The correct dimensioning of the low-pass  $H_{\rm E}(f)$  is essential.
	One could also use an envelope demodulator.
	Envelope demodulation is only applicable for  $m \le 1$ .

2

How should the signal parameters of the receiver-side carrier signal  $z_{\rm E}(t)$  be chosen,  so that  $v(t) = q(t)$  holds?

$A_{\rm E} \ = \ $

$f_{\rm E} \ \hspace{0.05cm} = \ $ $\ \text{kHz}$

$\phi_{\rm E} \ = \ $ $\ \text{deg}$

3

Let  $f_{\rm E} = f_{\rm T}$  (no frequency offset).  Which sink signal  $v(t)$  results with  $ϕ_{\rm E} = - 120^\circ$?
Give its signal value at  $t = 0$ .

$v(t = 0)\ = \ $ $\ \text{V}$

4

Let  $f_{\rm E} = f_{\rm T}$  again.  Which sink signal  $v(t)$  results with  $ϕ_{\rm E} = 0^\circ$?
Give the signal value at  $t = 0$.

$v(t = 0)\ = \ $ $\ \text{V}$

5

Let  $ϕ_{\rm E} = ϕ_{\rm T}$  (no phase offset).  Which sink signal does one obtain with  $Δ\hspace{-0.05cm}f_{\rm T} = f_{\rm E} - f_{\rm T} = 1\text{ kHz}$?
Which of the following statements are correct?

	It holds that  $v(t) = q(t) · \cos(2π · Δ\hspace{-0.05cm}f_{\rm T} · t).$
	$v(t)$  contains a spectral component at  $2$ kHz.
	$v(t)$  contains a spectral component at $4$ kHz.
	$v(t)$  contains a spectral component at  $6$ kHz.

Solution

Solution

(1)  Answers 2, 3 and 5  are correct:

• Envelope demodulation is not applicable for DSB-AM without carrier and a modulation depth of   $m > 1$.
• The performance of the synchronous demodulator is not increased by the additional carrier component,  but only leads to an unnecessary increase in the transmit power to be applied.
• The third statement is also correct.  The solution to  Exercise 2.4Z  shows the effects of omitting or incorrectly dimensioning  $H_{\rm E} (f)$.

(2)  As the name  "synchronous demodulator"  already implies,  the signals   $z(t)$  and  $z_{\rm E} (t)$  must be synchronous in frequency and phase:

$$f_{\rm E} = f_{\rm T} \hspace{0.15cm}\underline {= 50\,{\rm kHz}}, \hspace{0.15cm}\phi_{\rm E} = \phi_{\rm T} \hspace{0.15cm}\underline {= - 90^{\circ}} \hspace{0.05cm}.$$

• The carrier frequency  $f_{\rm T}$  at the transmitter can be determined from the transmission spectrum  $S(f)$.  In the case of perfect synchronisation:

$$v(t) = {A_{\rm E}}/{2} \cdot q(t) + {A_{\rm E}}/{2} \cdot q(t)\cdot \cos(2 \cdot \omega_{\rm T} \cdot t ) \hspace{0.05cm}.$$

• The second term is removed by the low-pass filter.  Thus,  with  $A_{\rm E}\hspace{0.15cm}\underline{ = 2}$,  $v(t) = q(t)$ holds.

(3)  In the theory section,  it was shown that in general for DSB-AM and synchronous demodulation:

$$v(t) = \cos(\Delta \phi_{\rm T}) \cdot q(t) \hspace{0.05cm}.$$

• Even insufficient phase synchronisation does not lead to distortions,  only to a frequency-independent attenuation.
• With  $ϕ_{\rm T} =-90^\circ$  and  $ϕ_{\rm E} = -120^\circ$  ⇒   $Δϕ_{\rm T} = -30^\circ$:

$$v(t) = \cos(30^{\circ}) \cdot q(t)= 0.866 \cdot q(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} v(t= 0) = 0.866 \cdot A_1 \hspace{0.15cm}\underline {= 1.732\,{\rm V}}\hspace{0.05cm}.$$

(4)  Now the phase difference is   $Δϕ_{\rm T} = 90^\circ$  and we get  $v(t) \equiv 0$.

• It is pointless to discuss whether this is still a distortion-free system.
• The result  $v(t) \equiv 0$  is due to the fact that cosine and sine are orthogonal functions.
• This principle is made use of,  for example,  in what is known as   quadrature amplitude modulation..

(5)  The equation for the signal after multiplication is:

$$b(t) = q(t) \cdot \cos(\omega_{\rm T} \cdot t - 90^{\circ}) \cdot 2 \cdot \cos(\omega_{\rm E} \cdot t - 90^{\circ})= 2 \cdot q(t) \cdot \sin(\omega_{\rm T} \cdot t ) \cdot \sin(\omega_{\rm E} \cdot t )\hspace{0.05cm}.$$

• This result can also be rewritten using the trigonometric transformation

$$\sin(\alpha)\cdot \sin(\beta) = {1}/{2} \cdot \left[ \cos(\alpha-\beta) - \cos(\alpha+\beta)\right]$$

as follows:

$$b(t) = q(t) \cdot \cos((\omega_{\rm T} - \omega_{\rm E}) \cdot t ) + q(t) \cdot \cos((\omega_{\rm T} + \omega_{\rm E}) \cdot t ) \hspace{0.05cm}.$$

• The second term lies in the vicinity of   $2f_{\rm T}$  for   $f_{\rm E} = f_{\rm T}$  and is removed by the low-pass.
• With the frequency difference   $Δ\hspace{-0.05cm}f_{\rm T} = f_{\rm E} - f_{\rm T}= 1$ kHz,  this leaves:

$$v(t) = q(t) \cdot \cos(2 \pi \cdot \Delta \hspace{-0.05cm}f_{\rm T} \cdot t) \hspace{0.05cm}.$$

• The first statement is correct.  This states that now the signal   $v(t)$  becomes quieter and louder again after demodulation according to a cosine function  (a  "beat").
• The cosine component of   $q(t)$  with frequency   $f_1 = 2\text{ kHz}$  now becomes two components  (each of half the amplitude)  at   $1\text{ kHz}$ and $3\text{ kHz}$.
• Similarly,  the sink signal does not include a component at  $f_2 = 5\text{ kHz}$,  only components at   $4\text{ kHz}$  and at  $6\text{ kHz}$:

$$1\,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t)\cdot \cos(2 \pi \cdot 1\,{\rm kHz} \cdot t) = 0.5\,{\rm V} \cdot \sin(2 \pi \cdot 4\,{\rm kHz} \cdot t) + 0.5\,{\rm V} \cdot \sin(2 \pi \cdot 6\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$

Answers 1, 3 and 4  are correct.