Difference between revisions of "Aufgaben:Exercise 3.3Z: Moments for Triangular PDF"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID142__Sto_Z_3_3.png|right|frame| | + | [[File:P_ID142__Sto_Z_3_3.png|right|frame|Two triangular PDF]] |
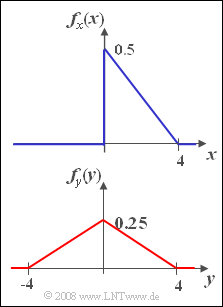
| − | + | We consider in this task two random signals $x(t)$ and $y(t)$ each with triangular PDF, namely | |
| − | * | + | * the one-sided triangular PDF according to the upper graph: |
| − | :$$f_x(x)=\left\{ \begin{array}{*{4}{c}} | + | :$$f_x(x)=\left\{ \begin{array}{*{4}{c}} 0.5 \cdot (1-{ x}/{\rm 4}) & \rm f\ddot{u}r\hspace{0.2cm}{\rm 0 \le {\it x} \le 4},\rm 0 & \rm else. \end{array} \right.$$ |
| − | * | + | * the two-sided triangular PDF according to the graph below: |
| − | :$$ f_y(y)=\left\{ \begin{array}{*{4}{c}} 0.25 \cdot (1-{ |y|}/{\rm 4}) & \rm f\ddot{u}r\hspace{0.2cm}{ -4 \le {\it y} \le \rm 4}, | + | :$$ f_y(y)=\left\{ \begin{array}{*{4}{c}} 0.25 \cdot (1-{ |y|}/{\rm 4}) & \rm f\ddot{u}r\hspace{0.2cm}{ -4 \le {\it y} \le \rm 4},\rm 0 & \rm else. \end{array} \right.$$ |
| − | + | To solve this problem, consider the equation for the central moments: | |
:$$\mu_k=\sum\limits_{\kappa = \rm 0}^{\it k}\left({k} \atop {\kappa}\right)\cdot m_k\cdot(-m_{\rm 1})^{k - \kappa}.$$ | :$$\mu_k=\sum\limits_{\kappa = \rm 0}^{\it k}\left({k} \atop {\kappa}\right)\cdot m_k\cdot(-m_{\rm 1})^{k - \kappa}.$$ | ||
| − | + | Specifically, this equation yields the following results: | |
:$$\mu_{\rm 1}=0,\hspace{0.5cm}\mu_{\rm 2}=\it m_{\rm 2}-\it m_{\rm 1}^{\rm 2},\hspace{0.5cm}\mu_{\rm 3}=\it m_{\rm 3}-\rm 3\cdot\it m_{\rm 2}\cdot \it m_{\rm 1} {\rm +}\rm 2\cdot\it m_{\rm 1}^{\rm 3},$$ | :$$\mu_{\rm 1}=0,\hspace{0.5cm}\mu_{\rm 2}=\it m_{\rm 2}-\it m_{\rm 1}^{\rm 2},\hspace{0.5cm}\mu_{\rm 3}=\it m_{\rm 3}-\rm 3\cdot\it m_{\rm 2}\cdot \it m_{\rm 1} {\rm +}\rm 2\cdot\it m_{\rm 1}^{\rm 3},$$ | ||
:$$\mu_{\rm 4}=\it m_{\rm 4}-\rm 4\cdot\it m_{\rm 3}\cdot \it m_{\rm 1}\rm +6\cdot\it m_{\rm 2}\cdot\it m_{\rm 1}^{\rm 2}-\rm 3\cdot\it m_{\rm 1}^{\rm 4}.$$ | :$$\mu_{\rm 4}=\it m_{\rm 4}-\rm 4\cdot\it m_{\rm 3}\cdot \it m_{\rm 1}\rm +6\cdot\it m_{\rm 2}\cdot\it m_{\rm 1}^{\rm 2}-\rm 3\cdot\it m_{\rm 1}^{\rm 4}.$$ | ||
| − | + | From the central moments of higher order one can derive, among others: | |
| − | * | + | *the "Charlier's skewness</i>" $S = {\mu_3}/{\sigma^3}\hspace{0.05cm},$ |
| − | * | + | *the "Kurtosis</i>" $K = {\mu_4}/{\sigma^4}\hspace{0.05cm}.$ |
| Line 31: | Line 31: | ||
| − | + | Hints: | |
| − | * | + | *This exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Erwartungswerte_und_Momente|Erwartungswerte und Momente]]. |
| − | * | + | *Reference is made to the page [[Theory_of_Stochastic_Signals/Expected_Values_and_Moments#Some_common_central_moments|Some common central moments]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate from the present PDF $f_x(x)$ the moment $k$-th order. <br>What value results for the linear mean $m_x = m_1$? |
|type="{}"} | |type="{}"} | ||
| − | $m_x \ = \ $ | + | $m_x \ = \ $ { 1.333 3% } |
| − | { | + | {What is the quadratic mean and the rms $\sigma_x$ of the random variable $x$? |
|type="{}"} | |type="{}"} | ||
$\sigma_x\ = \ $ { 0.943 3% } | $\sigma_x\ = \ $ { 0.943 3% } | ||
| − | { | + | {For random variable $x$ how large is Charlier's skewness $S_x = \mu_3/\sigma_x^3$? Why is $S_x \ne 0$? |
|type="{}"} | |type="{}"} | ||
$S_x \ = \ $ { 0.566 3% } | $S_x \ = \ $ { 0.566 3% } | ||
| − | { | + | {Which statements are true for the symmetrically distributed random variable $y$ ? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + All moments with odd $k$ are $m_k =0$. |
| − | - | + | - All moments with even $k$ are $m_k =0$. |
| − | + | + | + All moments $m_k$ with even $k$ are calculated as in subtask '''(1)''' . |
| − | + | + | + The central moments $\mu_k$ are equal to the non-centered moments $m_k$. |
| − | { | + | {Calculate the rms of the random variable $y$. |
|type="{}"} | |type="{}"} | ||
$\sigma_y \ = \ $ { 1.633 3% } | $\sigma_y \ = \ $ { 1.633 3% } | ||
| − | { | + | {What value is obtained for the kurtosis $K_y$ of the random variable $y$? Interpret the result. |
|type="{}"} | |type="{}"} | ||
$K_y \ = \ $ { 2.4 3% } | $K_y \ = \ $ { 2.4 3% } | ||
| Line 77: | Line 77: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' For the $k$–th order moment of the random variable $x$ holds: |
| − | :$$m_k=1/2\cdot | + | :$$m_k=1/2\cdot \int_{\rm 0}^{\rm 4} x^k\cdot ( 1-\frac{\it x}{\rm 4}) \hspace{0.1cm}{\rm d}x.$$ |
| − | * | + | *This leads to the result: |
:$$m_k=\frac{x^{ k+ 1}}{ 2\cdot ( k+ 1)}\Bigg|_{\rm 0}^{\rm 4}-\frac{x^{ k+2}}{8\cdot ( k+2)}\Bigg|_{\rm 0}^{\rm 4}=\frac{\rm 2\cdot \rm 4^{\it k}}{(\it k\rm +1)\cdot (\it k\rm + 2)}.$$ | :$$m_k=\frac{x^{ k+ 1}}{ 2\cdot ( k+ 1)}\Bigg|_{\rm 0}^{\rm 4}-\frac{x^{ k+2}}{8\cdot ( k+2)}\Bigg|_{\rm 0}^{\rm 4}=\frac{\rm 2\cdot \rm 4^{\it k}}{(\it k\rm +1)\cdot (\it k\rm + 2)}.$$ | ||
| − | * | + | *From this we obtain for the linear mean $(k= 1)$: |
:$$m_x=\rm {4}/{3}\hspace{0.15cm}\underline{=1.333}.$$ | :$$m_x=\rm {4}/{3}\hspace{0.15cm}\underline{=1.333}.$$ | ||
| − | '''(2)''' | + | '''(2)''' The $(k= 2)$ is $m_2 = 8/3$. |
| − | * | + | *From this follows with <i>Steiner's theorem</i>: |
:$$\sigma_x^{\rm 2}={8}/{3}-({4}/{3})^2=\rm {8}/{9}\hspace{0.5cm}\Rightarrow\hspace{0.5cm} \sigma_x\hspace{0.15cm}\underline{\approx \rm 0.943}.$$ | :$$\sigma_x^{\rm 2}={8}/{3}-({4}/{3})^2=\rm {8}/{9}\hspace{0.5cm}\Rightarrow\hspace{0.5cm} \sigma_x\hspace{0.15cm}\underline{\approx \rm 0.943}.$$ | ||
| − | '''(3)''' | + | '''(3)''' With $m_1 = 4/3$, $m_2 = 8/3$ and $m_3 = 32/5$ , the given equation for the third order central moment gives: $\mu_3 = 64/135 \approx 0.474$. |
| − | * | + | *From this follows for <i>Charlier's skewness</i>: |
:$$S_x=\rm \frac{64/135}{\Big(\sqrt {8/9}\Big)^3}=\frac{\sqrt{8}}{5}\hspace{0.15cm}\underline{\approx 0.566}.$$ | :$$S_x=\rm \frac{64/135}{\Big(\sqrt {8/9}\Big)^3}=\frac{\sqrt{8}}{5}\hspace{0.15cm}\underline{\approx 0.566}.$$ | ||
| − | * | + | *Due to the asymmetric PDF, $S_x \ne 0$. |
| − | '''(4)''' | + | '''(4)''' Correct are <u>the proposed solutions 1, 3 and 4</u>: |
| − | * | + | *For symmetric PDF, all odd moments are zero, including the mean $m_y$. |
| − | * | + | *Therefore, in terms of randomness $y$ there is no difference between the moments $m_k$ and the central moments $\mu_k$. |
| − | * | + | *The moments $m_k$ with even $k$ are the same for the random variables $x$ and $y$ . This is evident from the time averages. |
| − | * | + | *Since $x^2(t) = y^2(t)$, for $k = 2n$ the moments are also equal: |
:$$m_k=m_{2 n}=\ \text{...}\int [x^2(t)]^n \hspace{0.1cm}{\rm d} x=\ \text{...}\int [y^2(t)]^n \hspace{0.1cm}{\rm d} y.$$ | :$$m_k=m_{2 n}=\ \text{...}\int [x^2(t)]^n \hspace{0.1cm}{\rm d} x=\ \text{...}\int [y^2(t)]^n \hspace{0.1cm}{\rm d} y.$$ | ||
| − | '''(5)''' | + | '''(5)''' With the result of the subtask '''(2)''' holds: |
:$$m_2=\mu_{\rm 2}=\sigma_y^2=\rm {8}/{3} = 2.667\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_y\hspace{0.15cm}\underline{=1.633}.$$ | :$$m_2=\mu_{\rm 2}=\sigma_y^2=\rm {8}/{3} = 2.667\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_y\hspace{0.15cm}\underline{=1.633}.$$ | ||
| − | '''(6)''' | + | '''(6)''' The fourth-order central moment is equal to the moment $m_4$ for symmetric WDF. |
| − | * | + | *From the general equation calculated in subtask '''(1)''' one obtains $\mu_4 = 256/15.$ |
| − | * | + | *From this follows for the kurtosis: |
:$$K_y=\frac{\mu_{\rm 4}}{\sigma_y^{\rm 4}}=\rm \frac{256/15}{(8/3)^2}\hspace{0.15cm}\underline{=2.4}.$$ | :$$K_y=\frac{\mu_{\rm 4}}{\sigma_y^{\rm 4}}=\rm \frac{256/15}{(8/3)^2}\hspace{0.15cm}\underline{=2.4}.$$ | ||
| − | ::'' | + | ::''Note:'' This numerical value is valid for the triangle WDF in general and lies between the kurtosis values of uniform distribution $(K = 1.8)$ and Gaussian distribution $(K = 3)$. This is a quantitative evaluation of the fact that here |
| − | ::* | + | ::*the outliers are more pronounced than in the case of a uniformly distributed random size, |
| − | ::* | + | ::*but due to the limitation less pronounced than with Gaussian sizes. |
| − | + | Then we will prove that the asymmetric triangular WDF $f_x(x)$ also has the same kurtosis as shown in the upper sketch on the data sheet: | |
| − | :$$\mu_{ 4} = m_{\rm 4}- 4\cdot m_{\rm 3}\cdot | + | : $$\mu_{ 4} = m_{\rm 4}- 4\cdot m_{\rm 3}\cdot m_{\rm 1}+ 6\cdot m_{\rm 2}\cdot m_{\rm 1}^{\rm 2}- 3\cdot m_{\rm 1}^{\rm 4}= \frac{256}{15} - 4 \cdot \frac{32}{5}\cdot \frac{4}{3} + 6 \cdot \frac{8}{3}\cdot \left(\frac{4}{3}\right)^2 -3 \cdot \left(\frac{4}{3}\right)^4 =\frac{256}{15 \cdot 9}$$ |
| − | * | + | *With the result of the subtask '''(3)''' ⇒ $\sigma_x^2 = 8/9$ it follows: |
| − | :$$ | + | :$$ K_x = \frac{{256}/(15 \cdot 9)}{8/9 \cdot 8/9} = 2.4.$$ |
Revision as of 02:20, 28 December 2021
We consider in this task two random signals $x(t)$ and $y(t)$ each with triangular PDF, namely
- the one-sided triangular PDF according to the upper graph:
- $$f_x(x)=\left\{ \begin{array}{*{4}{c}} 0.5 \cdot (1-{ x}/{\rm 4}) & \rm f\ddot{u}r\hspace{0.2cm}{\rm 0 \le {\it x} \le 4},\rm 0 & \rm else. \end{array} \right.$$
- the two-sided triangular PDF according to the graph below:
- $$ f_y(y)=\left\{ \begin{array}{*{4}{c}} 0.25 \cdot (1-{ |y|}/{\rm 4}) & \rm f\ddot{u}r\hspace{0.2cm}{ -4 \le {\it y} \le \rm 4},\rm 0 & \rm else. \end{array} \right.$$
To solve this problem, consider the equation for the central moments:
- $$\mu_k=\sum\limits_{\kappa = \rm 0}^{\it k}\left({k} \atop {\kappa}\right)\cdot m_k\cdot(-m_{\rm 1})^{k - \kappa}.$$
Specifically, this equation yields the following results:
- $$\mu_{\rm 1}=0,\hspace{0.5cm}\mu_{\rm 2}=\it m_{\rm 2}-\it m_{\rm 1}^{\rm 2},\hspace{0.5cm}\mu_{\rm 3}=\it m_{\rm 3}-\rm 3\cdot\it m_{\rm 2}\cdot \it m_{\rm 1} {\rm +}\rm 2\cdot\it m_{\rm 1}^{\rm 3},$$
- $$\mu_{\rm 4}=\it m_{\rm 4}-\rm 4\cdot\it m_{\rm 3}\cdot \it m_{\rm 1}\rm +6\cdot\it m_{\rm 2}\cdot\it m_{\rm 1}^{\rm 2}-\rm 3\cdot\it m_{\rm 1}^{\rm 4}.$$
From the central moments of higher order one can derive, among others:
- the "Charlier's skewness" $S = {\mu_3}/{\sigma^3}\hspace{0.05cm},$
- the "Kurtosis" $K = {\mu_4}/{\sigma^4}\hspace{0.05cm}.$
Hints:
- This exercise belongs to the chapter Erwartungswerte und Momente.
- Reference is made to the page Some common central moments.
Questions
Solution
- $$m_k=1/2\cdot \int_{\rm 0}^{\rm 4} x^k\cdot ( 1-\frac{\it x}{\rm 4}) \hspace{0.1cm}{\rm d}x.$$
- This leads to the result:
- $$m_k=\frac{x^{ k+ 1}}{ 2\cdot ( k+ 1)}\Bigg|_{\rm 0}^{\rm 4}-\frac{x^{ k+2}}{8\cdot ( k+2)}\Bigg|_{\rm 0}^{\rm 4}=\frac{\rm 2\cdot \rm 4^{\it k}}{(\it k\rm +1)\cdot (\it k\rm + 2)}.$$
- From this we obtain for the linear mean $(k= 1)$:
- $$m_x=\rm {4}/{3}\hspace{0.15cm}\underline{=1.333}.$$
(2) The $(k= 2)$ is $m_2 = 8/3$.
- From this follows with Steiner's theorem:
- $$\sigma_x^{\rm 2}={8}/{3}-({4}/{3})^2=\rm {8}/{9}\hspace{0.5cm}\Rightarrow\hspace{0.5cm} \sigma_x\hspace{0.15cm}\underline{\approx \rm 0.943}.$$
(3) With $m_1 = 4/3$, $m_2 = 8/3$ and $m_3 = 32/5$ , the given equation for the third order central moment gives: $\mu_3 = 64/135 \approx 0.474$.
- From this follows for Charlier's skewness:
- $$S_x=\rm \frac{64/135}{\Big(\sqrt {8/9}\Big)^3}=\frac{\sqrt{8}}{5}\hspace{0.15cm}\underline{\approx 0.566}.$$
- Due to the asymmetric PDF, $S_x \ne 0$.
(4) Correct are the proposed solutions 1, 3 and 4:
- For symmetric PDF, all odd moments are zero, including the mean $m_y$.
- Therefore, in terms of randomness $y$ there is no difference between the moments $m_k$ and the central moments $\mu_k$.
- The moments $m_k$ with even $k$ are the same for the random variables $x$ and $y$ . This is evident from the time averages.
- Since $x^2(t) = y^2(t)$, for $k = 2n$ the moments are also equal:
- $$m_k=m_{2 n}=\ \text{...}\int [x^2(t)]^n \hspace{0.1cm}{\rm d} x=\ \text{...}\int [y^2(t)]^n \hspace{0.1cm}{\rm d} y.$$
(5) With the result of the subtask (2) holds:
- $$m_2=\mu_{\rm 2}=\sigma_y^2=\rm {8}/{3} = 2.667\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_y\hspace{0.15cm}\underline{=1.633}.$$
(6) The fourth-order central moment is equal to the moment $m_4$ for symmetric WDF.
- From the general equation calculated in subtask (1) one obtains $\mu_4 = 256/15.$
- From this follows for the kurtosis:
- $$K_y=\frac{\mu_{\rm 4}}{\sigma_y^{\rm 4}}=\rm \frac{256/15}{(8/3)^2}\hspace{0.15cm}\underline{=2.4}.$$
- Note: This numerical value is valid for the triangle WDF in general and lies between the kurtosis values of uniform distribution $(K = 1.8)$ and Gaussian distribution $(K = 3)$. This is a quantitative evaluation of the fact that here
- the outliers are more pronounced than in the case of a uniformly distributed random size,
- but due to the limitation less pronounced than with Gaussian sizes.
- Note: This numerical value is valid for the triangle WDF in general and lies between the kurtosis values of uniform distribution $(K = 1.8)$ and Gaussian distribution $(K = 3)$. This is a quantitative evaluation of the fact that here
Then we will prove that the asymmetric triangular WDF $f_x(x)$ also has the same kurtosis as shown in the upper sketch on the data sheet:
- $$\mu_{ 4} = m_{\rm 4}- 4\cdot m_{\rm 3}\cdot m_{\rm 1}+ 6\cdot m_{\rm 2}\cdot m_{\rm 1}^{\rm 2}- 3\cdot m_{\rm 1}^{\rm 4}= \frac{256}{15} - 4 \cdot \frac{32}{5}\cdot \frac{4}{3} + 6 \cdot \frac{8}{3}\cdot \left(\frac{4}{3}\right)^2 -3 \cdot \left(\frac{4}{3}\right)^4 =\frac{256}{15 \cdot 9}$$
- With the result of the subtask (3) ⇒ $\sigma_x^2 = 8/9$ it follows:
- $$ K_x = \frac{{256}/(15 \cdot 9)}{8/9 \cdot 8/9} = 2.4.$$