Aufgaben:Exercise 3.6: Noisy DC Signal

• Return to book

Noise DC signal and WDF

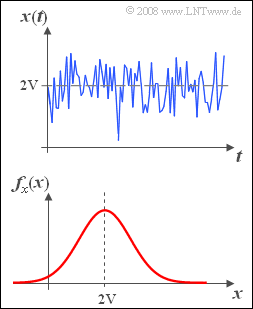
A DC signal  $s(t) = 2\hspace{0.05cm}\rm V$  is additively overlaid by a noise signal  $n(t)$  .

• In the upper picture you can see a section of the sum signal   $x(t)=s(t)+n(t).$
• The probability density function (PDF) of the signal  $x(t)$  is shown below.
• The  (related to the resistor  $1\hspace{0.05cm} \Omega$  total power of this signal is  $P_x = 5\hspace{0.05cm}\rm V^2$.

Hints:

• The exercise belongs to the chapter  Gaussian Distributed Random Variable.
• Use the  complementary Gaussian error integral  ${\rm Q}(x)$ to solve.
• The following are some values of this monotonically decreasing function:

$$\rm Q(0) = 0.5,\hspace{0.5cm} Q(1) = 0.1587, \hspace{0.5cm}\rm Q(2) = 0.0227, \hspace{0.5cm} Q(3) = 0.0013. $$

Questions

1

Which of the following statements are true?

	The signal $s(t)$  is uniformly distributed.
	The noise signal  $n(t)$  is Gaussian distributed.
	The noise signal  $n(t)$  has a mean value  $m_n \ne 0$.
	The total signal  $x(t)$  is Gaussian distributed with mean  $m_x = 2\hspace{0.05cm}\rm V$.

2

Calculate the standard deviation (rms) of the signal  $x(t)$.

$\sigma_x \ = \ $ $\ \rm V$

3

What is the probability that $x(t) < 0\hspace{0.05cm}\rm V$  ?

${\rm Pr}(x < 0\hspace{0.05cm}\rm V)\ = \ $ $\ \%$

4

What is the probability that  $x(t) > 4\hspace{0.05cm}\rm V$  ?

${\rm Pr}(x > 4\hspace{0.05cm}\rm V)\ = \ $ $\ \%$

5

What is the probability  $x(t)$  between  $3\hspace{0.05cm}\rm V$  and  $4\hspace{0.05cm}\rm V$?

${\rm Pr}(+3\hspace{0.05cm}{\rm V} < x < +4\hspace{0.05cm}{\rm V}) \ = \ $ $\ \%$

Solution

Solution

(1)  Correct are solutions 2 and 4:

• The uniform signal  $s(t)$  is not uniformly distributed, rather its PDF consists of only one Dirac function at  $m_x = 2\hspace{0.05cm}\rm V$  with weight  $1$.
• The signal  $n(t)$  is gaussian and mean-free   ⇒   $m_n = 0$.
• Therefore the sum signal  $x(t)$  is also Gaussian, but now with mean  $m_x = 2\hspace{0.05cm}\rm V$.
• This is due to the DC signal alone  $s(t) = 2\hspace{0.05cm}\rm V$ .

(2)  According to Steiner's theorem:

$$\sigma_{x}^{\rm 2}=m_{\rm 2 \it x}-m_{x}^{\rm 2}. $$

• The quadratic mean  $m_{2x}$  is equal to the  $($referred$to  $1\hspace{0.05cm} \Omega$  total power  $P_x = 5\hspace{0.05cm}\rm V^2$. *With the mean  $m_x = 2\hspace{0.05cm}\rm V$  it follows for the dispersion:   :'"`UNIQ-MathJax23-QINU`"' '''(3)'''  The distribution function (CDF) of a Gaussian random grö&airst;e  $($mean  $m_x$,  scatter $\sigma_x)$  is with the Gaussian error integral: :'"`UNIQ-MathJax24-QINU`"' *The distribution function at the point  $r = 0\hspace{0.05cm}\rm V$  is equal to the probability that  $x$  is less than or equal to  $0\hspace{0.05cm}\rm V$ . *But for continuous random variables, ${\rm Pr}(x \le r) = {\rm Pr}(x < r)$ also holds . *Using the complementary Gaussian error integral, we obtain: :'"`UNIQ-MathJax25-QINU`"' '''(4)'''  Because of the symmetry around the mean  $m_x = 2\hspace{0.05cm}\rm V$  this gives the same probability, viz. :'"`UNIQ-MathJax26-QINU`"' '''(5)'''  The probability that  $x$  is greater than  $3\hspace{0.05cm}\rm V$ is given by.

$${\rm Pr}( x > 3\text{ V}) = 1- F_x(\frac{3\text{ V}-2\text{ V}}{1\text{ V}})=\rm Q(\rm 1)=\rm 0.1587.$$

• For the sought probability one obtains from it:

$$\rm Pr(3\,V\le \it x \le \rm 4\,V)= \rm Pr(\it x > \rm 3\,V)- \rm Pr(\it x > \rm 4\,V) = 0.1587 - 0.0227\hspace{0.15cm}\underline{=\rm 13.6\%}. $$