Difference between revisions of "Aufgaben:Exercise 4.16: Eigenvalues and Eigenvectors"
m (Guenter moved page Aufgabe 4.16: Eigenwerte und Eigenvektoren to Exercise 4.16: Eigenvalues and Eigenvectors) |
|||
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Theory_of_Stochastic_Signals/Generalization_to_N-Dimensional_Random_Variables |
}} | }} | ||
| − | [[File:P_ID671__Sto_A_4_16.png|right|frame| | + | [[File:P_ID671__Sto_A_4_16.png|right|frame|Three correlation matrices]] |
| − | + | Although the description of Gaussian random variables using vectors and matrices is actually only necessary and makes sense for more than $N = 2$ dimensions, here we restrict ourselves to the special case of two-dimensional random variables for simplicity. | |
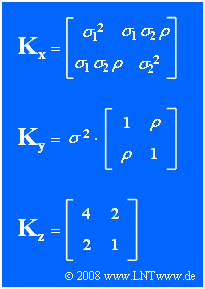
| − | In | + | In the graph above, the general correlation matrix $\mathbf{K_x}$ of the 2D–random variable $\mathbf{x} = (x_1, x_2)^{\rm T}$ is given, where $\sigma_1^2$ and $\sigma_2^2$ describe the variances of the individual components. $\rho$ denotes the correlation coefficient between the two components. |
| − | + | The random variables $\mathbf{y}$ and $\mathbf{z}$ give two special cases of $\mathbf{x}$ whose process parameters are to be determined from the correlation matrices $\mathbf{K_y}$ and $\mathbf{K_z}$ respectively. | |
| Line 19: | Line 19: | ||
| − | + | Hints: | |
| − | * | + | *The exercise belongs to the chapter [[Theory_of_Stochastic_Signals/Generalization_to_N-Dimensional_Random_Variables|Generalization to N-Dimensional Random Variables]]. |
| − | * | + | *Some basics on the application of vectors and matrices can be found on the pages [[Theory_of_Stochastic_Signals/Generalization_to_N-Dimensional_Random_Variables#Basics_of_matrix_operations:_Determinant_of_a_matrix|Determinant of a Matrix]] and [[Theory_of_Stochastic_Signals/Generalization_to_N-Dimensional_Random_Variables#Basics_of_matrix_operations:_Inverse_of_a_matrix|Inverse of a Matrix]] . |
| − | * | + | * According to the page [[Theory_of_Stochastic_Signals/Two-Dimensional_Gaussian_Random_Variables#Contour_lines_for_correlated_random_variables|Contour lines for correlated random variables]] the angle $\alpha$ between the old and the new system is given by the following equation: |
:$$\alpha = {1}/{2}\cdot \arctan (2 \cdot\rho \cdot | :$$\alpha = {1}/{2}\cdot \arctan (2 \cdot\rho \cdot | ||
\frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2}).$$ | \frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2}).$$ | ||
| − | * | + | *In particular, note: |
| − | ** | + | **A $2×2$-covariance matrix has two real eigenvalues $\lambda_1$ and $\lambda_2$. |
| − | ** | + | **These two eigenvalues determine two eigenvectors $\xi_1$ and $\xi_2$. |
| − | ** | + | **These span a new coordinate system in the direction of the principal axes of the old system. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are true for the correlation matrix $\mathbf{K_y}$ ? |
|type="[]"} | |type="[]"} | ||
| − | + $\mathbf{K_y}$ | + | + $\mathbf{K_y}$ describes all possible two-dimensional random variables with $\sigma_1 = \sigma_2 = \sigma$. |
| − | + | + | + The value range of the parameter $\rho$ is $-1 \le \rho \le +1$. |
| − | - | + | - The value range of the parameter $\rho$ is $0 < \rho < 1$. |
| − | { | + | {Calculate the eigenvalues of $\mathbf{K_y}$ under the condition $\sigma = 1$ and $\rho = 0$. |
|type="{}"} | |type="{}"} | ||
$\lambda_1 \ = \ $ { 1 3% } $\ (\lambda_1 \ge \lambda_2)$ | $\lambda_1 \ = \ $ { 1 3% } $\ (\lambda_1 \ge \lambda_2)$ | ||
| − | $\lambda_2 \ = \ | + | $\lambda_2 \ = \ $ { 1 3% } $\ (\lambda_2 \le \lambda_1)$ |
| − | { | + | {Give the eigenvalues of $\mathbf{K_y}$ under the condition $\sigma = 1$ and $0 < \rho < 1$ What values result for $\rho = 0.5 $, assuming $\lambda_1 \ge \lambda_2$ ? |
|type="{}"} | |type="{}"} | ||
| − | $\lambda_1 \ = | + | $\lambda_1 \ = \ $ { 1.5 3% } $\ (\lambda_1 \ge \lambda_2)$ |
| − | $\lambda_2 \ = | + | $\lambda_2 \ = \ $ { 0.5 3% } $\ (\lambda_2 \le \lambda_1)$ |
| − | { | + | {Calculate the corresponding eigenvectors $\mathbf{\eta_1}$ and $\mathbf{\eta_2}$. Which of the following statements are true? |
|type="[]"} | |type="[]"} | ||
| − | + $\mathbf{\eta_1}$ | + | + $\mathbf{\eta_1}$ and $\mathbf{\eta_2}$ lie in the direction of the ellipse principal axes. |
| − | + | + | + The new coordinates are rotated by $45^\circ$ . |
| − | - | + | - The scatterings with respect to the new system are $\lambda_1$ and $\lambda_2$. |
| − | { | + | {What are the characteristics of the random variable specified by $\mathbf{K_z}$ $\mathbf{z}$? |
|type="{}"} | |type="{}"} | ||
$\sigma_1 = \ $ { 2 3% } | $\sigma_1 = \ $ { 2 3% } | ||
| Line 68: | Line 68: | ||
| − | { | + | {Calculate the eigenvalues $\lambda_1$ and $\lambda_2 \le \lambda_1$ of the correlation matrix $\mathbf{K_z}$. |
|type="{}"} | |type="{}"} | ||
| − | $\lambda_1 \ = \ | + | $\lambda_1 \ = \ $ { 5 3% } $\ (\lambda_1 \ge \lambda_2)$ |
| − | $\lambda_2 \ = \ | + | $\lambda_2 \ = \ $ { 0. } $\ (\lambda_2 \le \lambda_1)$ |
| − | { | + | {By what angle $\alpha$ is the new coordinate system $(\mathbf{\zeta_1}, \ \mathbf{\zeta_2})$ rotated with respect to the original system $(\mathbf{z_1}, \ \mathbf{z_2})$ ? |
|type="{}"} | |type="{}"} | ||
| − | $\alpha \ = | + | $\alpha \ = \ $ { 26.56 3% } $\ \rm deg$ |
| Line 82: | Line 82: | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are <u>proposed solutions 1 and 2</u>: |
| − | *$\mathbf{K_y}$ | + | *$\mathbf{K_y}$ is indeed the most general correlation matrix of a 2D random variable with $\sigma_1 = \sigma_2 = \sigma$. |
| − | * | + | *The parameter $\rho$ specifies the correlation coefficient. This can take all values between $\pm 1$ including these marginal values. |
| − | '''(2)''' In | + | '''(2)''' In this case, the governing equation is: |
:$${\rm det}\left[ \begin{array}{cc} | :$${\rm det}\left[ \begin{array}{cc} | ||
| − | 1- \lambda & 0 | + | 1- \lambda & 0 \ |
0 & 1- \lambda | 0 & 1- \lambda | ||
\end{array} \right] = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \end{array} \right] = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| − | (1- \lambda)^2 | + | (1- \lambda)^2 = 0\hspace{0.3cm}\Rightarrow |
\hspace{0.3cm} \hspace{0.15cm}\underline{\lambda_{1/2} =1}.$$ | \hspace{0.3cm} \hspace{0.15cm}\underline{\lambda_{1/2} =1}.$$ | ||
| − | '''(3)''' | + | '''(3)''' With positive $\rho$ the governing equation of the eigenvalues is: |
:$$(1- \lambda)^2 -\rho^2 = 0\hspace{0.5cm}\Rightarrow | :$$(1- \lambda)^2 -\rho^2 = 0\hspace{0.5cm}\Rightarrow | ||
\hspace{0.5cm}\lambda^2 - 2\lambda + 1 - \rho^2 = | \hspace{0.5cm}\lambda^2 - 2\lambda + 1 - \rho^2 = | ||
0\hspace{0.5cm}\Rightarrow\hspace{0.5cm}\lambda_{1/2} =1 \pm \rho.$$ | 0\hspace{0.5cm}\Rightarrow\hspace{0.5cm}\lambda_{1/2} =1 \pm \rho.$$ | ||
| − | * | + | *For $\rho= 0.5$ one gets $\underline{\lambda_{1} =1.5}$ and $\underline{\lambda_{2} =0.5}$. |
| − | * | + | *By the way, the equation holds in the whole domain of definition $-1 \le \rho \le +1$. |
| − | * | + | *For $\rho = 0$ is $\lambda_1 = \lambda_2 = +1$ ⇒ see subtask '''(2)''''. |
| − | * | + | *For $\rho = \pm 1$ this gives $\lambda_1 = 2$ and $\lambda_2 = 0$. |
| − | '''(4)''' | + | '''(4)''' The eigenvectors are obtained by substituting the eigenvalues $\lambda_1$ and $\lambda_2$ into the correlation matrix: |
:$$\left[ \begin{array}{cc} | :$$\left[ \begin{array}{cc} | ||
1- (1+\rho) & \rho \\ | 1- (1+\rho) & \rho \\ | ||
| Line 150: | Line 150: | ||
\end{array} \right].$$ | \end{array} \right].$$ | ||
| − | [[File:P_ID676__Sto_A_4_16_d.png|right|frame| | + | [[File:P_ID676__Sto_A_4_16_d.png|right|frame|To rotate the coordinate system]] |
| − | + | Putting this into what is called orthonormal form, the following holds: | |
:$${\boldsymbol{\eta_1}}= \frac{1}{\sqrt{2}}\cdot \left[ | :$${\boldsymbol{\eta_1}}= \frac{1}{\sqrt{2}}\cdot \left[ | ||
\begin{array}{c} | \begin{array}{c} | ||
| Line 163: | Line 163: | ||
\end{array} \right].$$ | \end{array} \right].$$ | ||
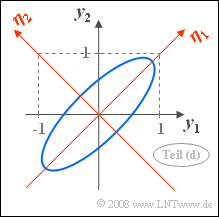
| − | + | The sketch illustrates the result: | |
| − | * | + | *The coordinate system defined by $\mathbf{\eta_1}$ and $\mathbf{\eta_2}$ is actually in the direction of the principal axes of the original system. |
| − | * | + | *With $\sigma_1 = \sigma_2$ almost always results $($exception: $\rho= 0)$ the angle of rotation $\alpha = 45^\circ$. |
| − | * | + | *This also follows from the equation given in the theory section: |
:$$\alpha = {1}/{2}\cdot \arctan (2 \cdot\rho \cdot | :$$\alpha = {1}/{2}\cdot \arctan (2 \cdot\rho \cdot | ||
\frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2})= | \frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2})= | ||
{1}/{2}\cdot \arctan | {1}/{2}\cdot \arctan | ||
| − | (\infty)\hspace{0.3cm}\ | + | (\infty)\hspace{0.3cm}\rightarrow\hspace{0.3cm}\alpha = 45^\circ.$$ |
| − | * | + | *The eigenvalues $\lambda_1$ and $\lambda_2$ do not denote the scatter with respect to the new axes, but the variances. |
| − | + | Thus, correct are <u>the proposed solutions 1 and 2</u>. | |
| − | '''(5)''' | + | '''(5)''' By comparing the matrices $\mathbf{K_x}$ and $\mathbf{K_z}$ we get. |
*$\sigma_{1}\hspace{0.15cm}\underline{ =2}$, | *$\sigma_{1}\hspace{0.15cm}\underline{ =2}$, | ||
*$\sigma_{2}\hspace{0.15cm}\underline{ =1}$, | *$\sigma_{2}\hspace{0.15cm}\underline{ =1}$, | ||
| Line 184: | Line 184: | ||
| − | '''(6)''' | + | '''(6)''' According to the now familiar scheme: |
:$$(4- \lambda) \cdot (1- \lambda) -4 = 0\hspace{0.3cm}\Rightarrow | :$$(4- \lambda) \cdot (1- \lambda) -4 = 0\hspace{0.3cm}\Rightarrow | ||
| − | \hspace{0.3cm}\lambda^2 - 5\lambda | + | \hspace{0.3cm}\lambda^2 - 5\lambda = |
0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\hspace{0.15cm}\underline{\lambda_{1} | 0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\hspace{0.15cm}\underline{\lambda_{1} | ||
=5,\hspace{0.1cm} \lambda_{2} =0}.$$ | =5,\hspace{0.1cm} \lambda_{2} =0}.$$ | ||
| Line 192: | Line 192: | ||
| − | '''(7)''' | + | '''(7)''' According to the equation given on the specification sheet: |
:$$\alpha ={1}/{2}\cdot \arctan (2 \cdot 1 \cdot \frac{2 \cdot | :$$\alpha ={1}/{2}\cdot \arctan (2 \cdot 1 \cdot \frac{2 \cdot | ||
1}{2^2 -1^2})= {1}/{2}\cdot \arctan ({4}/{3}) = | 1}{2^2 -1^2})= {1}/{2}\cdot \arctan ({4}/{3}) = | ||
26.56^\circ.$$ | 26.56^\circ.$$ | ||
| − | [[File:P_ID677__Sto_A_4_16_g.png|right|frame| | + | [[File:P_ID677__Sto_A_4_16_g.png|right|frame|Best possible decorrelation]] |
| − | + | The same result is obtained using the eigenvector: | |
:$$\left[ \begin{array}{cc} | :$$\left[ \begin{array}{cc} | ||
4-5 & 2 \\ | 4-5 & 2 \\ | ||
| Line 212: | Line 212: | ||
({\zeta_{12}}/{\zeta_{11}}) = \arctan(0.5) \hspace{0.15cm}\underline{= 26.56^\circ}.$$ | ({\zeta_{12}}/{\zeta_{11}}) = \arctan(0.5) \hspace{0.15cm}\underline{= 26.56^\circ}.$$ | ||
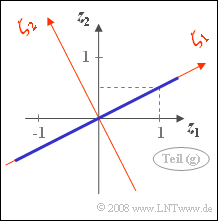
| − | + | The accompanying sketch shows the joint PDF of the random variable $\mathbf{z}$: | |
| − | * | + | *Because $\rho = 1$ all values lie on the correlation line with coordinates $z_1$ and $z_2 = z_1/2$. |
| − | * | + | *By rotating by the angle $\alpha = \arctan(0.5) = 26.56^\circ$ a new coordinate system is formed. |
| − | * | + | *The variance along the axis $\mathbf{\zeta_1}$ is $\lambda_1 = 5$ $($scatter $\sigma_1 = \sqrt{5} = 2.236)$, |
| − | * | + | *while in the direction orthogonal to it $\mathbf{\zeta_2}$ the random variable is not extended $(\lambda_2 = \sigma_2 = 0)$. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 12:29, 15 March 2022
Although the description of Gaussian random variables using vectors and matrices is actually only necessary and makes sense for more than $N = 2$ dimensions, here we restrict ourselves to the special case of two-dimensional random variables for simplicity.
In the graph above, the general correlation matrix $\mathbf{K_x}$ of the 2D–random variable $\mathbf{x} = (x_1, x_2)^{\rm T}$ is given, where $\sigma_1^2$ and $\sigma_2^2$ describe the variances of the individual components. $\rho$ denotes the correlation coefficient between the two components.
The random variables $\mathbf{y}$ and $\mathbf{z}$ give two special cases of $\mathbf{x}$ whose process parameters are to be determined from the correlation matrices $\mathbf{K_y}$ and $\mathbf{K_z}$ respectively.
Hints:
- The exercise belongs to the chapter Generalization to N-Dimensional Random Variables.
- Some basics on the application of vectors and matrices can be found on the pages Determinant of a Matrix and Inverse of a Matrix .
- According to the page Contour lines for correlated random variables the angle $\alpha$ between the old and the new system is given by the following equation:
- $$\alpha = {1}/{2}\cdot \arctan (2 \cdot\rho \cdot \frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2}).$$
- In particular, note:
- A $2×2$-covariance matrix has two real eigenvalues $\lambda_1$ and $\lambda_2$.
- These two eigenvalues determine two eigenvectors $\xi_1$ and $\xi_2$.
- These span a new coordinate system in the direction of the principal axes of the old system.
Questions
Solution
- $\mathbf{K_y}$ is indeed the most general correlation matrix of a 2D random variable with $\sigma_1 = \sigma_2 = \sigma$.
- The parameter $\rho$ specifies the correlation coefficient. This can take all values between $\pm 1$ including these marginal values.
(2) In this case, the governing equation is:
- $${\rm det}\left[ \begin{array}{cc} 1- \lambda & 0 \ 0 & 1- \lambda \end{array} \right] = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} (1- \lambda)^2 = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm} \hspace{0.15cm}\underline{\lambda_{1/2} =1}.$$
(3) With positive $\rho$ the governing equation of the eigenvalues is:
- $$(1- \lambda)^2 -\rho^2 = 0\hspace{0.5cm}\Rightarrow \hspace{0.5cm}\lambda^2 - 2\lambda + 1 - \rho^2 = 0\hspace{0.5cm}\Rightarrow\hspace{0.5cm}\lambda_{1/2} =1 \pm \rho.$$
- For $\rho= 0.5$ one gets $\underline{\lambda_{1} =1.5}$ and $\underline{\lambda_{2} =0.5}$.
- By the way, the equation holds in the whole domain of definition $-1 \le \rho \le +1$.
- For $\rho = 0$ is $\lambda_1 = \lambda_2 = +1$ ⇒ see subtask (2)'.
- For $\rho = \pm 1$ this gives $\lambda_1 = 2$ and $\lambda_2 = 0$.
(4) The eigenvectors are obtained by substituting the eigenvalues $\lambda_1$ and $\lambda_2$ into the correlation matrix:
- $$\left[ \begin{array}{cc} 1- (1+\rho) & \rho \\ \rho & 1- (1+\rho) \end{array} \right]\cdot{\boldsymbol{\eta_1}} = \left[ \begin{array}{cc} -\rho & \rho \\ \rho & -\rho \end{array} \right]\cdot \left[ \begin{array}{c} \eta_{11} \\ \eta_{12} \end{array} \right]=0$$
- $$\Rightarrow\hspace{0.3cm}-\rho \cdot \eta_{11} + \rho \cdot \eta_{12} = 0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\eta_{11}= {\rm const} \cdot \eta_{12}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\boldsymbol{\eta_1}}= {\rm const}\cdot \left[ \begin{array}{c} 1 \\ 1 \end{array} \right];$$
- $$\left[ \begin{array}{cc} 1- (1-\rho) & \rho \\ \rho & 1- (1-\rho) \end{array} \right]\cdot{\boldsymbol{\eta_2}} = \left[ \begin{array}{cc} \rho & \rho \\ \rho & \rho \end{array} \right]\cdot \left[ \begin{array}{c} \eta_{21} \\ \eta_{22} \end{array} \right]=0$$
- $$\Rightarrow\hspace{0.3cm}\rho \cdot \eta_{21} + \rho \cdot \eta_{22} = 0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\eta_{21}= -{\rm const} \cdot \eta_{22}\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\boldsymbol{\eta_2}}= {\rm const}\cdot \left[ \begin{array}{c} -1 \\ 1 \end{array} \right].$$
Putting this into what is called orthonormal form, the following holds:
- $${\boldsymbol{\eta_1}}= \frac{1}{\sqrt{2}}\cdot \left[ \begin{array}{c} 1 \\ 1 \end{array} \right],\hspace{0.5cm} {\boldsymbol{\eta_2}}= \frac{1}{\sqrt{2}}\cdot \left[ \begin{array}{c} -1 \\ 1 \end{array} \right].$$
The sketch illustrates the result:
- The coordinate system defined by $\mathbf{\eta_1}$ and $\mathbf{\eta_2}$ is actually in the direction of the principal axes of the original system.
- With $\sigma_1 = \sigma_2$ almost always results $($exception: $\rho= 0)$ the angle of rotation $\alpha = 45^\circ$.
- This also follows from the equation given in the theory section:
- $$\alpha = {1}/{2}\cdot \arctan (2 \cdot\rho \cdot \frac{\sigma_1\cdot\sigma_2}{\sigma_1^2 -\sigma_2^2})= {1}/{2}\cdot \arctan (\infty)\hspace{0.3cm}\rightarrow\hspace{0.3cm}\alpha = 45^\circ.$$
- The eigenvalues $\lambda_1$ and $\lambda_2$ do not denote the scatter with respect to the new axes, but the variances.
Thus, correct are the proposed solutions 1 and 2.
(5) By comparing the matrices $\mathbf{K_x}$ and $\mathbf{K_z}$ we get.
- $\sigma_{1}\hspace{0.15cm}\underline{ =2}$,
- $\sigma_{2}\hspace{0.15cm}\underline{ =1}$,
- $\rho = 2/(\sigma_{1} \cdot \sigma_{2})\hspace{0.15cm}\underline{ =1}$.
(6) According to the now familiar scheme:
- $$(4- \lambda) \cdot (1- \lambda) -4 = 0\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\lambda^2 - 5\lambda = 0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\hspace{0.15cm}\underline{\lambda_{1} =5,\hspace{0.1cm} \lambda_{2} =0}.$$
(7) According to the equation given on the specification sheet:
- $$\alpha ={1}/{2}\cdot \arctan (2 \cdot 1 \cdot \frac{2 \cdot 1}{2^2 -1^2})= {1}/{2}\cdot \arctan ({4}/{3}) = 26.56^\circ.$$
The same result is obtained using the eigenvector:
- $$\left[ \begin{array}{cc} 4-5 & 2 \\ 2 & 1-5 \end{array} \right]\cdot \left[ \begin{array}{c} \zeta_{11} \\ \zeta_{12} \end{array} \right]=0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}-\zeta_{11}= 2\zeta_{12}=0\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\zeta_{12}={\zeta_{11}}/{2}$$
- $$\Rightarrow\hspace{0.3cm}\alpha = \arctan ({\zeta_{12}}/{\zeta_{11}}) = \arctan(0.5) \hspace{0.15cm}\underline{= 26.56^\circ}.$$
The accompanying sketch shows the joint PDF of the random variable $\mathbf{z}$:
- Because $\rho = 1$ all values lie on the correlation line with coordinates $z_1$ and $z_2 = z_1/2$.
- By rotating by the angle $\alpha = \arctan(0.5) = 26.56^\circ$ a new coordinate system is formed.
- The variance along the axis $\mathbf{\zeta_1}$ is $\lambda_1 = 5$ $($scatter $\sigma_1 = \sqrt{5} = 2.236)$,
- while in the direction orthogonal to it $\mathbf{\zeta_2}$ the random variable is not extended $(\lambda_2 = \sigma_2 = 0)$.