Difference between revisions of "Aufgaben:Exercise 3.2Z: Bessel Spectrum"
From LNTwww
m |
m (→Questions) |
||
| Line 40: | Line 40: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {What are the properties of the signal $x(t)$? |
|type="[]"} | |type="[]"} | ||
| − | - $x(t)$ | + | - $x(t)$ is imaginary for all times $t$ . |
| − | + $x(t)$ | + | + $x(t)$ is periodic. |
| − | - | + | - The spectral function $X(f)$ is obtained via the Fourier integral. |
| − | { | + | {Write the Fourier coefficients $D_n$ together with the Bessel functions of the first kind ⇒ ${\rm J}_n(η)$. What relationships can be seen? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - All $D_n$ are equal to ${\rm J}_η(0)$. |
| − | + | + | + $D_n = {\rm J}_n(η)$ holds. |
| − | - | + | - $D_n = -{\rm J}_η(n)$ holds. |
| − | { | + | { What are the properties of the Fourier coefficients? |
|type="()"} | |type="()"} | ||
| − | + | + | + All $D_n$ are purely real. |
| − | - Alle $D_n$ | + | - Alle $D_n$ are purely imaginary. |
| − | { | + | {For $η = 2$ , the coefficients are $D_0 = 0.224$ and $D_1 = 0.577$. From this, calculate the coefficients $D_2$ and $D_3$. |
|type="{}"} | |type="{}"} | ||
$D_2 \ = \ $ { 0.353 3% } | $D_2 \ = \ $ { 0.353 3% } | ||
$D_3 \ = \ $ { 0.129 3% } | $D_3 \ = \ $ { 0.129 3% } | ||
| − | { | + | {What are the Fourier coefficients $D_{-2}$ and $D_{-3}$ ? |
|type="{}"} | |type="{}"} | ||
$D_{-2} \ = \ $ { 0.353 3% } | $D_{-2} \ = \ $ { 0.353 3% } | ||
Revision as of 15:58, 14 March 2022
Consider the complex signal
- $$x(t) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t) }\hspace{0.05cm}.$$
For example, the equivalent low-pass signal at the output of an angle modulator (PM, FM) can be represented in this form if appropriate normalizations are made.
- When $T_0 = 2π/ω_0$, the Fourier series representation is:
- $$x(t) = \sum_{n = - \infty}^{+\infty}D_n \cdot{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t }\hspace{0.05cm},$$
- $$ D_n = \frac{1}{T_0}\cdot \int_{- T_0/2}^{+T_0/2}x(t) \cdot{\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- These complex Fourier coefficients can be expressed using $n$–th order Bessel functions of the first kind:
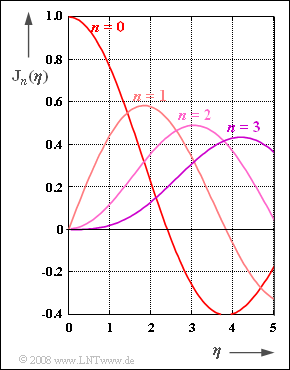
- $${\rm J}_n (\eta) = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha)}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$
- These are shown on the graph in the range $0 ≤ η ≤ 5$ . For negative values of $n$ one obtains:
- $${\rm J}_{-n} (\eta) = (-1)^n \cdot {\rm J}_{n} (\eta)\hspace{0.05cm}.$$
- The series representation of the Bessel functions is:
- $${\rm J}_n (\eta) = \sum\limits_{k=0}^{\infty}\frac{(-1)^k \cdot (\eta/2)^{n \hspace{0.05cm} + \hspace{0.05cm} 2 \hspace{0.02cm}\cdot \hspace{0.05cm}k}}{k! \cdot (n+k)!} \hspace{0.05cm}.$$
- If the function values for $n = 0$ and $n = 1$ are known, the Bessel functions for $n ≥ 2$ can be determined from them by iteration:
- $${\rm J}_n (\eta) = \frac{2 \cdot (n-1)}{\eta} \cdot {\rm J}_{n-1} (\eta) - {\rm J}_{n-2} (\eta) \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter Phase Modulation.
- Particular reference is made to the page Equivalent low-pass signal in phase modulation.
- The values of the Bessel functions can be found in collections of formulae in table form.
- You can also use the interactive applet Bessel functions of the first kind to solve this task.
Questions
Musterlösung
(1) Richtig ist nur der zweite Lösungsvorschlag:
- $x(t)$ ist ein komplexes Signal, das nur in Ausnahmefällen reell wird, zum Beispiel zur Zeit $t = 0$.
- Ein rein imaginärer Wert (zu gewissen Zeiten) kann sich nur dann ergeben, wenn $η ≥ π/2$ ist ⇒ Antwort 1 ist falsch.
- Mit $T_0 = 2π/ω_0$ gilt beispielsweise:
- $$ x(t + k \cdot T_0) = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} (t \hspace{0.05cm}+ \hspace{0.05cm} k \hspace{0.05cm}\cdot \hspace{0.05cm}T_0)) } = {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm} + \hspace{0.05cm} k \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi) } ={\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm}\cdot \hspace{0.05cm} t \hspace{0.05cm} ) } = x(t)\hspace{0.05cm}.$$
- Dieses Signal ist periodisch. Zur Berechnung der Spektralfunktion muss die Fourierreihe und nicht das Fourierintegral herangezogen werden.
(2) Die Fourierkoeffizienten lauten:
- $$ D_n = \frac{1}{T_0}\cdot \int_{- T_0/2}^{+T_0/2}{\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin (\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t) }\cdot{\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n \hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm 0} \hspace{0.05cm} \cdot \hspace{0.05cm} t }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- Durch Zusammenfassen der beiden Terme und nach der Substitution $α = ω_0 · t$ erhält man:
- $$D_n = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {{\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}(\eta \hspace{0.05cm}\cdot \hspace{0.05cm}\sin(\alpha) -\hspace{0.05cm} n \hspace{0.05cm}\cdot \hspace{0.05cm}\alpha)}}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm} = {\rm J}_n (\eta) .$$
- Richtig ist also der zweite Lösungsvorschlag.
(3) Mit dem Satz von Euler können die Fourierkoeffizienten wie folgt dargestellt werden:
- $$D_n = \frac{1}{2\pi}\cdot \int_{-\pi}^{+\pi} {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha + \frac{\rm j}{2\pi}\cdot \int_{-\pi}^{+\pi} {\sin( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$
- Der Integrand des ersten Integrals ist eine gerade Funktion von $\alpha$:
- $$I_1 (-\alpha) = {\cos( \eta \cdot \sin(-\alpha) + n \cdot \alpha)} = {\cos( -\eta \cdot \sin(\alpha) + n \cdot \alpha)}= {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)} = I_1 (\alpha) \hspace{0.05cm}.$$
- Dagegen ist der zweite Integrand eine ungerade Funktion:
- $$I_2 (-\alpha) = {\sin( \eta \cdot \sin(-\alpha) + n \cdot \alpha)} = {\sin( -\eta \cdot \sin(\alpha) + n \cdot \alpha)}= -{\sin( \eta \cdot \sin(\alpha) - n \cdot \alpha)} = -I_2 (\alpha) \hspace{0.05cm}.$$
- Somit verschwindet das zweite Integral und man erhält unter Berücksichtigung der Symmetrie:
- $$D_n = \frac{1}{\pi}\cdot \int_{0}^{\pi} {\cos( \eta \cdot \sin(\alpha) - n \cdot \alpha)}\hspace{0.1cm}{\rm d}\alpha \hspace{0.05cm}.$$
- Richtig ist somit der Lösungsvorschlag 1.
(4) Entsprechend der iterativen Berechnungsformel gilt für $η = 2$:
- $$ D_2 = D_1 - D_0 = 0.577 - 0.224 \hspace{0.15cm}\underline {= 0.353} \hspace{0.05cm},$$
- $$D_3 = 2 \cdot D_2 - D_1 = 2 \cdot 0.353 - 0.577 \hspace{0.15cm}\underline {= 0.129} \hspace{0.05cm}.$$
(5) Aufgrund der angegebenen Symmetriebeziehung gilt weiter:
- $$ D_{–2} = D_2\hspace{0.15cm}\underline {= 0.353} \hspace{0.05cm},$$
- $$D_{–3} = -D_3 \hspace{0.15cm}\underline {= -0.129} \hspace{0.05cm}.$$