Aufgaben:Exercise 3.8: Modulation Index and Bandwidth

• Return to book

Bessel function values

A harmonic oscillation of the form

$$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t + \phi_{\rm N})$$

is angle-modulated and then the one-sided magnitude spectrum  $|S_+(f)|$  is obtained.

• with a message frequency of  $f_{\rm N} = 2 \ \rm kHz$  the following spectral lines can be seen with the following weights:

$$|S_{\rm +}(98\,{\rm kHz})| = |S_{\rm +}(102\,{\rm kHz})| = 1.560\,{\rm V}\hspace{0.05cm},$$ $$|S_{\rm +}(96\,{\rm kHz})| = |S_{\rm +}(104\,{\rm kHz})| = 1.293\,{\rm V}\hspace{0.05cm},$$

$$|S_{\rm +}(94\,{\rm kHz})| = |S_{\rm +}(106\,{\rm kHz})| = 0.594\,{\rm V}\hspace{0.05cm}.$$

Further spectral lines follow each with frequency spacing  $f_{\rm N} = 2 \ \rm kHz$, but are not given here and can be ignored.

• If one increases the message frequency to  $f_{\rm N} = 4 \ \rm kHz$, there occur dominant lines

$$|S_{\rm +}(100\,{\rm kHz})| = 2.013\,{\rm V}\hspace{0.05cm},$$

$$|S_{\rm +}(96\,{\rm kHz})|\hspace{0.2cm} = |S_{\rm +}(104\,{\rm kHz})| = 1.494\,{\rm V}\hspace{0.05cm},$$

$$|S_{\rm +}(92\,{\rm kHz})|\hspace{0.2cm} = |S_{\rm +}(108\,{\rm kHz})| = 0.477\,{\rm V},$$

as well as further, negligible Dirac lines with spacing  $f_{\rm N} = 4 \ \rm kHz$.

Hints:

• This exercise belongs to the chapter  Frequency Modulation.
• Reference is also made to the chapter  Phase Modulation  and particularly to the section  Signal characteristics with frequency modulation.

Questions

1

Which modulation method is used here?

	Phase modulation.
	Frequency modulation.

2

What is the modulation index  $η_2$  at message frequency  $f_{\rm N} = 2 \ \rm kHz$?

$η_2 \ = \ $

3

What is the carrier amplitude?

$A_{\rm T} \ = \ $ $\ \rm V$

4

Specify the bandwidth  $B_2$ for  $f_{\rm N} = 2 \ \rm kHz$  if a distortion factor  $K < 1\%$  is desired.

$B_2 \ = \ $ $\ \rm kHz$

5

What is the modulation index $η_4$  at message frequency  $f_{\rm N} = 4 \ \rm kHz$?

$η_4\ = \ $

6

What channel bandwidth  $B_4$  is now required to ensure  $K < 1\%$ ?

$B_4 \ = \ $ $\ \rm kHz$

Solution

Solution

(1)  Es handelt sich um eine Frequenzmodulation   ⇒   Antwort 2.

• Bei Phasenmodulation würden sich die Gewichte der Diraclinien bei der Frequenzverdopplung nicht ändern.

(2)  Die angegebene Spektralfunktion lässt aufgrund von Symmetrieeigenschaften auf die Trägerfrequenz  $f_{\rm T} = 100 \ \rm kHz$  schließen.

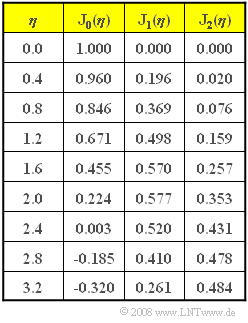
• Da bei  $f_{\rm N} = 2 \ \rm kHz$  die Spektrallinie bei  $f_{\rm T} = 100 \ \rm kHz$  verschwindet, ist  $η_2 \hspace{0.15cm}\underline { ≈ 2.4}$  zu vermuten.
• Eine Kontrolle der weiteren Impulsgewichte bestätigt das Ergebnis:

$$\frac { |S_{\rm +}(f =102\,{\rm kHz})|}{ |S_{\rm +}(f =104\,{\rm kHz})|} = 1.206,\hspace{0.2cm} \frac { {\rm J}_1(2.4)}{ {\rm J}_2(2.4)}= 1.206 \hspace{0.05cm}.$$

(3)  Die Gewichte der Diraclinien bei  $f_{\rm T} + n · f_{\rm N}$  lauten allgemein:

$$D_n = A_{\rm T} \cdot { {\rm J}_n(\eta)} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} D_1 = A_{\rm T} \cdot { {\rm J}_1(\eta)}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} A_{\rm T} = D_1/{\rm J}_1(η) = 1.560\ \rm V/0.520\hspace{0.15cm}\underline { = 3 \ V}.$$

(4)  Mit der Forderung  $K < 1\%$  gilt folgende Faustformel  (Carson–Regel):

$$B_{\rm 2} = 2 \cdot f_{\rm N} \cdot (\eta +2) \hspace{0.15cm}\underline {= 17.6\,{\rm kHz}}\hspace{0.05cm}.$$

• Somit stehen dem Empfänger die Fourierkoeffizienten  $D_{–4}$, ... , $D_4$  zur Verfügung.

(5)  Bei Frequenzmodulation gilt allgemein:

$$\eta = \frac{K_{\rm FM} \cdot A_{\rm N}}{ \omega_{\rm N}} \hspace{0.05cm}.$$

• Durch Verdopplung der Nachrichtenfrequenz $f_{\rm N}$ wird also der Modulationsindex halbiert:   $η_4 = η_2/2\hspace{0.15cm}\underline { = 1.2}$.

(6)  Die für  $K < 1\%$  erforderliche Kanalbandbreite ergibt sich nach gleicher Rechnung wie in der Teilaufgabe  (4)  zu

$$B_4 = 3.2 · 8\ \rm kHz \hspace{0.15cm}\underline {= 25.6 \ \rm kHz}.$$

• Aufgrund des nur halb so großen Modulationsindex' genügt es für die Begrenzung des Klirrfaktors auf  $1\%$, die Fourierkoeffizienten  $D_{–3}$, ... , $D_3$  zu übertragen.