Aufgaben:Exercise 3.10: Noise Power Calculation

• Return to book

Rauschleistungsdichten von PM und FM

Consider the phase and frequency modulation of a cosine oscillation with frequency   $f_{\rm N}$.  . First, let the message frequency be  $f_{\rm N} = f_5 = 5 \ \rm kHz$  and the modulation index (phase deviation) be  $η = 5$.

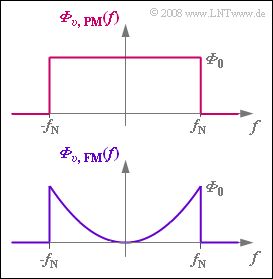
In the presence of additive Gaussian noise with noise power density  $N_0$ , the PM demodulator results in a constant noise power density  ${\it \Phi}_{v {\rm , \hspace{0.08cm}PM} }(f) = {\it \Phi}_0$, which also depends on the modulation index  $η$ :

$${\it \Phi}_0 = \frac{N_0}{\eta^2} \hspace{0.05cm}.$$

For the calculation of the noise power  $P_{\rm R}$ , only the frequency range  $±f_{\rm N}$  is relevant (see graph).

The noise power density after FM demodulation with the frequency deviation  $Δf_{\rm A}$ is:

$${\it \Phi}_{v {\rm , \hspace{0.08cm}FM} } (f) = N_0 \cdot \left(\frac{f}{\Delta f_{\rm A}}\right)^2 \hspace{0.05cm}.$$

• The signal-to-noise ratio  $10 · \lg ρ_v = 50 \ \rm dB$  is given for phase modulation with  $f_{\rm N} = 5 \ \rm kHz$.
• In this task, we are looking for the S/N ratio of FM for the message frequency  $f_{\rm N} = 5 \ \rm kHz$  as well as the resulting S/N ratios of PM and FM for message frequency  $f_{\rm N} = f_{10} = 10 \ \rm kHz$.

Hints:

• This exercise belongs to the chapter  Influence of Noise on Systems with Angle Modulation.
• Particular reference is made to the section  System comparison of AM, PM and FM with respect to noise.

Questions

1

Welcher Rauschabstand ergibt sich bei  Phasenmodulation  und  $f_{\rm N} = 10 \ \rm kHz$?  Interpretieren Sie das Ergebnis.

$10 · \lg ρ_v \ = \ $ $\ \rm dB$

2

Berechnen Sie den Rauschabstand bei  Frequenzmodulation  und  $f_{\rm N} = 5 \ \rm kHz$.  Wie groß ist der Modulationsindex bei dieser Konstellation?

$10 · \lg ρ_v \ = \ $ $\ \rm dB$

3

Berechnen Sie den Rauschabstand bei  Frequenzmodulation  und  $f_{\rm N} = 10 \ \rm kHz$.  Interpretieren Sie das Ergebnis im Vergleich zu  (1)  und  (2).

$10 · \lg ρ_v \ = \ $ $\ \rm dB$

Musterlösung

Solution

(1)  Das Signal–zu–Rausch–Leistungsverhältnis  (Sinken–SNR)  $ \rho_{v }$  ist der Quotient aus Nutzleistung  $P_{\rm S}$  und Rauschleistung  $P_{\rm R}$.  Für die Phasenmodulation gilt:

$$ \rho_{v } = \frac{P_{\rm S}}{P_{\rm R}} = \frac{P_{\rm S}}{{\it \Phi}_0 \cdot 2 f_{\rm N} } =\frac{\eta^2}{2} \cdot \frac{P_{\rm S}}{N_0 \cdot f_{\rm N} }\hspace{0.05cm}.$$

• Die Messung mit  $f_{\rm N} = f_5 = 5 \ \rm kHz$  hat das SNR  $ \rho_{v } = 10^5$  $($entsprechend  $10 · \lg ρ_v =50\ \rm dB)$  ergeben.
• Die doppelte Nachrichtenfrequenz führt zum halben SNR, da nun die doppelte Rauschleistung wirksam ist:

$$ \rho_{v }= 0.5 \cdot 10^5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}\underline {\approx 46.99\,{\rm dB}}\hspace{0.05cm}.$$

Dieses Ergebnis lässt sich auch über die Beziehung  $ρ_v = η^2/2 · ξ$  herleiten.

• Bei Phasenmodulation ist  $η$  unabhängig von der Nachrichtenfrequenz.
• Der SNR–Verlust geht darauf zurück, dass nun die Leistungskenngröße  $ξ = P_{\rm S}/(N_0 · f_{\rm N})$  halbiert wird.

(2)  Bei Frequenzmodulation und der Nachrichtenfrequenz  $f_{\rm N} = 5 \ \rm kHz$  erhält man für die Rauschleistung:

$$P_{\rm R} = \int_{-f_{\rm N}}^{ + f_{\rm N}} {\it \Phi}_{v {\rm , \hspace{0.08cm}FM} } (f)\hspace{0.1cm}{\rm d}f = \frac{2 \cdot N_0}{\Delta f_{\rm A}^{\hspace{0.1cm}2}} \cdot \int_{0}^{ f_{\rm N}} f^2\hspace{0.1cm}{\rm d}f = \frac{2 \cdot N_0 \cdot f_{\rm N}^{\hspace{0.1cm}3}}{3 \cdot \Delta f_{\rm A}^2} \hspace{0.05cm}.$$

• Unter Berücksichtigung des Frequenzhubs  $Δf_{\rm A} = η · f_{\rm N}$  ergibt sich somit:

$$P_{\rm R} = \frac{2 \cdot N_0 \cdot f_{\rm N}}{3 \cdot \eta^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v }= \frac{3 \cdot \eta^2 \cdot P_{\rm S}}{2 \cdot N_0 \cdot f_{\rm N}} = 3 \cdot \rho_{v {\rm , \hspace{0.08cm}PM}}\hspace{0.05cm}.$$

• Das heißt:  Die Frequenzmodulation ist um den Faktor  $3$  $($oder $4.77 \ \rm dB)$  besser als die Phasenmodulation:

$$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }= 50\,{\rm dB} + 10 \cdot {\rm lg} \hspace{0.15cm}{3}\hspace{0.15cm}\underline {\approx 54.77\,{\rm dB}}\hspace{0.05cm}.$$

(3)  Entsprechend dem Ergebnis der Teilaufgabe  (2)  erhält man mit  $f_{10} = 10 \ \rm kHz$:

$$P_{\rm R} = \frac{2 \cdot N_0 \cdot f_{\rm 10}}{3 \cdot \eta_{10}^{\hspace{0.1cm}2}} = \frac{ f_{\rm 10} \cdot \eta_{5}^{\hspace{0.1cm}2}}{ 3 \cdot f_{\rm 5} \cdot \eta_{10}^{\hspace{0.1cm}2}}\cdot \frac{2 \cdot N_0 \cdot f_{\rm 5}}{\eta_{5}^{\hspace{0.1cm}2}} \hspace{0.05cm}.$$

• Der zweite Term gibt die Rauschleistung des Vergleichssystems  $($PM, $f_{\rm N} = f_5)$  an,  die zum Ergebnis  $10 · \lg ρ_v = 50\ \rm dB$  geführt hat.

• Bei Frequenzmodulation ist nun jedoch der Modulationsindex  $η$  umgekehrt proportional zur Nachrichtenfrequenz, so dass der Quotient  $η_5^2/η_{10}^2 = 4$  ist.
• Somit ergibt sich für den Vorfaktor  $8/3$.  Aufgrund der größeren Rauschleistung ist das SNR kleiner:

$$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }= 50\,{\rm dB} - 10 \cdot {\rm lg} \hspace{0.15cm}({8}/{3})\hspace{0.15cm}\underline {\approx 45.74\,{\rm dB}}\hspace{0.05cm}.$$

Bei gleicher Nachrichtenfrequenz  $f_{\rm N} = 10 \ \rm kHz$  ist nun die FM um  $1.25 \ \rm dB$  schlechter als die PM, da sich nun die Halbierung von  $η$  – nach Quadrierung der Faktor  $4$  –  stärker auswirkt als der systembedingte Faktor  $3$, um den die FM gegenüber der PM überlegen ist.

• Der Vergleich der Teilaufgaben  (2)  und  (3)  zeigt einen Unterschied um den Faktor  $8$  bzw.  $9.03 \ \rm dB$.
• Der ungünstigere Wert für die größere Nachrichtenfrequenz  $f_{\rm N} = 10 \ \rm kHz$  ergibt sich durch den nur halb so großen Modulationsindex – nach Quadrierung Faktor  $4$  – und die doppelte Rauschbandbreite.