Difference between revisions of "Aufgaben:Exercise 1.10Z: Gaussian Band-Pass"
| Line 3: | Line 3: | ||
}} | }} | ||
| − | [[File:P_ID1697__Dig_Z_4_3.png|right|frame|Gaussian | + | [[File:P_ID1697__Dig_Z_4_3.png|right|frame|Gaussian band-pass channel]] |
For this exercise we assume: | For this exercise we assume: | ||
| − | *Binary phase modulation (BPSK) is used for modulation. | + | *Binary phase modulation $\rm (BPSK)$ is used for modulation. |
| − | *Demodulation is frequency and phase | + | *Demodulation is synchronous in frequency and phase. |
| − | For carrier frequency modulated transmission, the channel frequency response $H_{\rm K}(f)$ must always be assumed to be a | + | For carrier frequency modulated transmission, the channel frequency response $H_{\rm K}(f)$ must always be assumed to be a band-pass. The channel parameters are e.g. the center frequency $f_{\rm M}$ and the bandwidth $\Delta f_{\rm K}$, where the center frequency (German: "Mittenfrequenz" ⇒ subscipt: "M") $f_{\rm M}$ often coincides with the carrier frequency (German: "Trägerfrequenz" ⇒ subscipt: "T") $f_{\rm T}$. |
| − | In this exercise | + | In this exercise we will assume a Gaussian band-pass according to the diagram. For its frequency response holds: |
:$$H_{\rm K}(f) = {\rm exp} \left [ - \pi \cdot \left ( \frac {f - f_{\rm M} }{\Delta f_{\rm K}}\right )^2 \right ] | :$$H_{\rm K}(f) = {\rm exp} \left [ - \pi \cdot \left ( \frac {f - f_{\rm M} }{\Delta f_{\rm K}}\right )^2 \right ] | ||
+{\rm exp} \left [ - \pi \cdot \left ( \frac {f + f_{\rm M} }{\Delta f_{\rm K}}\right )^2 \right ]$$ | +{\rm exp} \left [ - \pi \cdot \left ( \frac {f + f_{\rm M} }{\Delta f_{\rm K}}\right )^2 \right ]$$ | ||
| − | For a simpler description, one often uses the equivalent TP frequency response $H_{\rm K,TP}(f)$. This results from $H_{\rm K}(f)$ by | + | For a simpler description, one often uses the equivalent low-pass ("TP") frequency response $H_{\rm K,TP}(f)$. This results from $H_{\rm K}(f)$ by |
*truncating the components at negative frequencies, | *truncating the components at negative frequencies, | ||
| + | |||
*shifting the spectrum by $f_{\rm T}$ to the left. | *shifting the spectrum by $f_{\rm T}$ to the left. | ||
| − | In the considered example with $f_{\rm T} = f_{\rm M}$ for the equivalent | + | In the considered example with $f_{\rm T} = f_{\rm M}$ for the equivalent low-pass frequency response results: |
:$$ H_{\rm K,\hspace{0.04cm} TP}(f) = {\rm e}^ { - \pi \hspace{0.04cm}\cdot \hspace{0.04cm}\left ( {f }/{\Delta f_{\rm K}}\right )^2 }.$$ | :$$ H_{\rm K,\hspace{0.04cm} TP}(f) = {\rm e}^ { - \pi \hspace{0.04cm}\cdot \hspace{0.04cm}\left ( {f }/{\Delta f_{\rm K}}\right )^2 }.$$ | ||
| − | The corresponding time function (Fourier | + | The corresponding time function ("inverse Fourier transform") is: |
:$$ h_{\rm K,\hspace{0.04cm} TP}(t) = \Delta f_{\rm K} \cdot {\rm e}^ { - \pi \hspace{0.04cm}\cdot \hspace{0.04cm}\left ( {\Delta f_{\rm K}} \cdot t \right )^2 }.$$ | :$$ h_{\rm K,\hspace{0.04cm} TP}(t) = \Delta f_{\rm K} \cdot {\rm e}^ { - \pi \hspace{0.04cm}\cdot \hspace{0.04cm}\left ( {\Delta f_{\rm K}} \cdot t \right )^2 }.$$ | ||
| − | However, the frequency response is also suitable for describing a phase-synchronous BPSK system in the low-pass range | + | However, the frequency response is also suitable for describing a phase-synchronous BPSK system in the low-pass range |
:$$H_{\rm MKD}(f) = {1}/{2} \cdot \left [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\right ] ,$$ | :$$H_{\rm MKD}(f) = {1}/{2} \cdot \left [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\right ] ,$$ | ||
| − | where "MKD" stands for modulator – channel (Kanal) – demodulator. Often - but not always - $H_{\rm MKD}(f)$ and $H_{\rm K,TP}(f)$ are identical. | + | where "MKD" stands for "modulator – channel (Kanal) – demodulator". Often - but not always - $H_{\rm MKD}(f)$ and $H_{\rm K,TP}(f)$ are identical. |
| + | Notes: | ||
| + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation|"Linear Digital Modulation - Coherent Demodulation"]]. | ||
| − | + | *Reference is made in particular to the section [[Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation#Baseband_model_for_ASK_and_BPSK|"Baseband model for ASK and BPSK"]]. | |
| − | |||
| − | *Reference is made in particular to the section [[Digital_Signal_Transmission/Linear_Digital_Modulation_-_Coherent_Demodulation#Baseband_model_for_ASK_and_BPSK|Baseband model for ASK and BPSK]]. | ||
| Line 42: | Line 43: | ||
<quiz display=simple> | <quiz display=simple> | ||
| − | {Give the impulse response $h_{\rm K}(t)$ of the Gaussian | + | {Give the impulse response $h_{\rm K}(t)$ of the Gaussian band-pass channel. What is the (normalized) value for time $t = 0$? |
|type="{}"} | |type="{}"} | ||
$ h_{\rm K}(t)/\Delta f_{\rm K} \ = \ $ { 2 3% } | $ h_{\rm K}(t)/\Delta f_{\rm K} \ = \ $ { 2 3% } | ||
| Line 54: | Line 55: | ||
+The time function $h_{\rm MKD}(t)$ is real. | +The time function $h_{\rm MKD}(t)$ is real. | ||
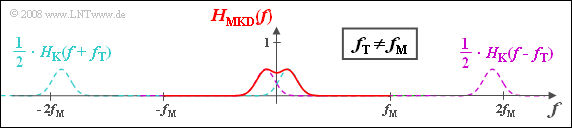
| − | {Which statements are true under the condition $f_{\rm T} \neq f_{\rm M}$? | + | {Which statements are true under the condition $f_{\rm T} \neq f_{\rm M}$? |
|type="[]"} | |type="[]"} | ||
-$H_{\rm K,TP}(f)$ and $H_{\rm MKD}(f)$ coincide completely. | -$H_{\rm K,TP}(f)$ and $H_{\rm MKD}(f)$ coincide completely. | ||
Revision as of 15:00, 7 May 2022
For this exercise we assume:
- Binary phase modulation $\rm (BPSK)$ is used for modulation.
- Demodulation is synchronous in frequency and phase.
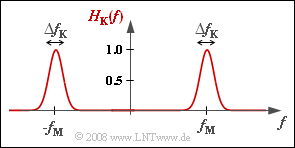
For carrier frequency modulated transmission, the channel frequency response $H_{\rm K}(f)$ must always be assumed to be a band-pass. The channel parameters are e.g. the center frequency $f_{\rm M}$ and the bandwidth $\Delta f_{\rm K}$, where the center frequency (German: "Mittenfrequenz" ⇒ subscipt: "M") $f_{\rm M}$ often coincides with the carrier frequency (German: "Trägerfrequenz" ⇒ subscipt: "T") $f_{\rm T}$.
In this exercise we will assume a Gaussian band-pass according to the diagram. For its frequency response holds:
- $$H_{\rm K}(f) = {\rm exp} \left [ - \pi \cdot \left ( \frac {f - f_{\rm M} }{\Delta f_{\rm K}}\right )^2 \right ] +{\rm exp} \left [ - \pi \cdot \left ( \frac {f + f_{\rm M} }{\Delta f_{\rm K}}\right )^2 \right ]$$
For a simpler description, one often uses the equivalent low-pass ("TP") frequency response $H_{\rm K,TP}(f)$. This results from $H_{\rm K}(f)$ by
- truncating the components at negative frequencies,
- shifting the spectrum by $f_{\rm T}$ to the left.
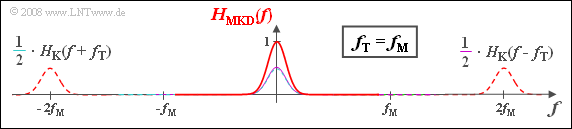
In the considered example with $f_{\rm T} = f_{\rm M}$ for the equivalent low-pass frequency response results:
- $$ H_{\rm K,\hspace{0.04cm} TP}(f) = {\rm e}^ { - \pi \hspace{0.04cm}\cdot \hspace{0.04cm}\left ( {f }/{\Delta f_{\rm K}}\right )^2 }.$$
The corresponding time function ("inverse Fourier transform") is:
- $$ h_{\rm K,\hspace{0.04cm} TP}(t) = \Delta f_{\rm K} \cdot {\rm e}^ { - \pi \hspace{0.04cm}\cdot \hspace{0.04cm}\left ( {\Delta f_{\rm K}} \cdot t \right )^2 }.$$
However, the frequency response is also suitable for describing a phase-synchronous BPSK system in the low-pass range
- $$H_{\rm MKD}(f) = {1}/{2} \cdot \left [ H_{\rm K}(f-f_{\rm T}) + H_{\rm K}(f+f_{\rm T})\right ] ,$$
where "MKD" stands for "modulator – channel (Kanal) – demodulator". Often - but not always - $H_{\rm MKD}(f)$ and $H_{\rm K,TP}(f)$ are identical.
Notes:
- The exercise belongs to the chapter "Linear Digital Modulation - Coherent Demodulation".
- Reference is made in particular to the section "Baseband model for ASK and BPSK".
Questions
Solution
- $$H_{\rm K}(f) = H_{\rm K,\hspace{0.04cm} TP}(f) \star \big [ \delta (f - f_{\rm M}) + \delta (f + f_{\rm M}) \big ] .$$
- The Fourier inverse transform of the bracket expression yields a cosine function of frequency $f_{\rm M}$ with amplitude $2$.
- Thus, according to the convolution theorem:
- $$h_{\rm K}(t) = 2 \cdot \Delta f_{\rm K} \cdot {\rm exp} \left [ - \pi \cdot \left ( {\Delta f_{\rm K}} \cdot t \right )^2 \right ] \cdot \cos(2 \pi f_{\rm M} t ) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}h_{\rm K}(t = 0)/\Delta f_{\rm K} \hspace{0.1cm}\underline {= 2}.$$
- This means: The TP impulse response $h_{\rm K,\hspace{0.04cm}TP}(t)$ is identical in shape to the envelope of the bp impulse response $h_{\rm K}(t)$, but twice as large.
(2) Statements 2, 3 and 4 are correct:
- The first statement is false because $H_{\rm MKD}(f)$ also has components around $\pm 2f_{\rm T}$.
- The time function $h_{\rm K,\hspace{0.04cm}TP}(t)$ is real according to the given equation.
- The same is true for $h_{\rm MKD}(t)$ also considering the $\pm 2f_{\rm T}$ components, since $H_{\rm MKD}(f)$ is an even function with respect to $f = 0$.
- The diagram shows $H_{\rm MKD}(f)$, which also has components around $\pm 2f_{\rm T}$. At low frequencies, $H_{\rm K,\hspace{0.04cm}TP}(f)$ is identical to $H_{\rm MKD}(f)$.
(3) Only solution 4 is correct:
- Here $H_{\rm K,\hspace{0.04cm}TP}(f)$ and $H_{\rm MKD}(f)$ differ even at the low frequencies.
- $H_{\rm K,\hspace{0.04cm}TP}(f)$ is a Gaussian function with the maximum at $f_{ε} = f_{\rm M} - f_{\rm T}$.
- Because of this asymmetry, $h_{\rm K,\hspace{0.04cm}TP}(t)$ is complex.
- In contrast, $H_{\rm MKD}(f)$ is still an even function with respect to $f = 0$ with real impulse response $h_{\rm MKD}(t)$.
- $H_{\rm MKD}(f)$ is composed of two Gaussian functions at $± f_ε$.
(4) Correct is of course the first answer.