Linear and Time Invariant Systems/Linear Distortions: Difference between revisions
From LNTwww
Die Seite wurde neu angelegt: „ {{Header |Untermenü=Signalverzerrungen und Entzerrung |Vorherige Seite=Nichtlineare Verzerrungen |Nächste Seite=Folgerungen aus dem Zuordnungssatz }} ==Zus…“ |
No edit summary |
||
| Line 7: | Line 7: | ||
==Zusammenstellung wichtiger Beschreibungsgrößen== | ==Zusammenstellung wichtiger Beschreibungsgrößen== | ||
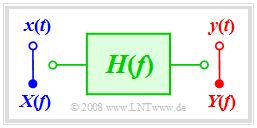
Für diesen Abschnitt 2.3 werden nichtlineare Verzerrungen ausgeschlossen, so dass das System durch den Frequenzgang $H(f)$ vollständig beschrieben wird: | Für diesen Abschnitt 2.3 werden nichtlineare Verzerrungen ausgeschlossen, so dass das System durch den Frequenzgang $H(f)$ vollständig beschrieben wird: | ||
[[File:P_ID899__LZI_T_2_3_S1_neu.png |400px | Beschreibung eines linearen Systems]] | |||
Der im Allgemeinen komplexe Frequenzgang kann auch wie folgt dargestellt werden: | |||
$$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot | |||
\hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} | |||
\hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$ | |||
Daraus ergeben sich folgende Beschreibungsgrößen: | |||
*Der Betrag $|H(f)|$ wird als Amplitudengang und in logarithmierter Form als Dämpfungsverlauf bezeichnet: | |||
$$a(f) = - \ln |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Neper | |||
\hspace{0.1cm}(Np) } = - 20 \cdot \lg |H(f)|\hspace{0.2cm}{\rm in | |||
\hspace{0.1cm}Dezibel \hspace{0.1cm}(dB) }.$$ | |||
*Der Phasengang $b(f)$ gibt den negativen frequenzabhängigen Winkel von $H(f)$ in der komplexen Ebene an, bezogen auf die reelle Achse: | |||
$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in | |||
\hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$ | |||
Revision as of 16:01, 5 May 2016
Zusammenstellung wichtiger Beschreibungsgrößen
Für diesen Abschnitt 2.3 werden nichtlineare Verzerrungen ausgeschlossen, so dass das System durch den Frequenzgang $H(f)$ vollständig beschrieben wird:
Der im Allgemeinen komplexe Frequenzgang kann auch wie folgt dargestellt werden: $$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$
Daraus ergeben sich folgende Beschreibungsgrößen:
- Der Betrag $|H(f)|$ wird als Amplitudengang und in logarithmierter Form als Dämpfungsverlauf bezeichnet:
$$a(f) = - \ln |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Neper \hspace{0.1cm}(Np) } = - 20 \cdot \lg |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Dezibel \hspace{0.1cm}(dB) }.$$
- Der Phasengang $b(f)$ gibt den negativen frequenzabhängigen Winkel von $H(f)$ in der komplexen Ebene an, bezogen auf die reelle Achse:
$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in \hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$
