Difference between revisions of "Aufgaben:Exercise 1.08: Comparison of ASK and BPSK"
| Line 62: | Line 62: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' It is already obvious from the equations on the information page that <u>solution 2</u> is correct. The defining equations are: | + | '''(1)''' It is already obvious from the equations on the information page that <u>solution 2</u> is correct. The defining equations are: |
:$$\rm Q ({\it x}) = \ \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it | :$$\rm Q ({\it x}) = \ \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it | ||
x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u | x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u | ||
| Line 69: | Line 69: | ||
\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u | \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | By simple substitutions, the above relationship can be easily proved: | + | *By simple substitutions, the above relationship can be easily proved: |
:$${\rm Q} ( x) = 1/2 \cdot {\rm erfc} (x/\sqrt{2}) \hspace{0.05cm}.$$ | :$${\rm Q} ( x) = 1/2 \cdot {\rm erfc} (x/\sqrt{2}) \hspace{0.05cm}.$$ | ||
| − | '''(2)''' The <u>first two solutions</u> are correct: | + | '''(2)''' The <u>first two solutions</u> are correct: |
| − | *The equations are valid only for the AWGN channel and for an optimal binary receiver, for example, according to the matched filter approach. | + | *The equations are valid only for the AWGN channel and for an optimal binary receiver, for example, according to the matched filter approach. |
| − | *Intersymbol interfering – caused by the channel or the receiver filter – is not covered by this. | + | *Intersymbol interfering – caused by the channel or the receiver filter – is not covered by this. |
| − | *The exact transmission pulse shaping, on the other hand, does not matter as long as the receiver filter $H_{\rm E}(f)$ is matched to the transmission spectrum. Rather: | + | *The exact transmission pulse shaping, on the other hand, does not matter as long as the receiver filter $H_{\rm E}(f)$ is matched to the transmission spectrum. Rather: |
| − | *Two different transmission pulse shapers $H_{\rm S}(f)$ lead to exactly the same error probability if they have the same energy per bit. | + | *Two different transmission pulse shapers $H_{\rm S}(f)$ lead to exactly the same error probability if they have the same energy per bit. |
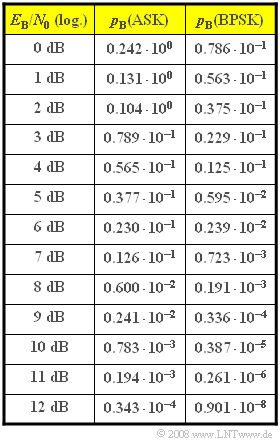
'''(3)''' The results can be read directly from the table: | '''(3)''' The results can be read directly from the table: | ||
| − | :$$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.343 \cdot 10^{-4}}, | + | :$$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.343 \cdot 10^{-4}},$$ |
| + | :$$p_{\rm BPSK} \hspace{0.1cm}\underline {= 0.901 \cdot 10^{-8}}.$$ | ||
'''(4)''' With $E_{\rm B}/N_{0} = 8\ \Rightarrow \ 10 \cdot \lg \ E_{\rm B}/N_{0} \approx 9 \ \rm dB$, the following error probabilities are obtained: | '''(4)''' With $E_{\rm B}/N_{0} = 8\ \Rightarrow \ 10 \cdot \lg \ E_{\rm B}/N_{0} \approx 9 \ \rm dB$, the following error probabilities are obtained: | ||
| − | :$$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.241 \cdot 10^{-2}} | + | :$$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.241 \cdot 10^{-2}}$$ |
| + | :$$p_{\rm BPSK} \hspace{0.1cm}\underline {= 0.336 \cdot 10^{-4}}.$$ | ||
| − | '''(5)''' From question '''(3)''', it follows that for binary phase modulation, $10 \cdot \lg \ E_{\rm B}/N_{0} \approx 12 \ \rm dB$ must be satisfied for $p_{\rm BPSK} \approx 10^{-8}$ to be possible. | + | '''(5)''' From question '''(3)''', it follows that for binary phase modulation, $10 \cdot \lg \ E_{\rm B}/N_{0} \approx 12 \ \rm dB$ must be satisfied for $p_{\rm BPSK} \approx 10^{-8}$ to be possible. |
| − | *However, the given equations also show that the ASK curve is $3 \ \rm dB$ $($exactly $3.01 \ \rm dB)$ to the right of the BPSK curve. | + | *However, the given equations also show that the ASK curve is $3 \ \rm dB$ $($exactly $3.01 \ \rm dB)$ to the right of the BPSK curve. |
*It follows that: | *It follows that: | ||
:$$10 \cdot {\rm lg}\hspace{0.1cm}(E_{\rm B}/N_{\rm 0})_{\rm min}\hspace{0.1cm}\underline {\approx 15\,\,{\rm dB}} \hspace{0.05cm}.$$ | :$$10 \cdot {\rm lg}\hspace{0.1cm}(E_{\rm B}/N_{\rm 0})_{\rm min}\hspace{0.1cm}\underline {\approx 15\,\,{\rm dB}} \hspace{0.05cm}.$$ | ||
Latest revision as of 14:12, 6 May 2022
The bit error probabilities of "Amplitude Shift Keying" $\rm (ASK)$ and "Binary Shift Keying" $\rm (BPSK)$ modulation are often given by the following two equations:
- $$p_{\rm ASK} = \ {\rm Q}\left ( \sqrt{\frac{E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{2 \cdot N_0 }} \right ),$$
- $$ p_{\rm BPSK} = \ {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = \ {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{ N_0 }} \right ).$$
These equations are evaluated in the attached table. The following applies:
- $E_{\rm B}$ indicates the average energy per bit.
- $N_{0}$ is the noise power density.
- There is a fixed relationship between the error functions ${\rm Q}(x)$ and ${\rm erfc}(x)$.
It should be noted that these equations do not apply in general, but only under certain idealized conditions. These conditions are to be worked out in this exercise.
Notes:
- The exercise belongs to the chapter "Linear Digital Modulation - Coherent Demodulation".
- You can check the results with the HTML5/JavaScript applet "Complementary Gaussian Error Functions".
Questions
Solution
- $$\rm Q ({\it x}) = \ \frac{\rm 1}{\sqrt{\rm 2\pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u \hspace{0.05cm},$$
- $$\rm erfc ({\it x}) = \ \frac{\rm 2}{\sqrt{\rm \pi}}\int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}}\,d \it u \hspace{0.05cm}.$$
- By simple substitutions, the above relationship can be easily proved:
- $${\rm Q} ( x) = 1/2 \cdot {\rm erfc} (x/\sqrt{2}) \hspace{0.05cm}.$$
(2) The first two solutions are correct:
- The equations are valid only for the AWGN channel and for an optimal binary receiver, for example, according to the matched filter approach.
- Intersymbol interfering – caused by the channel or the receiver filter – is not covered by this.
- The exact transmission pulse shaping, on the other hand, does not matter as long as the receiver filter $H_{\rm E}(f)$ is matched to the transmission spectrum. Rather:
- Two different transmission pulse shapers $H_{\rm S}(f)$ lead to exactly the same error probability if they have the same energy per bit.
(3) The results can be read directly from the table:
- $$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.343 \cdot 10^{-4}},$$
- $$p_{\rm BPSK} \hspace{0.1cm}\underline {= 0.901 \cdot 10^{-8}}.$$
(4) With $E_{\rm B}/N_{0} = 8\ \Rightarrow \ 10 \cdot \lg \ E_{\rm B}/N_{0} \approx 9 \ \rm dB$, the following error probabilities are obtained:
- $$p_{\rm ASK} \hspace{0.1cm}\underline {= 0.241 \cdot 10^{-2}}$$
- $$p_{\rm BPSK} \hspace{0.1cm}\underline {= 0.336 \cdot 10^{-4}}.$$
(5) From question (3), it follows that for binary phase modulation, $10 \cdot \lg \ E_{\rm B}/N_{0} \approx 12 \ \rm dB$ must be satisfied for $p_{\rm BPSK} \approx 10^{-8}$ to be possible.
- However, the given equations also show that the ASK curve is $3 \ \rm dB$ $($exactly $3.01 \ \rm dB)$ to the right of the BPSK curve.
- It follows that:
- $$10 \cdot {\rm lg}\hspace{0.1cm}(E_{\rm B}/N_{\rm 0})_{\rm min}\hspace{0.1cm}\underline {\approx 15\,\,{\rm dB}} \hspace{0.05cm}.$$