Aufgaben:Exercise 2.7: AMI Code

• Return to book

Block diagram of a pseudo ternary encoder

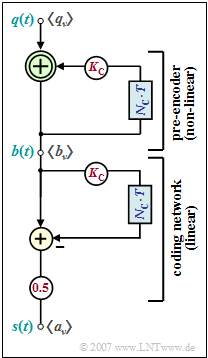
The diagram shows the block diagram for AMI coding, assuming binary bipolar amplitude coefficients  $q_{\nu} ∈ \{–1, +1\}$  at the input. This recoding is done in two stages:

• In the first part of the block diagram, a binary precoded symbol  $b_{\nu}$  is generated at each clock step from the modulo-2 addition of  $q_{\nu}$  and  $b_{\nu -1}$.  It holds  $b_{\nu} ∈ \{–1, +1\}.$
• Then, the current amplitude coefficient of the ternary transmitted signal  $s(t)$  is determined by a conventional subtraction. Thereby holds:

$$a_\nu = {1}/{2} \cdot \left [ b_\nu - b_{\nu-1} \right ] \hspace{0.05cm}.$$

Due to AMI coding, it is ensured that no long "$+1$"– or "$–1$" sequences are created. Modified AMI codes have also been developed to avoid long zero sequences:

• In the HDB3 code, four consecutive zeros each are marked by a specific violation of the AMI coding rule.
• In the B6ZS code, six consecutive zeros are marked by a targeted violation of the AMI coding rule.

The power-spectral density  ${\it \Phi}_{a}(f)$  of the amplitude coefficients is to be obtained from the discrete ACF values  $\varphi_{a}(\lambda) = {\E}\big[a_{\nu} \cdot a_{\nu + \lambda}\big]$.  The Fourier transform in discrete representation is:

$${\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} \hspace{0.05cm}.$$

Notes:

• The exercise belongs to the chapter  "Symbol-Wise Coding with Pseudo Ternary Codes".

• You can check the results with the interactive applet  "Signals, ACF and PSD of pseudo ternary codes". 

Questions

1

At the input,  $\langle q_{\nu} \rangle = \langle +1, –1, +1, +1, –1, +1, +1, –1, –1, –1, –1, +1 \rangle$  is applied. Determine the binary precoded sequence  $\langle b_{\nu} \rangle$  with the default $b_{0} = \hspace{0.05cm}–1$.
Enter the following values as a check:

$b_{1} \hspace{0.26cm} = \ $

$b_{11} \ = \ $

$b_{12} \ = \ $

2

Furthermore, determine the sequence  $\langle a_{\nu} \rangle$  of the amplitude coefficients of the AMI-coded transmitted signal  $s(t)$.
Enter the following values to check the results:

$a_{1} \hspace{0.28cm} = \ $

$a_{11} \ = \ $

$a_{12} \ = \ $

3

Would an HDB3 or a B6ZS signal differ from the AMI code in the range under consideration  $(\text{i.e. above }12T)$? 

	The HDB3 code is different from the AMI code.
	The B6ZS code is different from the AMI code.

4

What are the three probabilities of occurrence in the AMI code?

${\Pr}(a_{\nu} = + 1) \ = \ $

${\Pr}(a_{\nu} = 0) \hspace{0.45cm} = \ $

${\Pr}(a_{\nu} = - 1) \ = \ $

5

Calculate the first two mean values of the amplitude coefficients.

$\E\big[a_{\nu}\big] \ = \ $

$\E\big[a_{\nu}^{2}\big] \ = \ $

6

Calculate the auto-correlation function  $\varphi_{a}(\lambda)$, in particular the following ACF values:

$\varphi_{a}(\lambda = 0) \ = \ $

$\varphi_{a}(\lambda = 1) \ = \ $

$\varphi_{a}(\lambda = 2) \ = \ $

7

What is the power-spectral density  ${\it \Phi}_{a}(f)$? What are the values for  $f = 0$  and  $f = 1/(2T)$?

${\it \Phi}_{a}(f = 0) \ = \ $

${\it \Phi}_{a}(f = 1/(2T)) \ = \ $

Solution

Solution

(1)  The modulo-2 addition can also be taken as an antivalence.

• It is $b_{\nu} = +1$ if $q_{\nu}$ and $b_{\nu – 1}$ differ, otherwise set $b_{\nu} = -1$.
• With the initial value $b_{0} = -1$ we obtain:

$$b_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} b_2 = +1, \hspace{0.2cm}b_3 = -1, \hspace{0.2cm}b_4 = +1, \hspace{0.2cm}b_5 = +1, \hspace{0.2cm}b_6 = -1\hspace{0.05cm},$$

$$b_7 = +1, \hspace{0.2cm} b_8 = +1, \hspace{0.2cm}b_9 = +1, \hspace{0.2cm}b_{10} = +1, \hspace{0.2cm}b_{11} \hspace{0.15cm}\underline {= +1}, \hspace{0.2cm}b_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$

(2)  AMI coding gives the following amplitude coefficients:

$$a_1\hspace{0.15cm}\underline { = +1}, \hspace{0.2cm} a_2 = 0, \hspace{0.2cm}a_3 = -1, \hspace{0.2cm}a_4 = +1, \hspace{0.2cm}a_5 = 0, \hspace{0.2cm}a_6 = -1\hspace{0.05cm},$$

$$a_7 = +1, \hspace{0.2cm} a_8 = 0, \hspace{0.2cm}a_9 = 0, \hspace{0.2cm}a_{10} = 0, \hspace{0.2cm}a_{11}\hspace{0.15cm}\underline { = 0}, \hspace{0.2cm}a_{12} \hspace{0.15cm}\underline {= -1}\hspace{0.05cm}.$$

This result is obtained by the equation $a_{\nu} = (b_{\nu} - b_{\nu –1})/2$ or by direct application of the AMI coding rule:

• A source symbol $q_{\nu} = -1$ always leads to $a_{\nu} = 0$.
• Source symbols $q_{\nu} = +1$ lead alternately to $a_{\nu} = +1$ and $a_{\nu} = -1$.

(3)  Solution 1 is correct:

• The AMI code yields four consecutive zeros in the range between $\nu = 8$ and $\nu = 11$.
• In the HDB3 code, these four symbols would be marked with "$+ 0 0 +$". Thus, the AMI rule is deliberately violated for identification purposes.
• In contrast, the B6ZS code substitutes only zero sequences over six symbols.

(4)  Assuming equally probable binary values $±1$, we obtain ${\Pr}(a_{\nu} = 0) = {\Pr}(q_{\nu} = -1)\hspace{0.15cm}\underline{ = 1/2}$ and for symmetry reasons

${\Pr}(a_{\nu} = +1) = {\Pr}(a_{\nu} = -1) \hspace{0.15cm}\underline{ = 1/4}.$

(5)  Using the probabilities calculated in (4), we obtain:

$${\rm E}\big[a_\nu \big] = \ {1}/{4} \cdot (+1) +{1}/{2} \cdot 0+ {1}/{4} \cdot (-1)\hspace{0.15cm}\underline {= 0}\hspace{0.05cm},$$

$$ {\rm E}\big[a_\nu^2 \big] = \ {1}/{4} \cdot (+1)^2 +{1}/{2} \cdot 0^2 + {1}/{4} \cdot (-1)^2 \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$

(6)  The ACF value at $\lambda = 0$ is equal to the root mean square of the amplitude coefficients:

$$ \varphi_a(\lambda = 0) = {\rm E}[a_\nu^2] \hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$

• Since the order of the AMI code is $N = 1$, for $\lambda > 1$:   $\varphi_a(\lambda > 1) = {\rm E}[a_\nu^2] \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$

• The ACF value $\varphi_{a}(\lambda = 1)$ must be determined by averaging:   $\varphi_a(\lambda = 1) = {\rm E}[a_\nu \cdot a_{\nu+1} \cdot {\rm Pr}(a_\nu \cap a_{\nu+1})] \hspace{0.05cm}.$

• Of the nine possible combinations for $a_{\nu} \cdot a_{\nu +1}$, only four yield a nonzero value. In the other cases, either $a_{\nu} = 0$ or $a_{\nu +1} = 0$.

However, since in AMI code also

$${\rm Pr}[(a_\nu = +1) \cap (a_{\nu+1}= +1)] = \ 0 \hspace{0.05cm},$$

$$ {\rm Pr}[(a_\nu = -1) \cap (a_{\nu+1}= -1)] = \ 0$$

is true,

$${\rm Pr}[(a_\nu = +1) \cap (a_{\nu+1}= -1)] = \ {\rm Pr}(a_\nu = +1)\cdot {\rm Pr}(a_{\nu+1} = -1 | a_\nu = +1) = {1}/{4}\cdot{1}/{2} ={1}/{8} \hspace{0.05cm},$$

$${\rm Pr}[(a_\nu = -1) \cap (a_{\nu+1}= +1)] = \ {\rm Pr}(a_\nu = -1)\cdot {\rm Pr}(a_{\nu+1} = +1 | a_\nu = -1) = {1}/{4}\cdot {1}/{2} = {1}/{8}$$

Auto-correlation functions of the AMI code

is obtained as the final result (since the ACF is always an even function):

$$\varphi_{a}(\lambda = +1) = \varphi_{a}(\lambda = –1) = –0.25.$$

• This takes into account that $a_{\nu} = +1$ is followed by $a_{\nu +1} = +1$ and $a_{\nu +1} = -1$ with equal probability.
• Thus, the result is:

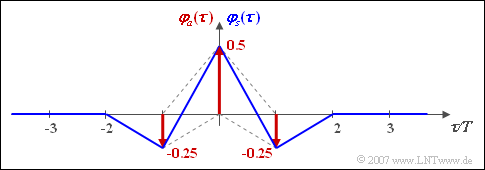
$$\varphi_a(\lambda = 0)\hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}, $$

$$\varphi_a(\lambda = 1)\hspace{0.15cm}\underline {= -0.25} \hspace{0.05cm},$$

$$\varphi_a(\lambda = 2)\hspace{0.15cm}\underline {= 0}.$$

The graph shows

• the discrete ACF $\varphi_{a}(\lambda)$ of the amplitude coefficients and
• the ACF $\varphi_{s}(\tau)$ of the transmitted signal under the condition of NRZ rectangular pulses and AMI coding.

Here, the ACF $\varphi_{s}(\tau)$ drawn in blue is the result of the (discrete) convolution between the discrete ACF $\varphi_{a}(\lambda)$ – drawn in red – and the triangular energy ACF of the basic transmission pulse.

(7)  From the given equation, taking into account the discrete ACF values calculated in (6)

$$\varphi_{a}(\lambda = 0) = 1/2,$$

$$\varphi_{a}(|\lambda| = 1) = -1/4,$$

$$\varphi_{a}(|\lambda| > 1) = 0$$

we obtain the following result:

$${\it \Phi}_a(f) = \ \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda T} = \varphi_a(\lambda = 0) + 2 \cdot \varphi_a(\lambda = 1 )\cdot\cos ( 2 \pi f \hspace{0.02cm} \lambda T) = \ {1}/{2} \cdot \left [ 1 - \cos ( 2 \pi f \hspace{0.02cm} T)\right ] = \sin^2 ( \pi f \hspace{0.02cm} T) \hspace{0.05cm}.$$

In particular, holds:

$${\it \Phi}_a(f = 0) \hspace{0.15cm}\underline {= 0},$$

$${\it \Phi}_a(f = {1}/({2T})) = \sin^2 ({\pi}/{2})\hspace{0.15cm}\underline {= 1} \hspace{0.05cm}.$$