Difference between revisions of "Aufgaben:Exercise 1.2Z: Three-dimensional Representation of Codes"
From LNTwww
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Objective_of_Channel_Coding |
}} | }} | ||
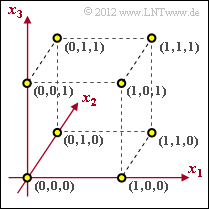
| − | [[File:P_ID2400__KC_Z_1_2.png|right|frame| | + | [[File:P_ID2400__KC_Z_1_2.png|right|frame|Space $\rm GF(2^3)$ and <br>Code of length $n = 3$]] |
| − | Codes | + | Codes for error detection or error correction can be represented very clearly in $n$-dimensional space. We restrict ourselves here to binary codes of length $n = 3$: |
:$$\underline{x} = (x_{1}, x_{2}, x_{3}) \hspace{0.1cm} \in \hspace{0.1cm}{\rm GF}(2^3) \hspace{0.05cm},\hspace{0.5cm} x_i = \{0, 1 \}\hspace{0.05cm},\hspace{0.2cm} i = 1, 2, 3\hspace{0.05cm}.$$ | :$$\underline{x} = (x_{1}, x_{2}, x_{3}) \hspace{0.1cm} \in \hspace{0.1cm}{\rm GF}(2^3) \hspace{0.05cm},\hspace{0.5cm} x_i = \{0, 1 \}\hspace{0.05cm},\hspace{0.2cm} i = 1, 2, 3\hspace{0.05cm}.$$ | ||
| − | + | In general, for block coding: | |
| − | * | + | *The information word $\underline{u} = (u_{1}, u_{2}, \ \text{...} , \ u_{k})$ is uniquely transformed into the codeword $\underline{x} =(x_{1}, x_{2}, \ \text{...} , \ , x_{n})$ . |
| − | * | + | *The code rate is $R = k/n$. |
| − | * | + | *The Hamming distance $d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')$ between two codewords $x ∈ \mathcal{C}$ and $x\hspace{0.05cm}' ∈ \mathcal{C}$ indicates the number of bit positions in which $x$ and $x\hspace{0.05cm}'$ differ. |
| − | * | + | *The minimum distance $d_{\rm min} = {\rm min}\big[d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')\big]$ is a measure of the correctability of a code. |
| − | * | + | *It can $e =d_{\rm min} - 1$ detect errors and $t =(d_{\rm min} - 1)/2$ correct errors. |
| − | * | + | *The last statement, however, is valid only for odd $d_{\rm min}$. |
| Line 19: | Line 19: | ||
| − | + | Hints: | |
| − | * | + | *This exercise belongs to the chapter [[Channel_Coding/Objective_of_Channel_Coding|Obective of Channel Coding]] |
| − | * | + | *In addition, some simple questions about the chapter [[Channel_Coding/Examples_of_Binary_Block_Codes|Examples of binary block codes]] are anticipated. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements hold if all points in $\rm GF(2^3)$ are occupied? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The assignment $\underline{u} = (u_{1}, u_{2}, u_{3})$ → $\underline{x} = (x_{1}, x_{2},x_{3})$ holds. |
| − | - | + | - The identity $\underline{x} = \underline{u}$ holds. |
| − | + | + | + The code rate is $R = 1$. |
| − | - | + | -The minimum distance between two codewords is $d_{\rm min} = 2$. |
| − | { | + | {Which statements are true for a (3, 2, 2)-block code? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + code $\mathcal{C}_{1} = \{(0, 0, 0), (0, 1, 1), (1, 0, 1), (1, 1, 0)\}$ is possible. |
| − | + Code $\mathcal{C}_{2} | + | + Code $\mathcal{C}_{2} = \{(0, 0, 1), (0, 1, 0), (1, 0, 0), (1, 1, 1)\}$ is possible. |
| − | - Code $\mathcal{C}_{3} | + | - Code $\mathcal{C}_{3} = \{(0, 0, 0), (0, 1, 1), (1, 0, 0), (1, 1, 1)\}$ is possible. |
| − | { | + | {What properties does the code defined in subtask '''(2)''' show $\mathcal{C}_{1}$? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + A bit error can be detected. |
| − | - | + | - A bit error can be corrected. |
| − | { | + | {What properties does the code show $\mathcal{C}_{4}= \{(0, 0, 0), (1, 1, 1)\}$? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The code rate is $R = 1/4$. |
| − | + | + | + The code rate is $R = 1/3$. |
| − | + | + | + A bit error can be detected. |
| − | + | + | + A bit error can be corrected. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct <u>statements 1 and 3</u>: |
| − | * | + | *In this assignment, $k = 3$ information bits are mapped to $n = 3$ code bits ⇒ $R = k/n = 1$. |
| − | * | + | *The statement $\underline{x} = \underline{u} $ would only hold in the case of systematic coding. |
| − | * | + | *For example, in principle, $(0, 0, 0)$ → $(0, 1, 1)$ would also be possible. |
| − | * | + | *The last statement is certainly false: from the graph one can see the minimum distance $d_{\rm min} = 1$. |
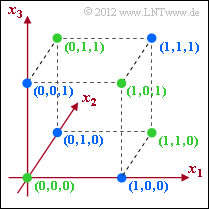
| − | [[File:P_ID2401__KC_Z_1_2b.png|right|frame| | + | [[File:P_ID2401__KC_Z_1_2b.png|right|frame|Two (3, 2, 2)-block codes]] |
| − | '''(2)''' | + | '''(2)''' Correct <u>statements 1 and 3</u>: |
| − | *$\mathcal{C}_{1}$ | + | *$\mathcal{C}_{1}$ and $\mathcal{C}_{2}$ actually describe codes with rate $R = 2/3$ and minimum distance $d_{\rm min} = 2$. |
| − | *In | + | *In the graph, the green dots mark the code $\mathcal{C}_{1}$ and the blue dots mark the code $\mathcal{C}_{2}$. |
| − | * | + | *For the code $\mathcal{C}_{3}$ - also with rate $R = 2/3$ - the minimum distance between two codewords is $d_{\rm min} = 1$, for example between $(0, 0, 0)$ and $(1, 0, 0)$ or between $(0, 1, 1)$ and $(1, 1, 1)$. |
| − | '''(3)''' | + | '''(3)''' Correct is only <u>statement 1</u>: |
| − | * | + | *Only a bit error can be detected with the minimum distance $d_{\rm min} = 2$. |
| − | *In | + | *In the upper graph, the green dots indicate allowed codewords of $\mathcal{C}_{1}$. If a blue dot is received, this indicates a transmission error. |
| − | * | + | *On the other hand, error correction is not possible with $d_{\rm min} = 2$. |
| − | * | + | *The code $\mathcal{C}_{1}$ corresponds to the [[Channel_Coding/Examples_of_Binary_Block_Codes#Single_Parity_Check_Codes|Single Parity-check Code (3, 2, 2)]]. |
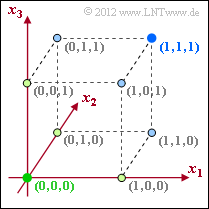
| − | [[File:P_ID2402__KC_Z_1_2d.png|right|frame|(3, 1, 3) | + | [[File:P_ID2402__KC_Z_1_2d.png|right|frame|(3, 1, 3) block code]] |
| − | '''(4)''' | + | '''(4)''' Correct <u>answers 2, 3, and 4</u>: |
| − | *$C_{4}$ | + | *$C_{4}$ describes the [[Channel_Coding/Examples_of_Binary_Block_Codes#Repetition_Codes|(3, 1, 3) repetition code]]. |
| − | * | + | *In this code, two of the total eight possible points are occupied, from which one could incorrectly conclude the code rate $R = 1/4$. However, the code rate is calculated according to $R = k/n = 1/3$. |
| − | * | + | *From the lower diagram one recognizes that because of $d_{\rm min} = 3$ now also a bit error can be corrected. |
| − | * | + | *During decoding, all light green points (with black outline) are transferred to the green point $(0, 0, 0)$ and all light blue points are transferred to the blue point $(1, 1, 1)$. |
| − | * | + | *Up to two bit errors can be detected at the same time (one of course). |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 17:13, 4 June 2022
Codes for error detection or error correction can be represented very clearly in $n$-dimensional space. We restrict ourselves here to binary codes of length $n = 3$:
- $$\underline{x} = (x_{1}, x_{2}, x_{3}) \hspace{0.1cm} \in \hspace{0.1cm}{\rm GF}(2^3) \hspace{0.05cm},\hspace{0.5cm} x_i = \{0, 1 \}\hspace{0.05cm},\hspace{0.2cm} i = 1, 2, 3\hspace{0.05cm}.$$
In general, for block coding:
- The information word $\underline{u} = (u_{1}, u_{2}, \ \text{...} , \ u_{k})$ is uniquely transformed into the codeword $\underline{x} =(x_{1}, x_{2}, \ \text{...} , \ , x_{n})$ .
- The code rate is $R = k/n$.
- The Hamming distance $d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')$ between two codewords $x ∈ \mathcal{C}$ and $x\hspace{0.05cm}' ∈ \mathcal{C}$ indicates the number of bit positions in which $x$ and $x\hspace{0.05cm}'$ differ.
- The minimum distance $d_{\rm min} = {\rm min}\big[d_{\rm H}(x, \hspace{0.05cm}x\hspace{0.05cm}')\big]$ is a measure of the correctability of a code.
- It can $e =d_{\rm min} - 1$ detect errors and $t =(d_{\rm min} - 1)/2$ correct errors.
- The last statement, however, is valid only for odd $d_{\rm min}$.
Hints:
- This exercise belongs to the chapter Obective of Channel Coding
- In addition, some simple questions about the chapter Examples of binary block codes are anticipated.
Questions
Solution
(1) Correct statements 1 and 3:
- In this assignment, $k = 3$ information bits are mapped to $n = 3$ code bits ⇒ $R = k/n = 1$.
- The statement $\underline{x} = \underline{u} $ would only hold in the case of systematic coding.
- For example, in principle, $(0, 0, 0)$ → $(0, 1, 1)$ would also be possible.
- The last statement is certainly false: from the graph one can see the minimum distance $d_{\rm min} = 1$.
(2) Correct statements 1 and 3:
- $\mathcal{C}_{1}$ and $\mathcal{C}_{2}$ actually describe codes with rate $R = 2/3$ and minimum distance $d_{\rm min} = 2$.
- In the graph, the green dots mark the code $\mathcal{C}_{1}$ and the blue dots mark the code $\mathcal{C}_{2}$.
- For the code $\mathcal{C}_{3}$ - also with rate $R = 2/3$ - the minimum distance between two codewords is $d_{\rm min} = 1$, for example between $(0, 0, 0)$ and $(1, 0, 0)$ or between $(0, 1, 1)$ and $(1, 1, 1)$.
(3) Correct is only statement 1:
- Only a bit error can be detected with the minimum distance $d_{\rm min} = 2$.
- In the upper graph, the green dots indicate allowed codewords of $\mathcal{C}_{1}$. If a blue dot is received, this indicates a transmission error.
- On the other hand, error correction is not possible with $d_{\rm min} = 2$.
- The code $\mathcal{C}_{1}$ corresponds to the Single Parity-check Code (3, 2, 2).
(4) Correct answers 2, 3, and 4:
- $C_{4}$ describes the (3, 1, 3) repetition code.
- In this code, two of the total eight possible points are occupied, from which one could incorrectly conclude the code rate $R = 1/4$. However, the code rate is calculated according to $R = k/n = 1/3$.
- From the lower diagram one recognizes that because of $d_{\rm min} = 3$ now also a bit error can be corrected.
- During decoding, all light green points (with black outline) are transferred to the green point $(0, 0, 0)$ and all light blue points are transferred to the blue point $(1, 1, 1)$.
- Up to two bit errors can be detected at the same time (one of course).