Difference between revisions of "Aufgaben:Exercise 1.13: Binary Erasure Channel Decoding"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Decoding_of_Linear_Block_Codes}} |
| − | [[File:KC_A_1_13_neu.png|right|frame| | + | [[File:KC_A_1_13_neu.png|right|frame|Decoding at the BEC]] |
| − | + | We assume here the model in section [[Channel_Coding/Decoding_of_Linear_Block_Codes#Decoding_at_the_Binary_Erasure_Channel|"Decoding at the Binary Erasure Channel"]] (BEC configuration highlighted in green): | |
| − | * | + | *Each information word $\underline{u}$ is encoded blockwise and yields the codeword $\underline{x}$. Let the block code be linear and completely given by its parity-check matrix $\boldsymbol{\rm H}$. |
| − | * | + | *During transmission $n_{\rm E}$ bits of the codeword are erased ⇒ [[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Erasure_Channel_.E2.80.93_BEC|"Binary Erasure Channel"]] (BEC). The codeword $\underline{x}$ thus becomes the received word $\underline{y}$. |
| − | * | + | *If the number $n_{\rm E}$ of erasures is less than the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|"minimum distance"]] $d_{\rm min}$ of the code, it is possible to reconstruct from $\underline{y}$ the codeword $\underline{z} = \underline{x}$ without error, and thus the correct information word $\underline{v} = \underline{u}$ is also obtained. |
| − | + | For exercise description, let us now consider the Hamming codeword $\underline{x} = (0, 1, 0, 1, 1, 0, 0)$ and the received word $\underline{y} = (0, 1, {\rm E} , {\rm E}, 1, 0, 0).$ | |
| − | * | + | *The third and fourth bit were thus erased by the channel. |
| − | * | + | *The codeword finder thus has the exercise to determine the vector $z_{\rm E} = (z_{3}, z_{4})$ with $z_{3}, \ z_{4} \in \{0, 1\}$ to be determined. This is done according to the equation |
:$${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T}\hspace{0.05cm}.$$ | :$${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T}\hspace{0.05cm}.$$ | ||
| − | * | + | *In the present example: |
:$$\underline{z}_{\rm K} = (0, 1, 1, 0, 0)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm K} = \begin{pmatrix} 1 &1 &1 &0 &0\\ 0 &1 &0 &1 &0\\ 1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0\\ 1 &1\\ 0 &1 \end{pmatrix} \hspace{0.05cm}.$$ | :$$\underline{z}_{\rm K} = (0, 1, 1, 0, 0)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm K} = \begin{pmatrix} 1 &1 &1 &0 &0\\ 0 &1 &0 &1 &0\\ 1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0\\ 1 &1\\ 0 &1 \end{pmatrix} \hspace{0.05cm}.$$ | ||
| − | * | + | *This equation gives two equations of determination for the bits to be determined, whose solution leads to the result $z_{3} = 0$ and $z_{4} = 1$ . |
| Line 31: | Line 31: | ||
| − | + | Hints: | |
| − | * | + | * This exercise belongs to the chapter [[Channel_Coding/Decoding_of_Linear_Block_Codes|"Decoding of Linear Block Codes"]]. |
| − | * | + | * The algorithm for mapping the received word $\underline{y}$ to the correct codeword $\underline{z} = \underline{x}$ is described in detail in the [[Channel_Coding/Decoding_of_Linear_Block_Codes#Decoding_at_the_Binary_Erasure_Channel|"Theory section"]] . |
| − | * | + | * We would like to remind again that in BEC decoding we use the first decoder block $\underline{y} → \underline{z}$ as ''codeword finder'' since wrong decisions are excluded here. Each received word is decoded correctly, or it may not be decoded at all. |
| − | * | + | *In the BSC model, on the other hand, decoding errors cannot be avoided. Accordingly, we refer to the corresponding block there as ''code word estimator''. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | { $\underline{y} = (1, {\rm E}, 0, 1, 0, 0, {\rm E})$ was received. Which sequence does the codeword finder decide to use? |
|type="()"} | |type="()"} | ||
- $\underline{z} = (1, 0, 0, 1, 0, 0, 0),$ | - $\underline{z} = (1, 0, 0, 1, 0, 0, 0),$ | ||
| Line 48: | Line 48: | ||
- $\underline{z} = (1, 0, 0, 1, 0, 0, 1).$ | - $\underline{z} = (1, 0, 0, 1, 0, 0, 1).$ | ||
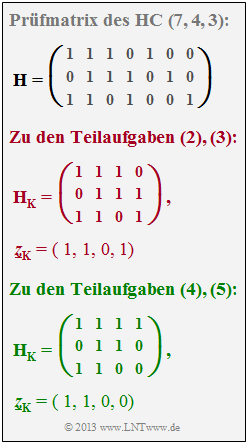
| − | { | + | {What are the consequences of the red entries for $\boldsymbol{\rm H}_{\rm K}$ and $z_{\rm K}$ (see graphic on the information page)? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The erasure vector is $\underline{z}_{\rm E} = (z_{5}, z_{6}, z_{7}).$ |
| − | + | + | + The received word is $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E}).$ |
| − | - $\boldsymbol{\rm H}_{\rm E}$ | + | - $\boldsymbol{\rm H}_{\rm E}$ is a $2 \times 3$ matrix. |
| − | + $\boldsymbol{\rm H}_{\rm E}$ | + | + $\boldsymbol{\rm H}_{\rm E}$ is a $3 \times 3$ matrix. |
| − | { | + | {Now apply $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E}).$ Which codeword is selected? |
|type="()"} | |type="()"} | ||
- $\underline{z} = (1, 1, 0, 1, 1, 1, 0),$ | - $\underline{z} = (1, 1, 0, 1, 1, 1, 0),$ | ||
+ $\underline{z} = (1, 1, 0, 1, 0, 0, 1),$ | + $\underline{z} = (1, 1, 0, 1, 0, 0, 1),$ | ||
- $\underline{z} = (1, 1, 0, 0, 0, 1, 0).$ | - $\underline{z} = (1, 1, 0, 0, 0, 1, 0).$ | ||
| − | - | + | - For the present $\underline{y}$ no unique decoding is possible. |
| − | { | + | {What are the consequences of the green entries for $\boldsymbol{\rm H}_{\rm K}$ and $z_{\rm K}$ (see graphic on the information page)? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The received word is $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E}).$ |
| − | - $\boldsymbol{\rm H}_{\rm K}$ | + | - $\boldsymbol{\rm H}_{\rm K}$ differs from subquestion '''(2)''' in the last row. |
| − | + $\boldsymbol{\rm H}_{\rm K}$ | + | + $\boldsymbol{\rm H}_{\rm K}$ differs from subquestion '''(2)''' in the last column. |
| − | { | + | {Now apply $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E}).$ Which codeword is selected? |
|type="()"} | |type="()"} | ||
- $\underline{z} = (1, 1, 0, 1, 1, 1, 0),$ | - $\underline{z} = (1, 1, 0, 1, 1, 1, 0),$ | ||
- $\underline{z} = (1, 1, 0, 1, 0, 0, 1),$ | - $\underline{z} = (1, 1, 0, 1, 0, 0, 1),$ | ||
- $\underline{z} = (1, 1, 0, 0, 0, 1, 0).$ | - $\underline{z} = (1, 1, 0, 0, 0, 1, 0).$ | ||
| − | + | + | + For the present $\underline{y}$ no unique decoding is possible. |
| − | { | + | {Which statements result for the correction capability at the BEC? $n_{\rm E}$ indicates in the following the number of erasures. |
|type="[]"} | |type="[]"} | ||
| − | + | + | + For $n_{\rm E} < d_{\rm min}$ unique decoding is always possible. |
| − | - | + | - For $n_{\rm E} = d_{\rm min}$ unique decoding is always possible. |
| − | + | + | + For $n_{\rm E} = d_{\rm min}$ sometimes a unique decoding is possible. |
| − | + | + | + For $n_{\rm E} > d_{\rm min}$ unique decoding is never possible. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
'''(1)''' Der Empfangsvektor lautet $\underline{y} = (1, {\rm E}, 0, 1, 0, 0, {\rm E})$. Ausgelöscht wurden also die Codesymbole an den Positionen 2 und 7. | '''(1)''' Der Empfangsvektor lautet $\underline{y} = (1, {\rm E}, 0, 1, 0, 0, {\rm E})$. Ausgelöscht wurden also die Codesymbole an den Positionen 2 und 7. | ||
Revision as of 22:05, 16 July 2022
We assume here the model in section "Decoding at the Binary Erasure Channel" (BEC configuration highlighted in green):
- Each information word $\underline{u}$ is encoded blockwise and yields the codeword $\underline{x}$. Let the block code be linear and completely given by its parity-check matrix $\boldsymbol{\rm H}$.
- During transmission $n_{\rm E}$ bits of the codeword are erased ⇒ "Binary Erasure Channel" (BEC). The codeword $\underline{x}$ thus becomes the received word $\underline{y}$.
- If the number $n_{\rm E}$ of erasures is less than the "minimum distance" $d_{\rm min}$ of the code, it is possible to reconstruct from $\underline{y}$ the codeword $\underline{z} = \underline{x}$ without error, and thus the correct information word $\underline{v} = \underline{u}$ is also obtained.
For exercise description, let us now consider the Hamming codeword $\underline{x} = (0, 1, 0, 1, 1, 0, 0)$ and the received word $\underline{y} = (0, 1, {\rm E} , {\rm E}, 1, 0, 0).$
- The third and fourth bit were thus erased by the channel.
- The codeword finder thus has the exercise to determine the vector $z_{\rm E} = (z_{3}, z_{4})$ with $z_{3}, \ z_{4} \in \{0, 1\}$ to be determined. This is done according to the equation
- $${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T}\hspace{0.05cm}.$$
- In the present example:
- $$\underline{z}_{\rm K} = (0, 1, 1, 0, 0)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm K} = \begin{pmatrix} 1 &1 &1 &0 &0\\ 0 &1 &0 &1 &0\\ 1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0\\ 1 &1\\ 0 &1 \end{pmatrix} \hspace{0.05cm}.$$
- This equation gives two equations of determination for the bits to be determined, whose solution leads to the result $z_{3} = 0$ and $z_{4} = 1$ .
Hints:
- This exercise belongs to the chapter "Decoding of Linear Block Codes".
- The algorithm for mapping the received word $\underline{y}$ to the correct codeword $\underline{z} = \underline{x}$ is described in detail in the "Theory section" .
- We would like to remind again that in BEC decoding we use the first decoder block $\underline{y} → \underline{z}$ as codeword finder since wrong decisions are excluded here. Each received word is decoded correctly, or it may not be decoded at all.
- In the BSC model, on the other hand, decoding errors cannot be avoided. Accordingly, we refer to the corresponding block there as code word estimator.
Questions
Solution
Ausgehend von der vorgegebenen Prüfmatrix
- $${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &0 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &1 &0 &1 &0 &0 &1 \end{pmatrix}$$
des Hammingcodes erhält man für Vektor und Matrix
- hinsichtlich aller korrekt übertragenen Codesymbole (Index $\rm K$), die dem Codewortfinder bekannt sind:
- $$\underline{z}_{\rm K} = (1, 0, 1, 0, 0)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm K} = \begin{pmatrix} 1 &1 &0 &1 &0\\ 0 &1 &1 &0 &1\\ 1 &0 &1 &0 &0 \end{pmatrix} \hspace{0.05cm},$$
- hinsichtlich der beiden ausgelöschten Codesymbole $z_{2}$ und $z_{7}$ (Index $\rm E$), die zu ermitteln sind:
- $$\underline{z}_{\rm E} = (z_2, z_7)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0\\ 1 &0\\ 1 &1 \end{pmatrix} \hspace{0.05cm}.$$
Die Bestimmungsgleichung lautet somit:
- $${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \begin{pmatrix} 1 &0\\ 1 &0\\ 1 &1 \end{pmatrix} \cdot \begin{pmatrix} z_2 \\ z_7 \end{pmatrix} = \begin{pmatrix} 1 &1 &0 &1 &0\\ 0 &1 &1 &0 &1\\ 1 &0 &1 &0 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} \hspace{0.05cm}.$$
Daraus ergeben sich drei Gleichungen für die beiden Unbekannten $z_{2}$ und $z_{7}$:
- $${\rm (a)}\ z_{2} = 1,$$
- $${\rm (b)}\ z_{2} = 1,$$
- $${\rm (c)}\ z_{2} + z_{7} = 0 \ \Rightarrow \ z_{7}= 1.$$
Somit liefert der Codewortfinder $\underline{z} = (1, 1, 0, 1, 0, 0, 1)$ ⇒ Lösungsvorschlag 2.
(2) Betrachtet man die vorgegebene Matrix $\boldsymbol{\rm H}_{\rm K}$, so erkennt man, dass diese mit den ersten vier Spalten der Prüfmatrix $\boldsymbol{\rm H}$ übereinstimmt.
- Die Auslöschungen betreffen also die letzten drei Bit des Empfangswortes ⇒ $\underline{z}_{\rm E} = (z_{5}, z_{6}, z_{7}) ⇒ \underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E})$.
- Die Erasure–Matrix lautet:
- $${ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$
Richtig sind demzufolge die Aussagen 1, 2 und 4.
(3) Man erhält nach einigen Matrizenmultiplikationen:
- $${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} = \begin{pmatrix} 1 &1 &1 &0\\ 0 &1 &1 &1\\ 1 &1 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \hspace{0.05cm},\hspace{1cm} { \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T} = \begin{pmatrix} 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} z_5 \\ z_6 \\ z_7 \end{pmatrix} = \begin{pmatrix} z_5 \\ z_6 \\ z_7 \end{pmatrix} \hspace{0.05cm}.$$
Durch Gleichsetzen folgt $z_{5} = 0, \ z_{6} = 0, \ z_{7} = 1$ ⇒ Lösungsvorschlag 2.
(4) Der Matrizenvergleich zeigt, dass die ersten drei Spalten von $\boldsymbol{\rm H}$ und $\boldsymbol{\rm H}_{\rm K}$ identisch sind.
- Die vierte Spalte von $\boldsymbol{\rm H}_{\rm K}$ ist gleich der fünften Spalte der Prüfmatrix.
- Daraus folgt für den Vektor $z_{\rm E} = (z_{4}, z_{6}, z_{7})$ und weiter für den Empfangsvektor $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E})$ ⇒ Lösungsvorschlag 1 und 3.
(5) Analog zur Teilaufgabe (3) erhält man nun:
- $${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} = \begin{pmatrix} 1 &1 &1 &1\\ 0 &1 &1 &0\\ 1 &1 &0 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \hspace{0.05cm},\hspace{1cm} { \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T} = \begin{pmatrix} 0 &0 &0\\ 1 &1 &0\\ 1 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} z_4 \\ z_6 \\ z_7 \end{pmatrix} = \begin{pmatrix} 0 \\ z_4 + z_6 \\ z_4 + z_7 \end{pmatrix} \hspace{0.05cm}.$$
- Setzt man nun die beiden Spaltenvektoren gleich, so erhält man nur mehr zwei Gleichungen für die drei Unbekannten ⇒ Lösungsvorschlag 4.
- Oder anders ausgedrückt: Ist die Anzahl der Auslöschungen des BEC–Kanals größer als der Rang der Matrix $\boldsymbol{\rm H}_{\rm E}$, so ergibt sich keine eindeutige Lösung des resultierenden Gleichungssystems.
(6) Zur Lösung dieser Aufgabe beziehen wir uns wieder auf den systematischen Hamming–Code $(7, 4, 3)$ entsprechend der angegebenen Prüfgleichung und der angegebenen Codetabelle.
- Die Informationsbit sind schwarz dargestellt und die Prüfbit rot.
- Die minimale Distanz dieses Codes beträgt $d_{\rm min} = 3$.
Weiter nehmen wir an, dass stets das gelb hinterlegte Codewort $\underline{x} = (1, 1, 0, 1, 0, 0, 1)$ gesendet wurde. Dann gilt:
- Ist die Anzahl $n_{\rm E}$ der Auslöschungen kleiner als $d_{\rm min} = 3$, so ist eine Decodierung nach der hier beschriebenen Methode immer möglich ⇒ siehe beispielsweise Teilaufgabe (1) mit $n_{\rm E}= 2$.
- Auch für $n_{\rm E} = d_{\rm min} = 3$ ist manchmal eine Decodierung möglich, wie in der Teilaufgabe (3) gezeigt. In der Codetabelle gibt es nur ein einziges Codewort, das zum Empfangsvektor $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E})$ passen könnte, nämlich das gelb hinterlegte Codewort $\underline{x} = (1, 1, 0, 1, 0, 0, 1)$ .
- Dagegen konnte $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E})$ entsprechend Teilaufgabe (4) nicht decodiert werden. In der Codetabelle erkennt man neben $(1, 1, 0, 1, 0, 0, 1)$ mit $(1, 1, 0, 0, 0, 1, 0)$ ein weiteres Codewort (grün hinterlegt), das durch die $n_{\rm E} = 3$ Auslöschungen bezüglich Bit 4, 6 und 7 zum Empfangswort $\underline{y}$ wird. Dieser Fall, wenn die $n_{\rm E} = d_{\rm min}$ Auslöschungen genau die $d_{\rm min}$ unterschiedlichen Bit zweier Codeworte betreffen, führt zu einer Matrix $\mathbf{H}_{\rm E}$ mit einem Rang kleiner $d_{\rm min}$.
- Ist $\boldsymbol{\rm H}_{\rm E} > d_{\rm min}$, so ist die Anzahl $n - n_{\rm E}$ der nicht ausgelöschten Bit kleiner als die Anzahl $k$ der Informationsbit. In diesem Fall kann das Codewort natürlich nicht decodiert werden.
Das heißt: Zutreffend sind die Aussagen 1, 3 und 4.