Aufgaben:Exercise 2.6: Modified MS43 Code

• Return to book

Code table of the MMS43 code Korrektur

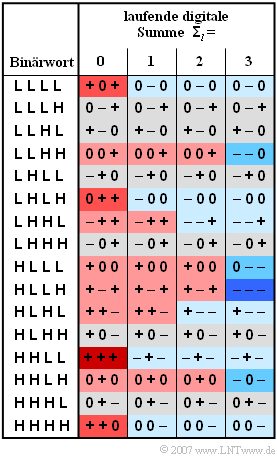
For ISDN data transmission,  the  MMS43 code  ("Modified Monitored Sum 4B3T")  is used in Germany and Belgium on the so-called  $\rm {U_{K0}}$ interface,  which describes the transmission path between the exchange and home.  This is a 4B3T code with four code tables,  which are used for coding according to the running digital sum  (after  $l$ blocks):

$${\it \Sigma}_l = \sum_{\nu = 1}^{3 \hspace{0.02cm}\cdot \hspace{0.05cm} l}\hspace{0.02cm} a_\nu.$$

 ${\it \Sigma}_{0} = 0$  is used for initialization.

The colorings in the table mean:

• If the running digital sum does not change  $({\it \Sigma}_{l+1} = {\it \Sigma}_{l})$,  a field is grayed out.

• An increase  $({\it \Sigma}_{l+1} > {\it \Sigma}_{l})$  is highlighted in red,  a decrease  $({\it \Sigma}_{l+1} < {\it \Sigma}_{l})$  in blue.

• The more intense the coloring,  the larger the change.

Notes:

• The exercise belongs to the chapter  "Block Coding with 4B3T Codes".

• The binary symbols are denoted by  $\rm L$  ("Low")  and  $\rm H$  ("High")  in this learning tutorial.  Often you can find the binary symbols  $\rm L$  and  $\rm 0$  $($instead of  $\rm H)$  in the literature.  Sometimes,  however,  $\rm L$  corresponds to our  $\rm H$  and  $\rm 0$  to   $\rm L$.

• To avoid such confusion and to prevent the  $\rm 0$  from appearing in both alphabets  (binary and ternary)  - in addition with different meanings - we have used the nomenclature which admittedly takes some getting used to.  We are well aware that our nomenclature will also confuse some readers.

• You can check the results with the  (German language)  SWF applet  "Principle of 4B3T coding". 

Questions

1

Why is a 4B3T code used for ISDN instead of the redundancy-free binary code?

	4B3T is always better than the redundancy-free binary code.
	The transmitted signal should be DC signal free because of  $H_{\rm K}(f=0) = 0$.
	A smaller baud rate allows longer cable length.

2

Code the binary sequence  $\rm HHLL\hspace{0.08cm} LHLL\hspace{0.08cm} LHHL\hspace{0.08cm} HLHL$  $($with  ${\it \Sigma}_{0} = 0)$ .
What is the amplitude coefficient of the third ternary symbol of the fourth block?

$a_{12} \ = \ $

3

Determine the Markov diagram for the transition from  ${\it \Sigma}_{l}$  to  ${\it \Sigma}_{l+1}$.  What are the transition probabilities?

$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) \ = \ $

$ {\rm Pr}({\it \Sigma}_{l+1} = 2\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) \ = \ $

$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 2) \ = \ $

4

What properties follow from the Markov diagram?

	Equal probabilities:   ${\rm Pr}({\it \Sigma}_{l} = 0) = \text{...} = {\rm Pr}(\Sigma_{l} = 3)$.
	${\rm Pr}({\it \Sigma}_{l} = 0) = {\rm Pr}({\it \Sigma}_{l} = 3)$   and   ${\rm Pr}({\it \Sigma}_{l} = 1) = {\rm Pr}({\it \Sigma}_{l} = 2)$  are valid.
	The extreme values  $({\it \Sigma}_{l} = 0$  and  ${\it \Sigma}_{l} = 3)$  occur less frequently than the inner values  $({\it \Sigma}_{l} = 1$  and  ${\it \Sigma}_{l} = 2)$.

Solution

Solution

(1)  Statements 2 and 3  are correct:

• The first statement,  on the other hand,  is not true:  For example,  the AWGN ("Additive White Gaussian Noise")  channel with a 4B3T code results in a much larger symbol error probability due to the ternary decision compared to the redundancy-free binary code. 

• The essential reason for the use of a redundant transmission code is rather that no DC signal component can be transmitted via a  "telephone channel".

• The  $25 \%$  smaller baud rate  $(1/T)$  of the 4B3T code compared to the redundancy-free binary code also accommodates the transmission characteristics of symmetrical copper lines  (strong increase in attenuation with frequency). 

• For a given line attenuation,  a greater length can be bridged with the 4B3T code than with a redundancy-free binary signal.

Markov diagram for the MMS43 code

(2)  The 4B3T coding results with the initial value ${\it\Sigma}_{0} = 0$:

• $\rm HHLL$   ⇒   $+ + + \hspace{0.2cm}({\it\Sigma}_{1} = 3)$,
• $\rm LHLL$   ⇒   $– + 0 \hspace{0.2cm}({\it\Sigma}_{2} = 3)$,
• $\rm LHHL$   ⇒   $– – + \hspace{0.2cm}({\it\Sigma}_{3} = 2)$,
• $\rm HLHL$   ⇒   $+ – – \hspace{0.2cm}({\it\Sigma}_{4} = 1)$.

Thus,  the amplitude coefficient we are looking for is  $a_{12} \ \underline{= -\hspace{-0.05cm}1}$.

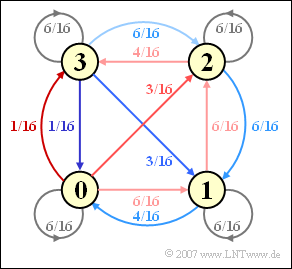
(3)  From the coloring of the code table,  the Markov diagram can be obtained. 

• From it,  one can read the transition probabilities we are looking for:

$$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 6/16 \ \underline{= 0.375},$$

$$ {\rm Pr}({\it \Sigma}_{l+1} = 2\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 0) = 0)= 3/16 \ \underline{= 0.1875},$$

$$ {\rm Pr}({\it \Sigma}_{l+1} = 0\hspace{0.05cm} |\hspace{0.05cm}{\it \Sigma}_{l} = 2) \ \underline{= 0}.$$

(4)  Statements 2 and 3  are correct:

• Statement 1 is false,  recognizable by the asymmetries in the Markov diagram.

• On the other hand,  there are symmetries with respect to the states  "$0$"  and  "$3$"  as well as between  "$1$"  and  "$2$".

• In the following calculation,  instead of  $ {\rm Pr}({\it \Sigma}_{l} = 0)$  we write $ {\rm Pr}(0)$  in a simplified way.

• Taking advantage of the property  ${\Pr}(3) = {\Pr}(0)$  and  ${\Pr}(2) = {\Pr}(1)$,  we obtain from the Markov diagram:

$${\rm Pr}(0)= {6}/{16} \cdot {\rm Pr}(0) +{4}/{16} \cdot {\rm Pr}(1)+ {1}/{16} \cdot {\rm Pr}(3)\hspace{0.15cm} \Rightarrow \hspace{0.15cm}{9}/{16} \cdot {\rm Pr}(0)= {4}/{16} \cdot {\rm Pr}(1)$$

• From the further condition  ${\Pr}(0) + {\Pr}(1) = 1/2$  it follows further:

$${\rm Pr}(0)= {\rm Pr}(3)= {9}/{26}\hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(1)= {\rm Pr}(2)= {4}/{26}\hspace{0.05cm}.$$

This calculation is based on the  "sum of incoming arrows in state  $0$".

One could also give equations for the other three states,  but they all give the same result:

$${\rm Pr}(1) = \ {6}/{16} \cdot {\rm Pr}(0) + {6}/{16} \cdot {\rm Pr}(1)+ {6}/{16} \cdot {\rm Pr}(2)+{3}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$

$$ {\rm Pr}(2) = \ {3}/{16} \cdot {\rm Pr}(0) +{6}/{16} \cdot {\rm Pr}(1)+{6}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm},$$

$${\rm Pr}(3) = \ {1}/{16} \cdot {\rm Pr}(0) + {4}/{16} \cdot {\rm Pr}(2)+{6}/{16} \cdot {\rm Pr}(3)\hspace{0.05cm}.$$