Difference between revisions of "Aufgaben:Exercise 3.7: Optimal Nyquist Equalization once again"
| Line 41: | Line 41: | ||
| − | '' | + | ''Notes:'' |
| − | * | + | *The exercise belongs to the chapter [[Digital_Signal_Transmission/Linear_Nyquist_Equalization|"Linear Nyquist Equalization"]]. |
| − | * | + | * To determine the error probability you can use the interactive calculation module [[Applets:Komplementäre_Gaußsche_Fehlerfunktionen|"Complementary Gaussian Error Functions"]]. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate the magnitude of the transmitter channel frequency response for the frequencies $f = 0$, $f = 1/(2T)= f_{\rm Nyq}$ and $f = 1/T = 2 \cdot f_{\rm Nyq}$. |
|type="{}"} | |type="{}"} | ||
$|H_{\rm SK} (f = 0)| \hspace{0.8cm} = \ $ { 1 3% } | $|H_{\rm SK} (f = 0)| \hspace{0.8cm} = \ $ { 1 3% } | ||
| Line 56: | Line 56: | ||
$|H_{\rm SK} (f = 1/T)| \hspace{0.25cm} = \ $ { 0. } | $|H_{\rm SK} (f = 1/T)| \hspace{0.25cm} = \ $ { 0. } | ||
| − | { | + | {Calculate the maximum value of $H_{\rm TF}(f)$ at frequency $f = f_{\rm Nyq}$. |
|type="{}"} | |type="{}"} | ||
$|H_{\rm TF} (f = f_{\rm Nyq})| \hspace{0.2cm} = \ $ { 1.21 3% } $\ \cdot 10^8$ | $|H_{\rm TF} (f = f_{\rm Nyq})| \hspace{0.2cm} = \ $ { 1.21 3% } $\ \cdot 10^8$ | ||
| − | { | + | {Calculate the normalized noise power according to the triangular approximation. |
|type="{}"} | |type="{}"} | ||
$\sigma_{d, \ \rm norm}^2 \hspace{0.2cm} = \ $ { 1.7 3% } $\ \cdot 10^7$ | $\sigma_{d, \ \rm norm}^2 \hspace{0.2cm} = \ $ { 1.7 3% } $\ \cdot 10^7$ | ||
| − | { | + | {What is the symbol error probability with $s_0^2 \cdot T/N_0 = 10^8$? |
|type="{}"} | |type="{}"} | ||
$p_{\rm S} \hspace{0.2cm} = \ $ { 0.8 3% } $\ \%$ | $p_{\rm S} \hspace{0.2cm} = \ $ { 0.8 3% } $\ \%$ | ||
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' In general, for all frequencies $f \ge 0$: |
:$$|H_{\rm SK}(f)|= {\rm sinc}(f T) \cdot {\rm e}^{ -9.2 | :$$|H_{\rm SK}(f)|= {\rm sinc}(f T) \cdot {\rm e}^{ -9.2 | ||
\cdot \sqrt{2 \cdot |f| \cdot T} }\hspace{0.05cm}.$$ | \cdot \sqrt{2 \cdot |f| \cdot T} }\hspace{0.05cm}.$$ | ||
| − | * | + | *This gives the special cases we are looking for: |
:$$f= 0 \text{:} \ \hspace{0.1cm}|H_{\rm SK}(f = 0)|= {\rm sinc}(0) \cdot {\rm e}^0 \hspace{0.15cm}\underline {= 1} | :$$f= 0 \text{:} \ \hspace{0.1cm}|H_{\rm SK}(f = 0)|= {\rm sinc}(0) \cdot {\rm e}^0 \hspace{0.15cm}\underline {= 1} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| Line 84: | Line 84: | ||
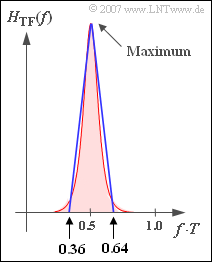
| − | '''(2)''' | + | '''(2)''' The graph shows that $H_{\rm TF}(f)$ becomes maximal at $f = f_{\rm Nyq}$. It follows with the given equation that |
:$${\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | :$${\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - | ||
\frac{\kappa}{T}) | \frac{\kappa}{T}) | ||
|^2}$$ | |^2}$$ | ||
| − | + | is minimal at the Nyquist frequency. However, for $f = f_{\rm Nyq}$, of the infinite sum, only the terms with $\kappa = 0$ and $\kappa = 1$ contribute relevantly to the result. | |
| − | * | + | *From this follows further with the result from '''(1)''': |
:$${\rm Max} \left [ H_{\rm TF}(f) \right ] \ = \ H_{\rm TF}(f = f_{\rm | :$${\rm Max} \left [ H_{\rm TF}(f) \right ] \ = \ H_{\rm TF}(f = f_{\rm | ||
Nyq})= | Nyq})= | ||
| Line 99: | Line 99: | ||
| − | '''(3)''' | + | '''(3)''' Approximating the integral over $H_{\rm TF}(f)$ by the triangular area plotted in the graph, we obtain: |
:$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot | :$$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot | ||
\int_{0}^{1/T} H_{\rm TF}(f) \,{\rm d} f \approx T \cdot | \int_{0}^{1/T} H_{\rm TF}(f) \,{\rm d} f \approx T \cdot | ||
| Line 106: | Line 106: | ||
| − | '''(4)''' | + | '''(4)''' According to the given equation, we obtain for the (mean) symbol error probability: |
:$$p_{\rm S} = {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T}{N_0 \cdot \sigma_{d,\hspace{0.05cm} {\rm norm}}^2}} \right | :$$p_{\rm S} = {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T}{N_0 \cdot \sigma_{d,\hspace{0.05cm} {\rm norm}}^2}} \right | ||
) = {\rm Q}\left ( \sqrt{\frac{10^{8}}{1.7 | ) = {\rm Q}\left ( \sqrt{\frac{10^{8}}{1.7 | ||
| Line 113: | Line 113: | ||
\hspace{0.3cm} p_{\rm S} \hspace{0.15cm}\underline {\approx 0.8 \%} \hspace{0.05cm}.$$ | \hspace{0.3cm} p_{\rm S} \hspace{0.15cm}\underline {\approx 0.8 \%} \hspace{0.05cm}.$$ | ||
| − | : | + | :Since a Nyquist system is present, the worst–case probability $p_{\rm U}$ is just as large. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
[[Category:Digital Signal Transmission: Exercises|^3.5 Linear Nyquist Equalization^]] | [[Category:Digital Signal Transmission: Exercises|^3.5 Linear Nyquist Equalization^]] | ||
Revision as of 09:15, 26 May 2022
We assume the following for this exercise:
- binary bipolar NRZ rectangular pulses
- $$|H_{\rm S}(f)|= {\rm sinc}(f T) \hspace{0.05cm},$$
- coaxial cable with cable attenuation $a_* = 9.2 \ {\rm Np} \ (\approx 80 \ \rm dB)$:
- $$|H_{\rm K}(f)|= {\rm e}^{ -9.2 \cdot \sqrt{2 \cdot |f| \cdot T} }\hspace{0.05cm},$$
- optimal Nyquist equalizer consisting of matched filter and transversal filter:
- $$H_{\rm E}(f) = H_{\rm MF}(f) \cdot H_{\rm TF}(f)$$
- $$\hspace{0.8cm}{\rm where}\hspace{0.2cm}H_{\rm MF}(f) = H_{\rm S}^{\star}(f) \cdot H_{\rm K}^{\star}(f)\hspace{0.05cm},\hspace{0.2cm} H_{\rm TF}(f) = \frac{1}{\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - {\kappa}/{T}) |^2}\hspace{0.05cm}.$$
- Here, $H_{\rm SK}(f) = H_{\rm S}(f) \cdot H_{\rm K}(f)$ denotes the product of transmitter and channel frequency response.
Because of Nyquist equalization, the eye is maximally open. For the error probability holds:
- $$p_{\rm S} \left ( = p_{\rm U} \right ) = {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T}{N_0 \cdot \sigma_{d,\hspace{0.05cm} {\rm norm}}^2}} \right ) \hspace{0.05cm}.$$
The normalized interference power at the decision is given by the following equations:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot \int_{-\infty}^{+\infty} |H_{\rm E}(f)|^2 \,{\rm d} f \hspace{0.5cm} = \hspace{0.5cm} \sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot \int_{-1/(2T)}^{+1/(2T)} H_{\rm TF}(f) \,{\rm d} f \hspace{0.5cm}= \hspace{0.5cm}T \cdot \int_{0}^{1/T} H_{\rm TF}(f) \,{\rm d} f \hspace{0.05cm}.$$
The validity of this equation follows from the periodicity of the transversal filter frequency response $H_{\rm TF}(f)$.
- In the graph, the normalized noise power can be seen as the area highlighted in red.
- As an approximation, the normalized noise power can be calculated by the triangular area shown in blue in the graph.
Notes:
- The exercise belongs to the chapter "Linear Nyquist Equalization".
- To determine the error probability you can use the interactive calculation module "Complementary Gaussian Error Functions".
Questions
Solution
- $$|H_{\rm SK}(f)|= {\rm sinc}(f T) \cdot {\rm e}^{ -9.2 \cdot \sqrt{2 \cdot |f| \cdot T} }\hspace{0.05cm}.$$
- This gives the special cases we are looking for:
- $$f= 0 \text{:} \ \hspace{0.1cm}|H_{\rm SK}(f = 0)|= {\rm sinc}(0) \cdot {\rm e}^0 \hspace{0.15cm}\underline {= 1} \hspace{0.05cm},$$
- $$ f= f_{\rm Nyq}\text{:} \ \hspace{0.1cm}|H_{\rm SK}(f = \frac{1}{2T})|= {\rm sinc}({1}/{2}) \cdot {\rm e}^{-9.2} \hspace{0.15cm}\underline { \approx 6.43 \cdot 10^{-5}} \hspace{0.05cm},$$
- $$ f= {1}/{T} \text{:}\ \hspace{0.1cm}|H_{\rm SK}(f = \frac{1}{T})|= {\rm sinc}({1}) \cdot {\rm e}^{...} \hspace{0.15cm}\underline { = 0} \hspace{0.05cm}.$$
(2) The graph shows that $H_{\rm TF}(f)$ becomes maximal at $f = f_{\rm Nyq}$. It follows with the given equation that
- $${\sum\limits_{\kappa = -\infty}^{+\infty} |H_{\rm SK}(f - \frac{\kappa}{T}) |^2}$$
is minimal at the Nyquist frequency. However, for $f = f_{\rm Nyq}$, of the infinite sum, only the terms with $\kappa = 0$ and $\kappa = 1$ contribute relevantly to the result.
- From this follows further with the result from (1):
- $${\rm Max} \left [ H_{\rm TF}(f) \right ] \ = \ H_{\rm TF}(f = f_{\rm Nyq})= {1}/{2 \cdot |H_{\rm SK}(f = f_{\rm Nyq}) |^2} = \ \frac{1}{2 \cdot (6.43 \cdot 10^{-5})^2}= \frac{10^{10}}{82.69} \hspace{0.15cm}\underline {\approx 1.21 \cdot 10^{8}} \hspace{0.05cm}.$$
(3) Approximating the integral over $H_{\rm TF}(f)$ by the triangular area plotted in the graph, we obtain:
- $$\sigma_{d,\hspace{0.05cm} {\rm norm}}^2 = T \cdot \int_{0}^{1/T} H_{\rm TF}(f) \,{\rm d} f \approx T \cdot \frac{1}{2}\cdot 1.21 \cdot 10^{8}\cdot (0.64 -0.36)\hspace{0.15cm}\underline {\approx 1.7 \cdot 10^{7}} \hspace{0.05cm}.$$
(4) According to the given equation, we obtain for the (mean) symbol error probability:
- $$p_{\rm S} = {\rm Q}\left ( \sqrt{\frac{s_0^2 \cdot T}{N_0 \cdot \sigma_{d,\hspace{0.05cm} {\rm norm}}^2}} \right ) = {\rm Q}\left ( \sqrt{\frac{10^{8}}{1.7 \cdot 10^{7}}} \right ) \approx {\rm Q}(2.42)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_{\rm S} \hspace{0.15cm}\underline {\approx 0.8 \%} \hspace{0.05cm}.$$
- Since a Nyquist system is present, the worst–case probability $p_{\rm U}$ is just as large.