Difference between revisions of "Linear and Time Invariant Systems/Inverse Laplace Transform"
(Die Seite wurde neu angelegt: „ {{Header |Untermenü=Beschreibung kausaler realisierbarer Systeme |Vorherige Seite=Laplace–Transformation und p–Übertragungsfunktion |Nächste Seite=Ein…“) |
|||
| Line 20: | Line 20: | ||
*Ebenso ist der '''Kapazitätsbelag''' $C'$ eine infinitesimal kleine Größe, der ebenso wie $L'$ nur relativ wenig von der Frequenz abhängt. | *Ebenso ist der '''Kapazitätsbelag''' $C'$ eine infinitesimal kleine Größe, der ebenso wie $L'$ nur relativ wenig von der Frequenz abhängt. | ||
*Der '''Ableitungsbelag''' $G'$ berücksichtigt die Verluste des Dielektrikums zwischen den Drähten. Er nimmt etwa proportional mit der Frequenz zu. | *Der '''Ableitungsbelag''' $G'$ berücksichtigt die Verluste des Dielektrikums zwischen den Drähten. Er nimmt etwa proportional mit der Frequenz zu. | ||
| − | *Den weitaus größten Einfluss auf die Signalübertragung hat der Widerstandsbelag $R'$, der für hohe Frequenzen aufgrund des dann dominanten Skineffekts nahezu proportional mit der Wurzel der Frequenz ansteigt. | + | *Den weitaus größten Einfluss auf die Signalübertragung hat der Widerstandsbelag $R'$, der für hohe Frequenzen aufgrund des dann dominanten Skineffekts nahezu proportional mit der Wurzel der Frequenz ansteigt. |
| + | |||
| + | ==Ersatzschaltbild eines kurzen Leitungsabschnitts (2)== | ||
| + | Aus den Maschen– und Knotengleichungen des Leitungsabschnitts ergeben sich mit $ω = 2πf$ die beiden Differenzengleichungen | ||
| + | $$ \begin{align*} U & = I \cdot (R' + {\rm j} \cdot \omega L') \cdot {\rm d}x + (U + {\rm d}U)\hspace{0.05cm},\\ I & = (U + {\rm d}U) \cdot (G' + {\rm j} \cdot \omega C') \cdot {\rm d}x + (I + {\rm d}I)\hspace{0.05cm} \end{align*}$$. | ||
| + | Für einen sehr kurzen Leitungsabschnitt (infinitesimal kleines $dx$) und bei Vernachlässigung der kleinen Größen zweiter Ordnung (zum Beispiel $dU · dx$) kann man nun zwei Differentialquotienten bilden, deren gemeinsame Betrachtung zu einer linearen Differentialgleichung zweiter Ordnung führt: | ||
| + | $$\frac{ {\rm d}U}{ {\rm d}x} = - (R' + {\rm j} \cdot \omega L') \cdot I,\hspace{0.5cm} \frac{ {\rm d}I}{ {\rm d}x} = - (G' + {\rm j} \cdot \omega C') | ||
| + | \cdot U$$ | ||
| + | $$\Rightarrow \hspace{0.3cm}\frac{{\rm d}^2U}{{\rm d}x^2} = (R' + {\rm j} \cdot \omega L') \cdot (G' + {\rm j} \cdot \omega C') | ||
| + | \cdot U\hspace{0.05cm}.$$ | ||
| + | Die Lösung dieser Differentialgleichung lautet: | ||
Revision as of 18:02, 9 May 2016
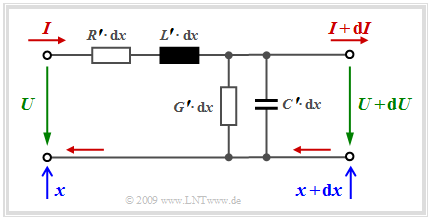
Ersatzschaltbild eines kurzen Leitungsabschnitts (1)
Zur Herleitung der Leitungsgleichungen wird zunächst ein sehr kurzer Leitungsabschnitt der Länge $dx$ betrachtet, so dass sich die Werte für Spannung und Strom am Leitungsanfang $(U$ bzw. $I$ bei $x)$ und am Leitungsende $(U + dU$ sowie $I + dI$ bei $x + dx)$ nur geringfügig unterscheiden. Die Grafik zeigt das zugrundeliegende Modell.
Anders ausgedrückt: Die Leitungslänge $dx$ sei sehr klein gegenüber der Wellenlänge der sich entlang der Leitung ausbreitenden elektromagnetischen Welle, die sich ergibt, da
- mit dem Strom ein magnetisches Feld verbunden ist,
- die Spannung zwischen den Leitern ein elektrisches Feld bewirkt.
Alle infinitesimalen „Bauelemente” im oben skizzierten Ersatzschaltbild sind bei homogenen Leitungen ortsunabhängig:
- Die Induktivität des betrachteten Leitungsabschnitts beträgt $L' · dx$, wobei man die auf die Länge $dx$ bezogene Größe als Induktivitätsbelag bezeichnet.
- Ebenso ist der Kapazitätsbelag $C'$ eine infinitesimal kleine Größe, der ebenso wie $L'$ nur relativ wenig von der Frequenz abhängt.
- Der Ableitungsbelag $G'$ berücksichtigt die Verluste des Dielektrikums zwischen den Drähten. Er nimmt etwa proportional mit der Frequenz zu.
- Den weitaus größten Einfluss auf die Signalübertragung hat der Widerstandsbelag $R'$, der für hohe Frequenzen aufgrund des dann dominanten Skineffekts nahezu proportional mit der Wurzel der Frequenz ansteigt.
Ersatzschaltbild eines kurzen Leitungsabschnitts (2)
Aus den Maschen– und Knotengleichungen des Leitungsabschnitts ergeben sich mit $ω = 2πf$ die beiden Differenzengleichungen $$ \begin{align*} U & = I \cdot (R' + {\rm j} \cdot \omega L') \cdot {\rm d}x + (U + {\rm d}U)\hspace{0.05cm},\\ I & = (U + {\rm d}U) \cdot (G' + {\rm j} \cdot \omega C') \cdot {\rm d}x + (I + {\rm d}I)\hspace{0.05cm} \end{align*}$$. Für einen sehr kurzen Leitungsabschnitt (infinitesimal kleines $dx$) und bei Vernachlässigung der kleinen Größen zweiter Ordnung (zum Beispiel $dU · dx$) kann man nun zwei Differentialquotienten bilden, deren gemeinsame Betrachtung zu einer linearen Differentialgleichung zweiter Ordnung führt: $$\frac{ {\rm d}U}{ {\rm d}x} = - (R' + {\rm j} \cdot \omega L') \cdot I,\hspace{0.5cm} \frac{ {\rm d}I}{ {\rm d}x} = - (G' + {\rm j} \cdot \omega C') \cdot U$$ $$\Rightarrow \hspace{0.3cm}\frac{{\rm d}^2U}{{\rm d}x^2} = (R' + {\rm j} \cdot \omega L') \cdot (G' + {\rm j} \cdot \omega C') \cdot U\hspace{0.05cm}.$$ Die Lösung dieser Differentialgleichung lautet: