Difference between revisions of "Aufgaben:Exercise 3.12: Trellis Diagram for Two Precursors"
From LNTwww
| Line 66: | Line 66: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' The first | + | '''(1)''' The first metric is calculated as follows: |
:$$\varepsilon_{2}(010) = [d_0 - 0 \cdot g_0 - 1 \cdot g_{-1}- 0 \cdot g_{-2}]^2= [0.2 -0.3]^2\hspace{0.15cm}\underline {=0.01} | :$$\varepsilon_{2}(010) = [d_0 - 0 \cdot g_0 - 1 \cdot g_{-1}- 0 \cdot g_{-2}]^2= [0.2 -0.3]^2\hspace{0.15cm}\underline {=0.01} | ||
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| − | Correspondingly, for the other | + | Correspondingly, for the other metrics: |
:$$\varepsilon_{2}(011) \ = \ [0.2 -0.3- 0.2]^2\hspace{0.15cm}\underline {=0.09}\hspace{0.05cm},$$ | :$$\varepsilon_{2}(011) \ = \ [0.2 -0.3- 0.2]^2\hspace{0.15cm}\underline {=0.09}\hspace{0.05cm},$$ | ||
:$$\varepsilon_{2}(110) \ = \ [0.2 -0.5- 0.3]^2\hspace{0.15cm}\underline {=0.36}\hspace{0.05cm},$$ | :$$\varepsilon_{2}(110) \ = \ [0.2 -0.5- 0.3]^2\hspace{0.15cm}\underline {=0.36}\hspace{0.05cm},$$ | ||
| Line 86: | Line 86: | ||
| − | '''(3)''' The <u>first and last solutions</u> are correct: | + | '''(3)''' The <u>first and last solutions</u> are correct: |
| − | *The sequence $1011010$ can be recognized from the continuous path: "red – blue – red – red – blue – red – blue". | + | *The sequence "$1011010$" can be recognized from the continuous path: "red – blue – red – red – blue – red – blue". |
| − | *On the other hand, no final statement can be made about the symbol $a_8$ at time $\nu = 8$: | + | |
| − | *Only under the hypothesis $a_9 = 1$ <u>and</u> $a_{\rm 10} = 1$ one would decide for $a_8 = 0$, under other hypotheses for $a_8 = 1$. | + | *On the other hand, no final statement can be made about the symbol $a_8$ at time $\nu = 8$: |
| + | |||
| + | *Only under the hypothesis $a_9 = 1$ <u>and</u> $a_{\rm 10} = 1$ one would decide for $a_8 = 0$, under other hypotheses for $a_8 = 1$. | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Latest revision as of 16:34, 4 July 2022
We assume the basic pulse values $g_0\ne 0$, $g_{\rm –1}\ne 0$ and $g_{\rm –2}\ne 0$:
- This means that the decision on the symbol $a_{\rm \nu}$ is also influenced by the subsequent coefficients $a_{\rm \nu +1}$ and $a_{\rm \nu +2}$.
- Thus, for each time point $\nu$, exactly eight metrics $\varepsilon_{\rm \nu}$ have to be determined, from which the minimum accumulated metrics ${\it \Gamma}_{\rm \nu}(00)$, ${\it \Gamma}_{\rm \nu}(01)$, ${\it \Gamma}_{\rm \nu}(10)$ and ${\it \Gamma}_{\rm \nu}(11)$ can be calculated.
- For example, ${\it \Gamma}_{\rm \nu}(01)$ provides information about the symbol $a_{\rm \nu}$ under the assumption that $a_{\rm \nu +1} = 0$ and $a_{\rm \nu +2} = 1$ will be.
- Here, the minimum accumulated metric ${\it \Gamma}_{\rm \nu}(01)$ is the smaller value obtained from the comparison of
- $$\big[{\it \Gamma}_{\nu-1}(00) + \varepsilon_{\nu}(001)\big] \hspace{0.15cm}{\rm and} \hspace{0.15cm}\big[{\it \Gamma}_{\nu-1}(10) + \varepsilon_{\nu}(101)\big].$$
To calculate the minimum accumulated metric ${\it \Gamma}_2(10)$ in subtasks (1) and (2), assume the following numerical values:
- unipolar amplitude coefficients: $a_{\rm \nu} ∈ \{0, 1\}$,
- basic pulse values $g_0 = 0.5$, $g_{\rm –1} = 0.3$, $g_{\rm –2} = 0.2$,
- applied noisy detection sample: $d_2 = 0.2$,
- minimum accumulated metric at time $\nu = 1$:
- $${\it \Gamma}_{1}(00) = 0.0,\hspace{0.2cm}{\it \Gamma}_{1}(01) = 0.2, \hspace{0.2cm} {\it \Gamma}_{1}(10) = 0.6,\hspace{0.2cm}{\it \Gamma}_{1}(11) = 1.2 \hspace{0.05cm}.$$
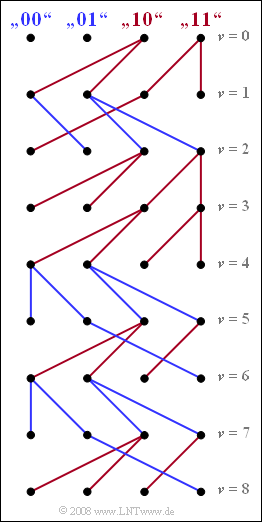
The graph shows the simplified trellis diagram for time points $\nu = 1$ to $\nu = 8$.
- Blue branches come from either ${\it \Gamma}_{\rm \nu –1}(00)$ or ${\it \Gamma}_{\rm \nu –1}(01)$ and denote a hypothetical "$0$".
- In contrast, all red branches – starting from the ${\it \Gamma}_{\rm \nu –1}(10)$ or ${\it \Gamma}_{\rm \nu –1}(11)$ states – indicate the symbol "$1$".
Notes:
- The exercise belongs to the chapter "Viterbi Receiver".
- All quantities here are to be understood normalized.
- Also, assume unipolar and equal probability amplitude coefficients: ${\rm Pr} (a_\nu = 0) = {\rm Pr} (a_\nu = 1)= 0.5.$
Questions
Solution
(1) The first metric is calculated as follows:
- $$\varepsilon_{2}(010) = [d_0 - 0 \cdot g_0 - 1 \cdot g_{-1}- 0 \cdot g_{-2}]^2= [0.2 -0.3]^2\hspace{0.15cm}\underline {=0.01} \hspace{0.05cm}.$$
Correspondingly, for the other metrics:
- $$\varepsilon_{2}(011) \ = \ [0.2 -0.3- 0.2]^2\hspace{0.15cm}\underline {=0.09}\hspace{0.05cm},$$
- $$\varepsilon_{2}(110) \ = \ [0.2 -0.5- 0.3]^2\hspace{0.15cm}\underline {=0.36}\hspace{0.05cm},$$
- $$\varepsilon_{2}(111) \ = \ [0.2 -0.5- 0.3-0.2]^2\hspace{0.15cm}\underline {=0.64} \hspace{0.05cm}.$$
(2) The task is to find the minimum value of each of two comparison values:
- $${\it \Gamma}_{2}(10) \ = \ {\rm Min}\left[{\it \Gamma}_{1}(01) + \varepsilon_{2}(010), \hspace{0.2cm}{\it \Gamma}_{1}(11) + \varepsilon_{2}(110)\right] = {\rm Min}\left[0.2+ 0.01, 1.2 + 0.36\right]\hspace{0.15cm}\underline {= 0.21} \hspace{0.05cm},$$
- $${\it \Gamma}_{2}(11) \ = \ {\rm Min}\left[{\it \Gamma}_{1}(01) + \varepsilon_{2}(011), \hspace{0.2cm}{\it \Gamma}_{1}(11) + \varepsilon_{2}(111)\right] = {\rm Min}\left[0.2+ 0.09, 1.2 + 0.64\right]\hspace{0.15cm}\underline {= 0.29} \hspace{0.05cm}.$$
(3) The first and last solutions are correct:
- The sequence "$1011010$" can be recognized from the continuous path: "red – blue – red – red – blue – red – blue".
- On the other hand, no final statement can be made about the symbol $a_8$ at time $\nu = 8$:
- Only under the hypothesis $a_9 = 1$ and $a_{\rm 10} = 1$ one would decide for $a_8 = 0$, under other hypotheses for $a_8 = 1$.