Difference between revisions of "Aufgaben:Exercise 4.1: About the Gram-Schmidt Process"
m (Guenter moved page Eercise 4.1: About the Gram-Schmidt Process to Exercise 4.1: About the Gram-Schmidt Process) |
|
(No difference)
| |
Latest revision as of 13:56, 13 July 2022
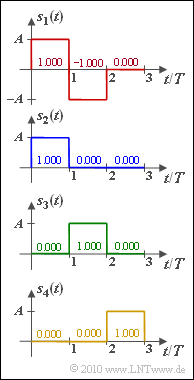
For the four signals $s_1(t), \, \text{...} \, , s_4(t)$ defined by the figure, the three resulting basis functions $\varphi_1(t)$, $\varphi_2(t)$ and $\varphi_3(t)$ are to be determined by applying the Gram-Schmidt process, so that for the signals with $i = 1, \, \text{...} \, , 4$ can be written:
- $$s_i(t) = s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) + s_{i3} \cdot \varphi_3(t)\hspace{0.05cm}.$$
- In subtask (1), let $A^2 = 1 \ \rm mW$ and $T = 1 \ \rm µ s$.
- In the later subtasks, the amplitude and the time are normalized quantities: $A = 1$, $T = 1$.
- Thus, both the coefficients $s_{\it ij}$ and the basis functions $\varphi_{\it j}(t)$ $($with $j = 1,\ 2,\ 3)$ are dimensionless quantities.
Notes:
- The exercise belongs to the chapter "Signals, Basis Functions and Vector Spaces".
- Reference is made in particular to the sections "Orthonormal basis functions" and "Gram-Schmidt process".
Questions
Solution
- Every orthonormal basis function should have energy $1$, that is, it must hold:
- $$||\varphi_j(t)||^2 = \int_{-\infty}^{+\infty}\varphi_j(t)^2\,{\rm d} t = 1 \hspace{0.05cm}.$$
- For this condition to be satisfied, the basis function must have unit $\rm \sqrt{\rm s}$.
- Another equation to be considered is
- $$s_i(t) = \sum\limits_{j = 1}^{N}s_{ij} \cdot \varphi_j(t).$$
- Like the parameter $A$, the signals themselves have the unit $\rm \sqrt{\rm W}$.
- Because of the unit $\rm \sqrt{\rm 1/s}$ of $\varphi_{ j}(t)$, this equation can be satisfied with the correct dimension only if the coefficients $s_{\it ij}$ are given with the unit $\rm \sqrt{\rm Ws}$.
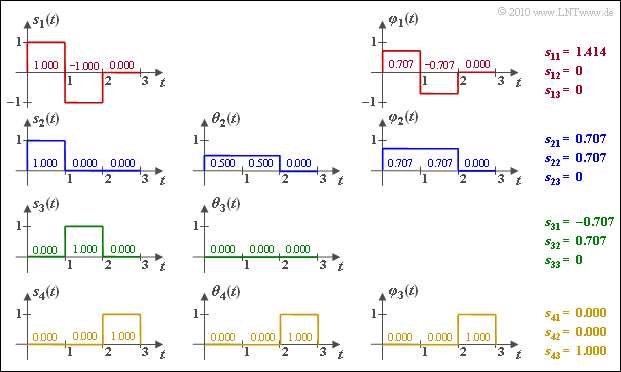
(2) The energy of the signal $s_1(t)$ is equal to $E_1 = 2$.
- It follows for the norm, the basis function $\varphi_1(t)$ and the coefficient $s_{\rm 11}$:
- $$||s_1(t)|| = \sqrt{2},\hspace{0.9cm}\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||},\hspace{0.9cm} s_{11} = \sqrt{E_1} = \sqrt{2} \hspace{0.1cm}\hspace{0.15cm}\underline { {\approx 1.414} } \hspace{0.05cm}.$$
- The other coefficients are $\underline {s_{\rm 12} = s_{\rm 13} = 0}$, since the associated basis functions have not been found at all yet, while $\varphi_1(t)$ is equal in form to $s_1(t)$.
(3) Since at most two basis functions are found after considering $s_2(t)$ ⇒ $s_{\rm 23} \hspace{0.15cm} \underline{= 0}$ holds with certainty. On the other hand one obtains
- for the coefficient
- $$||s_1(t)|| = \sqrt{2},\hspace{0.9cm}\varphi_1(t) = \frac{s_1(t)}{||s_1(t)||},\hspace{0.9cm} s_{11} = \sqrt{E_1} = \sqrt{2} \hspace{0.1cm}\hspace{0.15cm}\underline { {\approx 1.414} } \hspace{0.05cm};$$
- for the auxiliary function $\theta_2(t)$:
- $$\theta_2(t) = s_2(t) - s_{21} \cdot \varphi_1(t) = \left\{ \begin{array}{c} 1 - 0.707 \cdot 0.707 = 0.5\\ 0 - 0.707 \cdot (-0.707) = 0.5 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < 1 \\ 1 \le t < 2 \\ \end{array} \hspace{0.05cm}; $$
- for the second basis function:
- $$\varphi_2(t) = \frac{\theta_2(t)}{||\theta_2(t)||},\hspace{0.2cm} ||\theta_2(t)|| = \sqrt{0.5^2 + 0.5^2} = \sqrt{0.5} \approx 0.707$$
- $$\Rightarrow \hspace{0.3cm} \varphi_2(t) = \left\{ \begin{array}{c} 0.5/0.707 = 0.707\\ 0 \end{array} \right.\quad \begin{array}{*{1}c} 0 \le t < 2 \\ 2 \le t < 3 \\ \end{array} \hspace{0.05cm}; $$
- and finally for the second coefficient
- $$s_{22} = \hspace{0.1cm} < \hspace{-0.1cm} s_2(t), \hspace{0.1cm}\varphi_2(t) \hspace{-0.1cm} > \hspace{0.1cm} = 1 \cdot 0.707 + 0 \cdot 0.707 \hspace{0.1cm}\hspace{0.15cm}\underline { = 0.707} \hspace{0.05cm}.$$
The calculations are illustrated in the graph below.
(4) It can be seen immediately that $s_3(t)$ can be expressed as a linear combination of $s_1(t)$ and $s_2(t)$.
- $$s_{3}(t) = -s_{1}(t) + s_{2}(t),$$
- $$s_{31} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - s_{11} + s_{21} = -1.414 + 0.707 = \hspace{0.1cm}\hspace{0.15cm}\underline {-0.707}\hspace{0.05cm},$$
- $$s_{32} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - s_{12} + s_{22} = 0 + 0.707 \hspace{0.1cm}\underline {= 0.707}\hspace{0.05cm},$$
- $$s_{33} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} - s_{13} + s_{23} = 0 + 0 \hspace{0.1cm}\underline {= 0}\hspace{0.05cm}. $$
(5) The range $2 ≤ t ≤ 3$ is not covered by $\varphi_1(t)$ and $\varphi_2(t)$.
- Therefore, $s_4(t)$ provides the new basis function $\varphi_3(t)$.
- Since $s_4(t)$ has components only in the range $2 ≤ t ≤ 3$ and $||s_4(t)|| = 1$, we obtain $\varphi_3(t) = s_4(t)$ as well as
- $$s_{41} \hspace{0.1cm}\hspace{0.15cm}\underline {= 0}, \hspace{0.2cm}s_{42} \hspace{0.1cm}\hspace{0.15cm}\underline {= 0}, \hspace{0.2cm}s_{43} \hspace{0.1cm}\hspace{0.15cm}\underline { = 1} \hspace{0.05cm}. $$