Aufgaben:Exercise 1.13: Binary Erasure Channel Decoding

• Return to book

Decoding at the BEC Korrektur

We assume here the model in section  "Decoding at the Binary Erasure Channel"  (BEC configuration highlighted in green):

• Each information word  $\underline{u}$  is encoded blockwise and yields the code word  $\underline{x}$.  Let the block code be linear and completely given by its parity-check matrix  $\boldsymbol{\rm H}$.

• During transmission  $n_{\rm E}$  bits of the code word are erased   ⇒  "Binary Erasure Channel"  $\rm (BEC)$.  The code word  $\underline{x}$  thus becomes the received word  $\underline{y}$.

• If the number  $n_{\rm E}$  of erasures is less than the  "minimum distance"  $d_{\rm min}$  of the code,  it is possible to reconstruct from  $\underline{y}$  the code word  $\underline{z} = \underline{x}$  without error,  and thus the correct information word  $\underline{v} = \underline{u}$  is also obtained.

For exercise description,  let us now consider the Hamming code word  $\underline{x} = (0, 1, 0, 1, 1, 0, 0)$  and the received word  $\underline{y} = (0, 1, {\rm E} , {\rm E}, 1, 0, 0).$

• The third and fourth bit were thus erased by the channel.  The  "code word finder"  thus has the task to determine the vector  $z_{\rm E} = (z_{3}, z_{4})$  with  $z_{3}, \ z_{4} \in \{0, 1\}$  to be determined.  This is done according to the equation

$${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T}\hspace{0.05cm}.$$

• In the present example:

$$\underline{z}_{\rm K} = (0, 1, 1, 0, 0)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm K} = \begin{pmatrix} 1 &1 &1 &0 &0\\ 0 &1 &0 &1 &0\\ 1 &1 &0 &0 &1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0\\ 1 &1\\ 0 &1 \end{pmatrix} \hspace{0.05cm}.$$

• This equation gives two equations for the bits to be determined,  whose solution leads to the result  $z_{3} = 0$  and  $z_{4} = 1$.

Hints:

• This exercise belongs to the chapter  "Decoding of Linear Block Codes".

• The algorithm for mapping the received word  $\underline{y}$  to the correct codeword  $\underline{z} = \underline{x}$   is described in detail in the  "theory section" .

• We would like to remind again that in BEC decoding we use the first decoder block  $\underline{y} → \underline{z}$  as  "code word finder"  since wrong decisions are excluded here.  Each received word is decoded correctly,  or it may not be decoded at all.

• In the BSC model,  on the other hand,  decoding errors cannot be avoided.  Accordingly,  we refer to the corresponding block there as  "code word estimator".

Questions

1

  $\underline{y} = (1, {\rm E}, 0, 1, 0, 0, {\rm E})$  was received.  Which sequence does the code word finder decide to use?

	$\underline{z} = (1, 0, 0, 1, 0, 0, 0),$
	$\underline{z} = (1, 1, 0, 1, 0, 0, 1),$
	$\underline{z} = (1, 0, 0, 1, 0, 0, 1).$

2

What are the consequences of the red entries for  $\boldsymbol{\rm H}_{\rm K}$  and  $z_{\rm K}$  (see graphic on the information page)?

	The erasure vector is  $\underline{z}_{\rm E} = (z_{5}, z_{6}, z_{7}).$
	The received word is  $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E}).$
	$\boldsymbol{\rm H}_{\rm E}$  is a  $2 \times 3$  matrix.
	$\boldsymbol{\rm H}_{\rm E}$  is a  $3 \times 3$  matrix.

3

Now apply  $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E}).$  Which code word is selected?

	$\underline{z} = (1, 1, 0, 1, 1, 1, 0),$
	$\underline{z} = (1, 1, 0, 1, 0, 0, 1),$
	$\underline{z} = (1, 1, 0, 0, 0, 1, 0).$
	For the present  $\underline{y}$   no unique decoding is possible.

4

What are the consequences of the green entries for  $\boldsymbol{\rm H}_{\rm K}$  and  $z_{\rm K}$  (see graphic on the information page)?

	The received word is  $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E}).$
	$\boldsymbol{\rm H}_{\rm K}$  differs from subtask  (2)  in the last row.
	$\boldsymbol{\rm H}_{\rm K}$  differs from subtask  (2)  in the last column.

5

Now apply  $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E}).$  Which code word is selected?

	$\underline{z} = (1, 1, 0, 1, 1, 1, 0),$
	$\underline{z} = (1, 1, 0, 1, 0, 0, 1),$
	$\underline{z} = (1, 1, 0, 0, 0, 1, 0).$
	For the present  $\underline{y}$   no unique decoding is possible.

6

Which statements result for the correction capability at the BEC?  $n_{\rm E}$  indicates in the following the number of erasures.

	For  $n_{\rm E} < d_{\rm min}$  unique decoding is always possible.
	For  $n_{\rm E} = d_{\rm min}$  unique decoding is always possible.
	For  $n_{\rm E} = d_{\rm min}$  sometimes a unique decoding is possible.
	For  $n_{\rm E} > d_{\rm min}$  unique decoding is never possible.

Solution

Solution

(1)  The received vector is  $\underline{y} = (1, {\rm E}, 0, 1, 0, 0, {\rm E})$.  Thus,  the code symbols at positions 2 and 7 were erased.  Based on the given parity-check matrix

$${ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &0 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &1 &0 &1 &0 &0 &1 \end{pmatrix}$$

of the Hamming code is obtained for vector and matrix

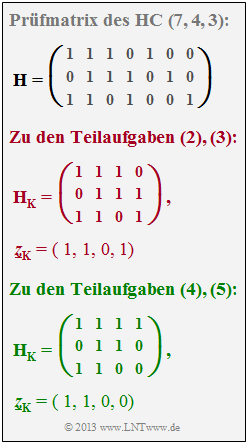
• with respect to all  "correctly transmitted code symbols"  $($index  "$\rm K$"  from German  "korrekt"$)$  which are known to the code word finder:

$$\underline{z}_{\rm K} = (1, 0, 1, 0, 0)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm K} = \begin{pmatrix} 1 &1 &0 &1 &0\\ 0 &1 &1 &0 &1\\ 1 &0 &1 &0 &0 \end{pmatrix} \hspace{0.05cm},$$

• with respect to the two  "erased code symbols"  $z_{2}$  and  $z_{7}$  $($index  $\rm E)$  to be determined:

$$\underline{z}_{\rm E} = (z_2, z_7)\hspace{0.05cm},\hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0\\ 1 &0\\ 1 &1 \end{pmatrix} \hspace{0.05cm}.$$

The equation of determination is thus:

$${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T}= { \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \begin{pmatrix} 1 &0\\ 1 &0\\ 1 &1 \end{pmatrix} \cdot \begin{pmatrix} z_2 \\ z_7 \end{pmatrix} = \begin{pmatrix} 1 &1 &0 &1 &0\\ 0 &1 &1 &0 &1\\ 1 &0 &1 &0 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 0 \\ 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix} \hspace{0.05cm}.$$

This results in three equations for the two unknowns  $z_{2}$  and  $z_{7}$:

$${\rm (a)}\ z_{2} = 1,$$

$${\rm (b)}\ z_{2} = 1,$$

$${\rm (c)}\ z_{2} + z_{7} = 0 \ \Rightarrow \ z_{7}= 1.$$

Thus,  the code word finder returns $\underline{z} = (1, 1, 0, 1, 0, 0, 1)$   ⇒   Suggested solution 2.

(2)  Looking at the given matrix  $\boldsymbol{\rm H}_{\rm K}$,  we see that it coincides with the first four columns of the parity-check matrix  $\boldsymbol{\rm H}$.

• The erasures thus affect the last three bits of the received word   ⇒   $\underline{z}_{\rm E} = (z_{5}, z_{6}, z_{7})$   ⇒   $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E})$.
• The erasure matrix reads:

$${ \boldsymbol{\rm H}}_{\rm E} = \begin{pmatrix} 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} \hspace{0.05cm}.$$

Correct are therefore the  statements 1, 2 and 4.

(3)  One obtains after some matrix multiplications:

$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} = \begin{pmatrix} 1 &1 &1 &0\\ 0 &1 &1 &1\\ 1 &1 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \hspace{0.05cm},\hspace{1cm} { \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T} = \begin{pmatrix} 1 &0 &0\\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} z_5 \\ z_6 \\ z_7 \end{pmatrix} = \begin{pmatrix} z_5 \\ z_6 \\ z_7 \end{pmatrix} \hspace{0.05cm}.$$

• By equating it follows  $z_{5} = 0, \ z_{6} = 0, \ z_{7} = 1$   ⇒   Suggested solution 2.

(4)  The matrix comparison shows that the first three columns of  $\boldsymbol{\rm H}$   and   $\boldsymbol{\rm H}_{\rm K}$   are identical.

• The fourth column of  $\boldsymbol{\rm H}_{\rm K}$  is equal to the fifth column of the parity-check matrix  $\boldsymbol{\rm H}$.

• From this follows for the vector  $z_{\rm E} = (z_{4}, z_{6}, z_{7})$  and further for the received vector  $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E})$   ⇒   Suggested solutions 1 and 3.

(5)  Analogous to subtask  (3),  we obtain:

$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline{z}_{\rm K}^{\rm T} = \begin{pmatrix} 1 &1 &1 &1\\ 0 &1 &1 &0\\ 1 &1 &0 &0 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} \hspace{0.05cm},\hspace{1cm} { \boldsymbol{\rm H}}_{\rm E} \cdot \underline{z}_{\rm E}^{\rm T} = \begin{pmatrix} 0 &0 &0\\ 1 &1 &0\\ 1 &0 &1 \end{pmatrix} \cdot \begin{pmatrix} z_4 \\ z_6 \\ z_7 \end{pmatrix} = \begin{pmatrix} 0 \\ z_4 + z_6 \\ z_4 + z_7 \end{pmatrix} \hspace{0.05cm}.$$

• If we now set the two column vectors equal,  we obtain only two equations for the three unknowns   ⇒   Suggested solution 4.  Or in other words:  

• If the number of extinctions of the BEC channel is larger than the rank of the matrix $\boldsymbol{\rm H}_{\rm E}$,  then no unique solution of the resulting system of equations results.

(6)  To solve this exercise,  we again refer to the systematic Hamming code  $(7, 4, 3)$  according to the given parity-check equation and code table.  Note: 

Code table of the systematic  $(7, 4, 3)$  Hamming code

• The information bits are shown in black and the parity bits in red.  The minimum distance of this code is  $d_{\rm min} = 3$.

• Further we assume that always the code word  $\underline{x} = (1, 1, 0, 1, 0, 0, 1)$  with yellow background was sent.  Then holds:

• If the number  $n_{\rm E}$  of erasures is smaller than  $d_{\rm min} = 3$,  decoding by the method described here is always possible   ⇒   see e.g. subtask  (1)  with  $n_{\rm E}= 2$.

• For  $n_{\rm E} = d_{\rm min} = 3$  decoding is sometimes possible,  see subtask  (3).  In the code table,  there is only one code word that could match   $\underline{y} = (1, 1, 0, 1, {\rm E}, {\rm E}, {\rm E})$   namely the code word highlighted in yellow   $\underline{x} = (1, 1, 0, 1, 0, 0, 1)$ .

• In contrast   $\underline{y} = (1, 1, 0, {\rm E}, 0, {\rm E}, {\rm E})$  according to subtask  (4)  could not be decoded. In the code table, besides  $(1, 1, 0, 1, 0, 0, 1)$  with  $(1, 1, 0, 0, 0, 1, 0)$  one can recognize another code word  (highlighted in green),  which becomes the received word  $\underline{y}$  due to the  $n_{\rm E} = 3$  erasures concerning bit 4, 6 and 7.

• This case,  when the  $n_{\rm E} = d_{\rm min}$  extinctions affect exactly the  $d_{\rm min}$  different bits of two codewords, leads to a matrix  $\mathbf{H}_{\rm E}$  with rank smaller  $d_{\rm min}$.

• If  $\boldsymbol{\rm H}_{\rm E} > d_{\rm min}$, the number  $n - n_{\rm E}$  of bits not erased is smaller than the number  $k$  of information bits.  In this case,  of course,  the code word cannot be decoded.

That is:   Applicable are the  statements 1, 3 and 4.