Difference between revisions of "Aufgaben:Exercise 1.17Z: BPSK Channel Capacity"
| Line 1: | Line 1: | ||
{{quiz-Header|Buchseite=Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding}} | {{quiz-Header|Buchseite=Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding}} | ||
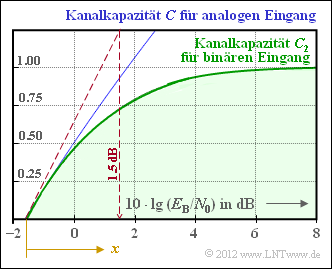
| − | [[File:P_ID2413__KC_Z_1_16.png|right|frame| | + | [[File:P_ID2413__KC_Z_1_16.png|right|frame|For clarification of the BPSK channel capacity]] |
| − | + | According to the [[Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding#Channel_coding_theorem_and_channel_capacity|"channel coding theorem"]] binary signals can be transmitted error-free over the [[Channel_Coding/Channel_Models_and_Decision_Structures#AWGN_channel_at_Binary_Input|"AWGN channel"]] if and only if | |
| − | * | + | *one uses a channel code of rate $R = k/n$ , |
| − | * | + | *the block length $n$ of this code is chosen very large ⇒ $n → ∞$, |
| − | * | + | *the rate $R$ is smaller than the channel capacity valid for binary input $C_{2}$, |
| − | * | + | *where the BPSK channel capacity $C_{2}$ depends on the AWGN quotient $E_{\rm B}/N_{0}$ . |
| − | + | The permissible range for the code rate $R$ is highlighted in green in the graph. The limit curve $C_{2}$, valid for binary input signals $($therefore the index $2)$ and sometimes also referred to as BPSK channel capacity (stands for ''Binary Phase Shift Keying''), however, cannot be specified in mathematically closed form, but is the result of an integral that can only be evaluated numerically. | |
| − | + | As blue curve the channel capacity $C$ is entered, if arbitrary real input signals are allowed. | |
| − | * | + | *For multilevel signals the rate may well assume values $R > 1$ . |
| − | * | + | *For a Gaussian distribution the rate $R$ is the smallest possible $(E_{\rm B}/N_{0})_{\rm min}$ according to the equation |
:$$\left (E_{\rm B}/N_0 \right)_{\rm min} = \frac{2^{2R}-1}{2R}\hspace{0.05cm}.$$ | :$$\left (E_{\rm B}/N_0 \right)_{\rm min} = \frac{2^{2R}-1}{2R}\hspace{0.05cm}.$$ | ||
| − | + | Conversely, the rate $R$ for the given AWGN quotient $E_{\rm B}/N_{0}$ is upper bounded: | |
| − | * | + | *The just allowable code rate $R_{\rm max}$ for a given channel $(E_{\rm B}/N_{0} = \rm const.)$ we refer to as the channel capacity $C$. |
| − | * | + | *For $E_{\rm B}/N_{0} = 1 ⇒ 10 - \ \lg {E_{\rm B}/N_0} = 0 {\rm dB}$ we obtain, for example $C = 0.5$. |
| − | * | + | *This means: Even with the best possible amplitude distribution of the real input signal, the code rate must not exceed $R = 0.5$ . |
| − | * | + | *For binary input, a slightly smaller value results according to $C_{2}.$ |
| − | In | + | In this exercise, try to approximate the graphically given channel capacitance $C_{2}$ by an exponential function: |
| − | * | + | *For the abscissa, use the auxiliary variable (see graph) |
:$$x = \frac {x_0 + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}\hspace{0.05cm}.$$ | :$$x = \frac {x_0 + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}\hspace{0.05cm}.$$ | ||
| − | : | + | :That is, $x$ is without unit; the pseudo unit "$\rm dB$" is omitted. |
| − | * | + | *Consider that for a small $E_{\rm B}/N_{0}$ the approximation $C_{2} \approx C$ is valid (see graph), from which the parameter $x_{0}$ can be determined. |
| − | * | + | *Set for $C_{2}\hspace{0.01cm}' = 1 - {\rm e}^{-a\hspace{0.05cm} · \hspace{0.05cm}x}$ and determine the parameter $a$ from the dashed tangent such that $C_{2}\hspace{0.01cm} ' \approx C$ holds. |
| Line 44: | Line 44: | ||
| − | + | Hints: | |
| − | * | + | * The exercise belongs to the chapter [[Channel_Coding/Information_Theoretical_Limits_of_Channel_Coding|"Information Theoretical Limits of Channel Coding"]]. It complements the [[Aufgaben:Exercise_1.17:_About_the_Channel_Coding_Theorem|"Exercise 1.17"]]. |
| − | * | + | * The "bit/channel access" pseudo-unit of channel capacity is omitted in these exercises. |
| Line 52: | Line 52: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Calculate from the limit for $C → 0$ the curve parameter $x_{0}$? |
|type="{}"} | |type="{}"} | ||
$x_{0} \ = \ $ { 1.6 3% }$\ \rm dB$ | $x_{0} \ = \ $ { 1.6 3% }$\ \rm dB$ | ||
| − | { | + | {Approximate $C_{2}(x)$ by $C_{2}\hspace{0.01cm}'(x) = 1 -{\rm e}^{-a\hspace{0.05cm} · \hspace{0.05cm}x}$. What is the value of $a$? |
|type="{}"} | |type="{}"} | ||
$a \ = \ $ { 0.4 3% } | $a \ = \ $ { 0.4 3% } | ||
| − | { | + | {What channel capacity $C_{2}\hspace{0.01cm}'$ results from this approximation for $E_{\rm B} = N_{0}$ ⇒ $10 · \lg {E_{\rm B} / N_0} = 0 \ {\rm dB}$? |
|type="{}"} | |type="{}"} | ||
$10 · \lg {E_{\rm B} / N_0} = 0 \ {\rm dB} \text{:} \hspace{0.4cm} \ C_{2}\hspace{0.01cm}' \ = \ $ { 0.47 3% } | $10 · \lg {E_{\rm B} / N_0} = 0 \ {\rm dB} \text{:} \hspace{0.4cm} \ C_{2}\hspace{0.01cm}' \ = \ $ { 0.47 3% } | ||
| − | { | + | {Calculate also the channel capacity approximation for the following values: |
|type="{}"} | |type="{}"} | ||
$10 · \lg {E_{\rm B} / N_0} = 2 \ {\rm dB} \text{:} \hspace{0.4cm} \ C_{2}\hspace{0.01cm}' \ = \ $ { 0.76 3% } | $10 · \lg {E_{\rm B} / N_0} = 2 \ {\rm dB} \text{:} \hspace{0.4cm} \ C_{2}\hspace{0.01cm}' \ = \ $ { 0.76 3% } | ||
| Line 74: | Line 74: | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' In the lower $E_{\rm B} /N_{0}$ range, the capacity curves |
| − | *$C_{2}$ ( | + | *$C_{2}$ (valid for binary input, for example BPSK) and |
| − | *$C$ ( | + | *$C$ (valid for analog real-valued input). |
| − | + | converge. For a given rate $R$ $E_{\rm B}/N_{0}$ must be greater than $(2^{2R} - 1)/2R.$ | |
| − | + | The limit transition for $R → 0$ provides the absolute Shannon limit above which error-free transmission is no longer possible: | |
:$${\rm Min}\hspace{0.1cm}\left [E_{\rm B}/N_0 \right] = \lim_{R \rightarrow 0}\hspace{0.1cm} \frac{2^{2R}-1}{2R} = {\rm ln}\hspace{0.1cm}2 \approx 0.693\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | :$${\rm Min}\hspace{0.1cm}\left [E_{\rm B}/N_0 \right] = \lim_{R \rightarrow 0}\hspace{0.1cm} \frac{2^{2R}-1}{2R} = {\rm ln}\hspace{0.1cm}2 \approx 0.693\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 90: | Line 90: | ||
| − | '''(2)''' | + | '''(2)''' The tangent increase at the zero point can be estimated from the graph on the data page: |
:$$\frac{{\rm d}C_2}{{\rm d}x} (x=0) = \frac{1.6 + 1.5}{1.25} =2.48 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} a = \frac{1}{2.48} \hspace{0.15cm} \underline{\approx 0.4}\hspace{0.05cm}.$$ | :$$\frac{{\rm d}C_2}{{\rm d}x} (x=0) = \frac{1.6 + 1.5}{1.25} =2.48 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} a = \frac{1}{2.48} \hspace{0.15cm} \underline{\approx 0.4}\hspace{0.05cm}.$$ | ||
| − | + | Thus, the approximation for the BPSK channel capacity as a function of the abscissa value $x$ is: | |
| − | :$$C_2' = \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}x} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm | + | :$$C_2' = \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}x} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for\hspace{0.15cm}} x > 0, \\{\rm for\hspace{0.15cm}} x < 0. \end{array}$$ |
| − | '''(3)''' | + | '''(3)''' From $E_{\rm B} = N_{0}$ follows $\ 10 · \lg {(E_{\rm B} = N_0)} = 0 \ {\rm dB}$ and $x = 1.6$: |
:$$C_2\hspace{0.01cm}' = 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}1.6}\hspace{0.15cm}\underline{\approx 0.47}\hspace{0.05cm}.$$ | :$$C_2\hspace{0.01cm}' = 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}1.6}\hspace{0.15cm}\underline{\approx 0.47}\hspace{0.05cm}.$$ | ||
| − | '''(4)''' | + | '''(4)''' The corresponding numerical values are: |
:$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{2 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}3.6}\hspace{0.15cm}\underline{\approx 0.76}$$ | :$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{2 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}3.6}\hspace{0.15cm}\underline{\approx 0.76}$$ | ||
:$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{4 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}5.6}\hspace{0.15cm}\underline{\approx 0.89}$$ | :$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{4 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}5.6}\hspace{0.15cm}\underline{\approx 0.89}$$ | ||
:$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}7.6}\hspace{0.15cm}\underline{\approx 0.95}.$$ | :$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}7.6}\hspace{0.15cm}\underline{\approx 0.95}.$$ | ||
| − | + | The values $C_{2}\hspace{0.01cm}'$ of the channel capacity for binary input approximated in this way are somewhat too small. | |
| − | + | From the graph on the information page the exact values $C_{2}$ can be estimated: | |
:$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 =\text{2 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.78}\hspace{0.05cm},$$ | :$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 =\text{2 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.78}\hspace{0.05cm},$$ | ||
| Line 117: | Line 117: | ||
:$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.99}\hspace{0.05cm}.$$ | :$$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.99}\hspace{0.05cm}.$$ | ||
| − | Ab etwa $\ 10 · \lg {(E_{\rm B} / N_0)} = 8 \ {\rm dB}$ gilt innerhalb der Zeichengenauigkeit $C_{2}\hspace{0.01cm}'= C_{2} = 1$ (bit/ | + | Ab etwa $\ 10 · \lg {(E_{\rm B} / N_0)} = 8 \ {\rm dB}$ gilt innerhalb der Zeichengenauigkeit $C_{2}\hspace{0.01cm}'= C_{2} = 1$ (bit/channel use). |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 16:17, 16 August 2022
According to the "channel coding theorem" binary signals can be transmitted error-free over the "AWGN channel" if and only if
- one uses a channel code of rate $R = k/n$ ,
- the block length $n$ of this code is chosen very large ⇒ $n → ∞$,
- the rate $R$ is smaller than the channel capacity valid for binary input $C_{2}$,
- where the BPSK channel capacity $C_{2}$ depends on the AWGN quotient $E_{\rm B}/N_{0}$ .
The permissible range for the code rate $R$ is highlighted in green in the graph. The limit curve $C_{2}$, valid for binary input signals $($therefore the index $2)$ and sometimes also referred to as BPSK channel capacity (stands for Binary Phase Shift Keying), however, cannot be specified in mathematically closed form, but is the result of an integral that can only be evaluated numerically.
As blue curve the channel capacity $C$ is entered, if arbitrary real input signals are allowed.
- For multilevel signals the rate may well assume values $R > 1$ .
- For a Gaussian distribution the rate $R$ is the smallest possible $(E_{\rm B}/N_{0})_{\rm min}$ according to the equation
- $$\left (E_{\rm B}/N_0 \right)_{\rm min} = \frac{2^{2R}-1}{2R}\hspace{0.05cm}.$$
Conversely, the rate $R$ for the given AWGN quotient $E_{\rm B}/N_{0}$ is upper bounded:
- The just allowable code rate $R_{\rm max}$ for a given channel $(E_{\rm B}/N_{0} = \rm const.)$ we refer to as the channel capacity $C$.
- For $E_{\rm B}/N_{0} = 1 ⇒ 10 - \ \lg {E_{\rm B}/N_0} = 0 {\rm dB}$ we obtain, for example $C = 0.5$.
- This means: Even with the best possible amplitude distribution of the real input signal, the code rate must not exceed $R = 0.5$ .
- For binary input, a slightly smaller value results according to $C_{2}.$
In this exercise, try to approximate the graphically given channel capacitance $C_{2}$ by an exponential function:
- For the abscissa, use the auxiliary variable (see graph)
- $$x = \frac {x_0 + 10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 }{1\,{\rm dB}}\hspace{0.05cm}.$$
- That is, $x$ is without unit; the pseudo unit "$\rm dB$" is omitted.
- Consider that for a small $E_{\rm B}/N_{0}$ the approximation $C_{2} \approx C$ is valid (see graph), from which the parameter $x_{0}$ can be determined.
- Set for $C_{2}\hspace{0.01cm}' = 1 - {\rm e}^{-a\hspace{0.05cm} · \hspace{0.05cm}x}$ and determine the parameter $a$ from the dashed tangent such that $C_{2}\hspace{0.01cm} ' \approx C$ holds.
Hints:
- The exercise belongs to the chapter "Information Theoretical Limits of Channel Coding". It complements the "Exercise 1.17".
- The "bit/channel access" pseudo-unit of channel capacity is omitted in these exercises.
Questions
Solution
(1) In the lower $E_{\rm B} /N_{0}$ range, the capacity curves
- $C_{2}$ (valid for binary input, for example BPSK) and
- $C$ (valid for analog real-valued input).
converge. For a given rate $R$ $E_{\rm B}/N_{0}$ must be greater than $(2^{2R} - 1)/2R.$
The limit transition for $R → 0$ provides the absolute Shannon limit above which error-free transmission is no longer possible:
- $${\rm Min}\hspace{0.1cm}\left [E_{\rm B}/N_0 \right] = \lim_{R \rightarrow 0}\hspace{0.1cm} \frac{2^{2R}-1}{2R} = {\rm ln}\hspace{0.1cm}2 \approx 0.693\hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.1cm} {\rm Min}\hspace{0.1cm}\left [E_{\rm B}/N_0 \right] \approx -1.6 \,{\rm dB} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_0 \hspace{0.15cm} \underline{= 1.6 \,{\rm dB}}\hspace{0.05cm}.$$
(2) The tangent increase at the zero point can be estimated from the graph on the data page:
- $$\frac{{\rm d}C_2}{{\rm d}x} (x=0) = \frac{1.6 + 1.5}{1.25} =2.48 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} a = \frac{1}{2.48} \hspace{0.15cm} \underline{\approx 0.4}\hspace{0.05cm}.$$
Thus, the approximation for the BPSK channel capacity as a function of the abscissa value $x$ is:
- $$C_2' = \hspace{0.15cm} \left\{ \begin{array}{c} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}x} \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm for\hspace{0.15cm}} x > 0, \\{\rm for\hspace{0.15cm}} x < 0. \end{array}$$
(3) From $E_{\rm B} = N_{0}$ follows $\ 10 · \lg {(E_{\rm B} = N_0)} = 0 \ {\rm dB}$ and $x = 1.6$:
- $$C_2\hspace{0.01cm}' = 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}1.6}\hspace{0.15cm}\underline{\approx 0.47}\hspace{0.05cm}.$$
(4) The corresponding numerical values are:
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{2 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}3.6}\hspace{0.15cm}\underline{\approx 0.76}$$
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{4 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}5.6}\hspace{0.15cm}\underline{\approx 0.89}$$
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2\hspace{0.01cm}' \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 1 - {\rm e}^{- 0.4 \hspace{0.05cm}\cdot \hspace{0.05cm}7.6}\hspace{0.15cm}\underline{\approx 0.95}.$$
The values $C_{2}\hspace{0.01cm}'$ of the channel capacity for binary input approximated in this way are somewhat too small.
From the graph on the information page the exact values $C_{2}$ can be estimated:
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 =\text{2 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.78}\hspace{0.05cm},$$
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{4 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.94}\hspace{0.05cm},$$
- $$10 \cdot {\rm lg} \hspace{0.1cm} E_{\rm B}/N_0 = \text{6 dB:} \hspace{0.3cm} C_2 \hspace{-0.15cm}\ \approx \ \hspace{-0.15cm} {0.99}\hspace{0.05cm}.$$
Ab etwa $\ 10 · \lg {(E_{\rm B} / N_0)} = 8 \ {\rm dB}$ gilt innerhalb der Zeichengenauigkeit $C_{2}\hspace{0.01cm}'= C_{2} = 1$ (bit/channel use).