Aufgaben:Exercise 4.18: Non-Coherent FSK Demodulation

• Return to book

Non-coherent demodulation

We consider Frequency Shift Keying  (FSK) with  $M = 2$   ⇒   binary signaling. The two low-pass basis functions in this case are complex and are:

$$\xi_1(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$

$$ \xi_2(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{1/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T \hspace{0.05cm}.$$

Then, for the two possible waveforms in the low-pass region, with the mean symbol energy  $E_{\rm S}$:

$$m_0\text{:}\hspace{0.2cm} s_{\rm TP,\hspace{0.05cm}0} = \sqrt{E_{\rm S}} \cdot \xi_1(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\boldsymbol{ s}_{\rm 0} = (\sqrt{E_{\rm S}}, 0)\hspace{0.05cm},$$

$$m_1\text{:}\hspace{0.2cm} s_{\rm TP,\hspace{0.05cm}1} = \sqrt{E_{\rm S}} \cdot \xi_2(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\boldsymbol{ s}_{\rm 1} = (0, \sqrt{E_{\rm S}})\hspace{0.05cm}.$$

Here,  $h$  indicates the so-called modulation index. This must meet certain criteria to result in orthogonal waveforms. However, these criteria depend on whether a coherent or a non-coherent demodulator is used at the receiver.

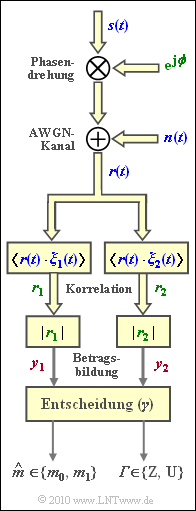
The diagram shows the non-coherent demodulator for binary Frequency Shift Keying  (FSK) in the lower section. All complex signals are labeled in blue, complex values in green, and real values in red.

Compared to the decision process given in the  "theory part",  we now consider a complex decision that outputs a safety flag  ${\it \Gamma} = \{{\rm Z}, \ {\rm U}\}$  in addition to the estimated value. The logical values  ${\rm Z}$  and  ${\rm U}$  stand for a realiable (Zuverlässige) and an Unreliable decision, respectively. Thus, there are four possibilities for the decision, controlled by the parameter  $\gamma$:

$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{0.1cm} m_0,\hspace{0.05cm}{\it \Gamma} = {\rm Z}, \hspace{0.5cm}{\rm falls} \hspace{0.15cm}y_1 > \gamma \cdot y_2\hspace{0.05cm},$$

$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{0.1cm} m_0,\hspace{0.05cm}{\it \Gamma} = {\rm U}, \hspace{0.5cm}{\rm falls} \hspace{0.15cm}y_2 < y_1 < \gamma \cdot y_2\hspace{0.05cm},$$

$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{0.1cm} m_1,\hspace{0.05cm}{\it \Gamma} = {\rm Z}, \hspace{0.5cm}{\rm falls} \hspace{0.15cm}y_2 > \gamma \cdot y_1\hspace{0.05cm},$$

$$\hat{m} \hspace{-0.1cm} \ = \ \hspace{0.1cm} m_1,\hspace{0.05cm}{\it \Gamma} = {\rm U}, \hspace{0.5cm}{\rm falls} \hspace{0.15cm}y_1 < y_2 < \gamma \cdot y_1\hspace{0.05cm}.$$

In the questions for the exercise, the two values  $\gamma = 1$  and  $\gamma = 2$  are considered.

For the probability that the decision erroneously chooses the symbol  $m_1$  and, moreover, indicates that this decision is to be considered reliable (particularly reprehensible), the following applies

$${\rm Pr}\{\hat{m} = m_1,\hspace{0.05cm}{\it \Gamma} = {\rm Z} \hspace{0.05cm}| \hspace{0.05cm}m_0 \} = \frac{1}{1 + \gamma^2} \cdot {\rm exp } \left [ - \frac{\gamma^2 \cdot E_{\rm S}}{(1+\gamma^2) \cdot N_{\rm 0}}\right ] \hspace{0.05cm}.$$

Note:

• The exercise belongs to the topic of the chapter  "Carrier Frequency Systems with Non-Coherent Demodulation".

Questions

1

Which statements are true in the case of coherent demodulation of the FSK?

	Orthogonality results if  $h$  is an integer.
	Orthogonal waveforms also result for  $h = 0.5$.
	Orthogonality cannot be achieved in principle.
	For the AWGN channel  $r(t) = s(t) + n(t)$ is valid.

2

Which statements are true for the non-coherent demodulation of FSK?

	Orthogonality results when  $h$  is an integer.
	Orthogonal waveforms also result for  $h = 0.5$.
	Orthogonality cannot be achieved in principle.
	For the AWGN channel  $r(t) = s(t) + n(t)$ is valid.

3

Let  $E_{\rm S}/N_0 = 10$. What is the error probability, i.e., the probability that the estimated value deviates from the transmitted message?

$p_{\rm S} \ = \ $ $\ \%$

4

Let  $\gamma = 2$  and  $E_{\rm S}/N_0 = 10$. What is the probability that the security feature signals a reliable decision despite the errors?

${\rm Pr}({\it \Gamma} = {\rm Z\hspace{0.05cm} | \hspace{0.05cm}error}) \ = \ $ $\ \cdot 10^{\rm –5}$

5

Furthermore, let  $\gamma = 2$ and  $E_{\rm S}/N_0 = 10$. What is the (conditional) probability that the additional information "unreliable" is displayed in case of an error?

${\rm Pr}({\it \Gamma} = {\rm U\hspace{0.05cm} | \hspace{0.05cm}error}) \ = \ $ $\ \%$

Solution

Solution

(1)  Solutions 1, 2 and 4 are correct:

• In coherent demodulation, orthogonality is given when the modulation index $h$ is a multiple of $0.5$. Binary FSK with $h = 0.5$ is also called Minimum Shift Keying (MSK).
• Since phase control compensates for the phase shift (delay) on the AWGN transmission channel   ⇒   ${\rm e}^{{\rm j}\phi} \cdot {\rm e}^{-{\rm j}\phi} = 1$, the signals in the equivalent low-pass region are actually:   $r(t) = s(t) + n(t) \hspace{0.05cm}.$

(2)  Here, only the first solution is correct, i.e., now $h = 1, \ 2, \ 3, \text{ ...}$ must be an integer.

• So a non-coherent demodulation of FSK is not possible.
• Because of the missing phase control, the following is also true:

$$r(t) = s(t) \cdot {\rm e }^{ - {\rm j }\hspace{0.05cm}\phi} + n(t) \hspace{0.05cm}.$$

(3)  For equally probable messages applies:

$$p_{\rm S} = {\rm Pr}({\cal{E}}) = {\rm Pr}({\cal{E}}| \hspace{0.05cm}m = m_0) = {\rm Pr}(\hat{m}= m_1| \hspace{0.05cm}m = m_0)\hspace{0.05cm}.$$

• This probability is obtained from the given equation with $\gamma = 1$.
• In this case, ${\it \Gamma} ={\rm Z}$ is always and the decision rule is:   Decide on the symbol $m_0$ if $y_1 > y_2$.
• It follows that:

$$p_{\rm S} = \frac{1}{1 + \gamma^2} \cdot {\rm exp } \left [ - \frac{\gamma^2 \cdot E_{\rm S}}{(1+\gamma^2) \cdot N_{\rm 0}}\right ]_{\gamma = 1} = {1}/{2} \cdot {\rm e }^{-E_{\rm S}/(2N_0)}\hspace{0.05cm}.$$

• With $E_{\rm S}/N_0 = 10$, we get $p_{\rm S} = 1/2 \cdot {\rm e}^{\rm –5} \approx \underline {0.337 \cdot \%}$.

(4)  For symmetry reasons, this probability results in

$${\rm Pr}({\it \Gamma} = {\rm Z}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm error} ) = {1}/{2} \cdot {\rm Pr}\{(\hat{m} = m_1)\hspace{0.05cm}\cap\hspace{0.05cm}{\it \Gamma} = {\rm Z} \hspace{0.05cm}| \hspace{0.05cm}m_0 \} + {1}/{2}\cdot {\rm Pr}\{(\hat{m} = m_0)\hspace{0.05cm}\cap\hspace{0.05cm}({\it \Gamma} = {\rm Z}) \hspace{0.05cm}| \hspace{0.05cm}m_1 \} $$

$$\Rightarrow \hspace{0.3cm} {\rm Pr}({\it \Gamma} = {\rm Z}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm error} ) = {\rm Pr}\{(\hat{m} = m_1)\hspace{0.05cm}\cap\hspace{0.05cm}({\it \Gamma} = {\rm Z}) \hspace{0.05cm}| \hspace{0.05cm}m_0 \} =\frac{1}{1 + 2^2} \cdot {\rm exp } \left [ - \frac{2^2 \cdot E_{\rm S}}{(1+2^2) \cdot N_{\rm 0}}\right ] = {1}/{5} \cdot {\rm e }^{-8} = \underline{6.7 \cdot 10^{-5}}\hspace{0.05cm}.$$

(5)  Since ${\rm U}$ and ${\rm Z}$ give a complete system according to statistics, with the results of subtasks (3) and (4):

$${\rm Pr}({\it \Gamma} = {\rm U}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm error} ) ={\rm Pr}( {\rm error} ) - {\rm Pr}({\it \Gamma} = {\rm Z}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm error} ) = 3.37 \cdot 10^{-3} - 6.7 \cdot 10^{-5} = \underline{3.3 \cdot 10^{-3}} \hspace{0.05cm}.$$

• Thus, the conditional probability we are looking for is ${\rm Pr}({\it \Gamma}= {\rm U}\hspace{0.05cm}|\hspace{0.05cm} {\rm error})$:

$${\rm Pr}({\it \Gamma}= {\rm U}\hspace{0.05cm}|\hspace{0.05cm} {\rm error} ) = \frac{{\rm Pr}({\it \Gamma} = {\rm U}\hspace{0.05cm}\cap\hspace{0.05cm} {\rm error} ) }{{\rm Pr}( {\rm error} )} = \frac{3.3 \cdot 10^{-3}}{3.37 \cdot 10^{-3}} \hspace{0.15cm} \underline{= 98 \%} \hspace{0.05cm}.$$