Difference between revisions of "Aufgaben:Exercise 2.10: Reed-Solomon Error Detection"
| Line 83: | Line 83: | ||
===Solution=== | ===Solution=== | ||
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' The equation describing the weights $W_i$ is (the minimum distance $d_{\rm min}$ is abbreviated here as $d$): |
:$$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$ | :$$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$ | ||
| − | + | Because of the minimum distance $d_{\min} = 5$, $W_3 \ \underline{= 0}$ and $W_4 \ \underline{= 0}$. The other weights result in | |
:$$W_5 = {7 \choose 5} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 \cdot4 \cdot 3}{1 \cdot 2 \cdot 3 \cdot4 \cdot 5} \cdot 7 = 21 \cdot 7 | :$$W_5 = {7 \choose 5} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 \cdot4 \cdot 3}{1 \cdot 2 \cdot 3 \cdot4 \cdot 5} \cdot 7 = 21 \cdot 7 | ||
\hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$ | \hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$ | ||
| Line 96: | Line 96: | ||
| − | '''(2)''' | + | '''(2)''' Analogous to subtask (1), we obtain: |
:$$W_3 = {7 \choose 3} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 }{1 \cdot 2 \cdot 3 } \cdot 7 = 35 \cdot 7 | :$$W_3 = {7 \choose 3} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 }{1 \cdot 2 \cdot 3 } \cdot 7 = 35 \cdot 7 | ||
\hspace{0.15cm}\underline {= 245}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline {= 245}\hspace{0.05cm}.$$ | ||
| − | '''(3)''' | + | '''(3)''' The corruption probability of a symbol is given by $\varepsilon_{\rm S} = 0.1$. |
| − | : | + | :Then, for the probability that in a codeword with $n = 7$ code symbols. |
| − | * | + | * exactly 3 symbols are corrupted: |
:$$p_3 = 0.1^3 \cdot 0.9^4 = 0.6561 \cdot 10^{-3} | :$$p_3 = 0.1^3 \cdot 0.9^4 = 0.6561 \cdot 10^{-3} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * | + | * exactly 4 symbols are corrupted: |
:$$p_4 = 0.1^4 \cdot 0.9^3 = 0.729 \cdot 10^{-4} | :$$p_4 = 0.1^4 \cdot 0.9^3 = 0.729 \cdot 10^{-4} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * | + | * exactly 5 symbols are corrupted: |
:$$p_5 = 0.1^5 \cdot 0.9^2 = 0.81 \cdot 10^{-5} | :$$p_5 = 0.1^5 \cdot 0.9^2 = 0.81 \cdot 10^{-5} | ||
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
| − | * | + | * exactly 6 symbols are corrupted: |
:$$p_6 = 0.1^6 \cdot 0.9 = 0.9 \cdot 10^{-6}\hspace{0.05cm},$$ | :$$p_6 = 0.1^6 \cdot 0.9 = 0.9 \cdot 10^{-6}\hspace{0.05cm},$$ | ||
| − | * | + | * all $n = 7$ symbols are corrupted: |
:$$p_7 = 0.1^7 = 10^{-7}\hspace{0.05cm}.$$ | :$$p_7 = 0.1^7 = 10^{-7}\hspace{0.05cm}.$$ | ||
| − | + | At $\rm RSC \, (7, \, 3, \, 5)_8$ the zero word can be corrupted by symbol errors into one of $q^k - 1 = 8^3 - 1 = 511$ other codewords. | |
| − | + | Thus, using the weight enumerating functions of subtask (1), we obtain: | |
:$${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{511} =\frac {147 \cdot 0.81 \cdot 10^{-5} + 147 \cdot 0.9 \cdot 10^{-6} + 217 \cdot 10^{-7}}{511} | :$${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{511} =\frac {147 \cdot 0.81 \cdot 10^{-5} + 147 \cdot 0.9 \cdot 10^{-6} + 217 \cdot 10^{-7}}{511} | ||
\hspace{0.15cm}\underline {\approx 0.263 \cdot 10^{-5}} \hspace{0.05cm}.$$ | \hspace{0.15cm}\underline {\approx 0.263 \cdot 10^{-5}} \hspace{0.05cm}.$$ | ||
| − | + | At $\rm RSC \, (7, \, 5, \, 3)_8$ must be averaged over $8^5 - 1 = 32767$ corruption probabilities because of $k = 5$. | |
| − | + | With $W_3 = 245$ from subtask (2) and the weights $W_4 = 1224, \ W_5 = 5586, \ W_6 = 12838, \ W_7 = 12873$ according to the specification sheet, we obtain for this: | |
| − | :$${\rm Pr}({\rm | + | :$${\rm Pr}({\rm Block\hspace{0.15cm}error}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_3 \cdot p_3 + W_4 \cdot p_4 + W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{32767} =\frac {245 \cdot 0.656 \cdot 10^{-3} + \hspace{0.15cm}... \hspace{0.15cm}+ 12873 \cdot 10^{-7}}{32767} |
\hspace{0.15cm}\underline {\approx 0.942 \cdot 10^{-5}} \hspace{0.05cm}. $$ | \hspace{0.15cm}\underline {\approx 0.942 \cdot 10^{-5}} \hspace{0.05cm}. $$ | ||
| − | '''(4)''' | + | '''(4)''' Let only $d_{\rm min}$ (further abbreviated as $d$) be known and thus also $p_d = \varepsilon_{\rm S}^d \cdot (1 - \varepsilon_{\rm S})^{n-d}$. This is also the upper bound we are looking for: |
| − | * ${\rm RSC} \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} {\rm Pr( | + | * ${\rm RSC} \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} {\rm Pr(Upper \ bound)} = p_5 = \underline{0.81 \cdot 10^{-5}}$, |
| − | * ${\rm RSC} \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} {\rm Pr( | + | * ${\rm RSC} \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} {\rm Pr(Upper \ bound)} = p_3 = \underline{65.6 \cdot 10^{-5}}$. |
| − | + | Since the weight $W_d$ was assumed to be unknown, it is set to the maximum possible value ($W_5 = 511$ or $W_3 = 32767$) so that the prefactors in the equations for subtask (3) disappear. This is the only way to ensure an upper bound. | |
| − | + | In both cases, the upper bound is significantly higher than the results of subtask (3): | |
| − | * $\rm RSC \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} 0.810 \cdot 10^{-5}$ statt $0.263 \cdot 10^{-5}$ (Faktor | + | * $\rm RSC \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} 0.810 \cdot 10^{-5}$ statt $0.263 \cdot 10^{-5}$ (Faktor approx. $3$), |
| − | * $\rm RSC \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} 65.6 \cdot 10^{-5}$ statt $0.942 \cdot 10^{-5}$ (Faktor | + | * $\rm RSC \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} 65.6 \cdot 10^{-5}$ statt $0.942 \cdot 10^{-5}$ (Faktor approx. $70$). |
| − | '''(5)''' | + | '''(5)''' Using the abbreviation $d = d_{\rm min}$, one obtains for the lower bound: |
| − | :$${\rm Pr}({\rm | + | :$${\rm Pr}({\rm Lower\hspace{0.15cm} bound})= \frac{W_d \cdot p_d}{q^k -1} |
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | * | + | * For the $\rm RSC \, (7, \, 3, \, 5)_8$, because of $W_d = W_5$ and $p_d = p_5$, the lower bound is about $11\%$ below the actual value $(0.263 \cdot 10^{-5})$: |
| − | :$${\rm Pr}({\rm | + | :$${\rm Pr}({\rm Lower\hspace{0.15cm} bound}) = \frac{147 \cdot 0.81 \cdot 10^{-5}}{511} |
\hspace{0.15cm}\underline {\approx 0.233 \cdot 10^{-5}}$$ | \hspace{0.15cm}\underline {\approx 0.233 \cdot 10^{-5}}$$ | ||
| − | * | + | * For the $\rm RSC \, (7, \, 5, \, 3)_8$ holds with $W_d = W_3$ and $p_d = p_3$, the lower bound here deviates from the actual value $(0.942 \cdot 10^{-5})$more strongly, because in this code the contributions of the higher weights $(W_4, \ W_5, \ W_6, \ W_7)$ are more relevant in relation to $W_3$: |
| − | :$${\rm Pr}({\rm | + | :$${\rm Pr}({\rm Lower\hspace{0.15cm} bound}) = \frac{245 \cdot 0.656 \cdot 10^{-3}}{32767} |
\hspace{0.15cm}\underline {\approx 0.494 \cdot 10^{-5}}\hspace{0.05cm}.$$ | \hspace{0.15cm}\underline {\approx 0.494 \cdot 10^{-5}}\hspace{0.05cm}.$$ | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 18:55, 2 September 2022
For a linear block code, up to $e = d_{\rm min} - 1$ errors can be detected. For all Reed–Solomon codes the minimum distance is
- $$d_{\rm min} = n-k+1 \hspace{0.05cm}.$$
One must distinguish the following cases:
- If no more than $e = n - k$ symbol errors occur, the block is always detected as faulty.
- Error detection can still work even if more than $n - k$ symbol errors occur, and this is when the received word is not a valid codeword of the Reed–Solomon code:
- $$\underline {y} \notin C_{\rm RS} = \{ \underline {c}_{\hspace{0.05cm}0}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_i, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_{\hspace{0.05cm}n -1} \} \hspace{0.05cm}. $$
- However, if the corrupted received word $(\underline{y} ≠ \underline{c})$ is a valid codeword ⇒ $\underline{y}$, the decoding process will leave the corrupted block undetected.
We define as block error probability:
- $${\rm Pr}({\rm Block\hspace{0.15cm}error}) = {\rm Pr}(\underline {y} \ne \underline {c}) \hspace{0.05cm}.$$
In this exercise, this probability is to be determined for the following codes:
- Reed–Solomon code $(7, \, 3, \, 5)_8 \ \Rightarrow \ d_{\rm min} = 5$,
- Reed–Solomon code $(7, \, 5, \, 3)_8 \ \Rightarrow \ d_{\rm min} = 3$.
Furthermore, let it hold:
- Each symbol is corrupted into another symbol with probability $\varepsilon_{\rm S} = 0.1$ and correctly transferred with probability $1 - \varepsilon_{\rm S} = 0.9$ .
- For the distance spectrum of a Reed–Solomon code of length $n$ holds with $d = d_{\rm min}$:
- $$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$
Besides, two bounds for the block error probability will be considered and evaluated:
- If the minimum distance alone is known, one can derive an upper bound from it. The weight enumerating factors $W_i$ are to be chosen in such a way, that certainly (that is: with all constellations) applies:
- $${\rm Pr}({\rm Upper\hspace{0.15cm} bound}) \ge {\rm Pr}({\rm Block\hspace{0.15cm}error}) \hspace{0.05cm}. $$
- A lower bound additionally requires knowledge of the weight function $W_i$ for $i = d_{\rm min}$. Thus, the following condition can be satisfied:
- $${\rm Pr}({\rm Upper\hspace{0.15cm} bound}) \le {\rm Pr}({\rm Block\hspace{0.15cm}error}) \hspace{0.05cm}.$$
Hints:
- The exercise belongs to the chapter "Definition and Properties of Reed-Solomon Codes".
- Reference is made in particular to the page "Singleton Bound and Minimum Distance".
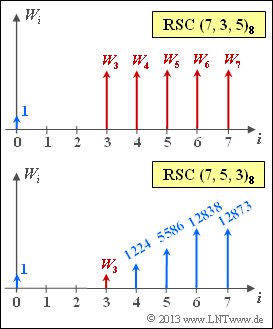
- To be calculated are the weights marked in red in the above graph $W_i$.
Questions
Solution
- $$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$
Because of the minimum distance $d_{\min} = 5$, $W_3 \ \underline{= 0}$ and $W_4 \ \underline{= 0}$. The other weights result in
- $$W_5 = {7 \choose 5} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 \cdot4 \cdot 3}{1 \cdot 2 \cdot 3 \cdot4 \cdot 5} \cdot 7 = 21 \cdot 7 \hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$
- $$W_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 6} \cdot \sum_{j = 0}^{1}\hspace{0.15cm}(-1)^j \cdot {6 \choose j} \cdot \big (\hspace{0.03cm}8^{2\hspace{0.03cm}-\hspace{0.03cm}j} -1 \big )=7 \cdot \left [ (8^2 - 1) - 6 \cdot (8^1 - 1)\right ] = 7 \cdot (63-42) \hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$
- $$W_7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 7} \cdot \sum_{j = 0}^{2}\hspace{0.15cm}(-1)^j \cdot {7 \choose j} \cdot \big (\hspace{0.03cm}8^{3\hspace{0.03cm}-\hspace{0.03cm}j} -1 \big )= (8^3 - 1) - 7 \cdot (8^2 - 1) +21 \cdot (8^1 - 1) = 511 - 7 \cdot 63 + 21 \cdot 7 \hspace{0.15cm}\underline {= 217}\hspace{0.05cm},$$
- $$\Rightarrow \hspace{0.3cm}W_0 + W_5 + W_6 + W_7 = 1 + 147 + 147 + 217 = 512 = 8^3 = q^k\hspace{0.05cm}.$$
(2) Analogous to subtask (1), we obtain:
- $$W_3 = {7 \choose 3} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 }{1 \cdot 2 \cdot 3 } \cdot 7 = 35 \cdot 7 \hspace{0.15cm}\underline {= 245}\hspace{0.05cm}.$$
(3) The corruption probability of a symbol is given by $\varepsilon_{\rm S} = 0.1$.
- Then, for the probability that in a codeword with $n = 7$ code symbols.
- exactly 3 symbols are corrupted:
- $$p_3 = 0.1^3 \cdot 0.9^4 = 0.6561 \cdot 10^{-3} \hspace{0.05cm},$$
- exactly 4 symbols are corrupted:
- $$p_4 = 0.1^4 \cdot 0.9^3 = 0.729 \cdot 10^{-4} \hspace{0.05cm},$$
- exactly 5 symbols are corrupted:
- $$p_5 = 0.1^5 \cdot 0.9^2 = 0.81 \cdot 10^{-5} \hspace{0.05cm},$$
- exactly 6 symbols are corrupted:
- $$p_6 = 0.1^6 \cdot 0.9 = 0.9 \cdot 10^{-6}\hspace{0.05cm},$$
- all $n = 7$ symbols are corrupted:
- $$p_7 = 0.1^7 = 10^{-7}\hspace{0.05cm}.$$
At $\rm RSC \, (7, \, 3, \, 5)_8$ the zero word can be corrupted by symbol errors into one of $q^k - 1 = 8^3 - 1 = 511$ other codewords.
Thus, using the weight enumerating functions of subtask (1), we obtain:
- $${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{511} =\frac {147 \cdot 0.81 \cdot 10^{-5} + 147 \cdot 0.9 \cdot 10^{-6} + 217 \cdot 10^{-7}}{511} \hspace{0.15cm}\underline {\approx 0.263 \cdot 10^{-5}} \hspace{0.05cm}.$$
At $\rm RSC \, (7, \, 5, \, 3)_8$ must be averaged over $8^5 - 1 = 32767$ corruption probabilities because of $k = 5$.
With $W_3 = 245$ from subtask (2) and the weights $W_4 = 1224, \ W_5 = 5586, \ W_6 = 12838, \ W_7 = 12873$ according to the specification sheet, we obtain for this:
- $${\rm Pr}({\rm Block\hspace{0.15cm}error}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_3 \cdot p_3 + W_4 \cdot p_4 + W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{32767} =\frac {245 \cdot 0.656 \cdot 10^{-3} + \hspace{0.15cm}... \hspace{0.15cm}+ 12873 \cdot 10^{-7}}{32767} \hspace{0.15cm}\underline {\approx 0.942 \cdot 10^{-5}} \hspace{0.05cm}. $$
(4) Let only $d_{\rm min}$ (further abbreviated as $d$) be known and thus also $p_d = \varepsilon_{\rm S}^d \cdot (1 - \varepsilon_{\rm S})^{n-d}$. This is also the upper bound we are looking for:
- ${\rm RSC} \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} {\rm Pr(Upper \ bound)} = p_5 = \underline{0.81 \cdot 10^{-5}}$,
- ${\rm RSC} \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} {\rm Pr(Upper \ bound)} = p_3 = \underline{65.6 \cdot 10^{-5}}$.
Since the weight $W_d$ was assumed to be unknown, it is set to the maximum possible value ($W_5 = 511$ or $W_3 = 32767$) so that the prefactors in the equations for subtask (3) disappear. This is the only way to ensure an upper bound.
In both cases, the upper bound is significantly higher than the results of subtask (3):
- $\rm RSC \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} 0.810 \cdot 10^{-5}$ statt $0.263 \cdot 10^{-5}$ (Faktor approx. $3$),
- $\rm RSC \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} 65.6 \cdot 10^{-5}$ statt $0.942 \cdot 10^{-5}$ (Faktor approx. $70$).
(5) Using the abbreviation $d = d_{\rm min}$, one obtains for the lower bound:
- $${\rm Pr}({\rm Lower\hspace{0.15cm} bound})= \frac{W_d \cdot p_d}{q^k -1} \hspace{0.05cm}. $$
- For the $\rm RSC \, (7, \, 3, \, 5)_8$, because of $W_d = W_5$ and $p_d = p_5$, the lower bound is about $11\%$ below the actual value $(0.263 \cdot 10^{-5})$:
- $${\rm Pr}({\rm Lower\hspace{0.15cm} bound}) = \frac{147 \cdot 0.81 \cdot 10^{-5}}{511} \hspace{0.15cm}\underline {\approx 0.233 \cdot 10^{-5}}$$
- For the $\rm RSC \, (7, \, 5, \, 3)_8$ holds with $W_d = W_3$ and $p_d = p_3$, the lower bound here deviates from the actual value $(0.942 \cdot 10^{-5})$more strongly, because in this code the contributions of the higher weights $(W_4, \ W_5, \ W_6, \ W_7)$ are more relevant in relation to $W_3$:
- $${\rm Pr}({\rm Lower\hspace{0.15cm} bound}) = \frac{245 \cdot 0.656 \cdot 10^{-3}}{32767} \hspace{0.15cm}\underline {\approx 0.494 \cdot 10^{-5}}\hspace{0.05cm}.$$