Difference between revisions of "Aufgaben:Exercise 2.14: Petersen Algorithm?"
From LNTwww
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding}} |
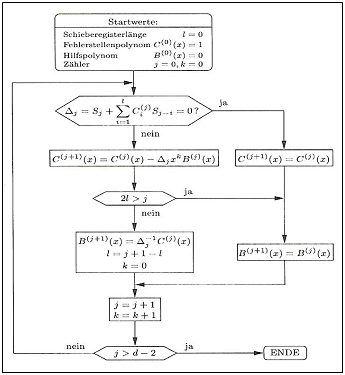
| − | [[File: P_ID2580__KC_A_2_14_v1.png|right|frame|Grafik aus [Bos98]: <br>'''(1)''' | + | [[File: P_ID2580__KC_A_2_14_v1.png|right|frame|Grafik aus [Bos98]: <br>'''(1)''' Fast decoding algorithm for RS codes. <br>'''(2)''' It is therefore not the Petersen algorithm!]] |
| − | + | In the chapter [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding|"Error correction after Reed-Solomon coding"]] the decoding of Reed–Solomon codes with the <i>Petersen algorithm</i> was treated. | |
| − | * | + | * Its advantage is that the individual steps are traceable. |
| − | * | + | * Very much of disadvantage is however the immensely high decoding expenditure. |
| − | + | Already since the invention of Reed–Solomon coding in 1960, many scientists and engineers were engaged in the development of algorithms for Reed–Solomon decoding as fast as possible, and even today <i>Algebraic Decoding</i> is still a highly topical field of research. | |
| − | In | + | In this exercise, some related concepts will be explained. A detailed explanation of these procedures has been omitted in $\rm LNTwww $ . |
| Line 15: | Line 15: | ||
| − | + | Hints: | |
* Die Aufgabe gehört zum Kapitel [[Channel_Coding/Fehlerkorrektur_nach_Reed%E2%80%93Solomon%E2%80%93Codierung| Fehlerkorrektur nach Reed–Solomon–Codierung]]. | * Die Aufgabe gehört zum Kapitel [[Channel_Coding/Fehlerkorrektur_nach_Reed%E2%80%93Solomon%E2%80%93Codierung| Fehlerkorrektur nach Reed–Solomon–Codierung]]. | ||
* Die Grafik zeigt das Flussdiagramm eines der bekanntesten Verfahren zur Decodierung von Reed–Solomon–Codes. Um welchen Algorithmus es sich dabei handelt, wird in der Musterlösung zu dieser Aufgabe genannt. | * Die Grafik zeigt das Flussdiagramm eines der bekanntesten Verfahren zur Decodierung von Reed–Solomon–Codes. Um welchen Algorithmus es sich dabei handelt, wird in der Musterlösung zu dieser Aufgabe genannt. | ||
| Line 22: | Line 22: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {For which codes is syndrome decoding used? For |
|type="[]"} | |type="[]"} | ||
| − | + | + | + binary block codes, |
| − | - Reed–Solomon | + | - Reed–Solomon codes, |
| − | - | + | - convolutional codes. |
| − | { | + | {What is most complex in the Petersen algorithm? |
|type="()"} | |type="()"} | ||
| − | - | + | - Checking if there are (one or more) errors at all, |
| − | + | + | + the localization of the errors, |
| − | - | + | - the determination of the error value. |
| − | { | + | {Which terms refer to Reed–Solomon decoding? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The Berlekamp–Massey algorithm, |
| − | - | + | - the BCJR algorithm, |
| − | + | + | + the Euclidean algorithm, |
| − | + | + | + frequency domain methods based on the DFT, |
| − | - | + | - the Viterbi algorithm. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is the <u>answer 1</u>: |
| − | * | + | *In principle, a syndrome decoder would also be possible with RS codes, but with the large codeword lengths $n$ common here, extremely long decoding times would result. |
| − | * | + | *For convolutional codes (these work serially) syndrome decoding makes no sense at all. |
| − | '''(2)''' | + | '''(2)''' As can be seen from the discussion in the theory section, error localization involves by far the greatest effort ⇒ <u>Answer 2</u>. |
| − | '''(3)''' | + | '''(3)''' Correct <u>answers 1, 3, and 4</u>: |
| − | * | + | *These procedures are summarized on the [[Channel_Coding/Error_Correction_According_to_Reed-Solomon_Coding#Fast_Reed-Solomon_decoding| "Fast Reed–Solomon decoding"]] page. |
| − | * | + | *The BCJR– and Viterbi algorithms, on the other hand, refer to [[Channel_Coding/Decoding_of_Convolutional_Codes|"Decoding of convolutional codes"]]. |
| − | * | + | *The graphic on the information page shows the Berlekamp–Massey algorithm (BMA). |
| − | * | + | *The explanation of this figure can be found in the reference book [Bos98]: "Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998" from page 73. |
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 19:02, 12 September 2022
In the chapter "Error correction after Reed-Solomon coding" the decoding of Reed–Solomon codes with the Petersen algorithm was treated.
- Its advantage is that the individual steps are traceable.
- Very much of disadvantage is however the immensely high decoding expenditure.
Already since the invention of Reed–Solomon coding in 1960, many scientists and engineers were engaged in the development of algorithms for Reed–Solomon decoding as fast as possible, and even today Algebraic Decoding is still a highly topical field of research.
In this exercise, some related concepts will be explained. A detailed explanation of these procedures has been omitted in $\rm LNTwww $ .
Hints:
- Die Aufgabe gehört zum Kapitel Fehlerkorrektur nach Reed–Solomon–Codierung.
- Die Grafik zeigt das Flussdiagramm eines der bekanntesten Verfahren zur Decodierung von Reed–Solomon–Codes. Um welchen Algorithmus es sich dabei handelt, wird in der Musterlösung zu dieser Aufgabe genannt.
- Die Grafik wurde dem Fachbuch [Bos98]: "Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998" entnommen. Wir danken dem Autor Martin Bossert für die Erlaubnis, die Grafik verwenden zu dürfen.
Questions
Solution
(1) Correct is the answer 1:
- In principle, a syndrome decoder would also be possible with RS codes, but with the large codeword lengths $n$ common here, extremely long decoding times would result.
- For convolutional codes (these work serially) syndrome decoding makes no sense at all.
(2) As can be seen from the discussion in the theory section, error localization involves by far the greatest effort ⇒ Answer 2.
(3) Correct answers 1, 3, and 4:
- These procedures are summarized on the "Fast Reed–Solomon decoding" page.
- The BCJR– and Viterbi algorithms, on the other hand, refer to "Decoding of convolutional codes".
- The graphic on the information page shows the Berlekamp–Massey algorithm (BMA).
- The explanation of this figure can be found in the reference book [Bos98]: "Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998" from page 73.