Difference between revisions of "Aufgaben:Exercise 3.09: Basics of the Viterbi Algorithm"
| Line 1: | Line 1: | ||
| − | {{quiz-Header|Buchseite= | + | {{quiz-Header|Buchseite=Channel_Coding/Decoding_of_Convolutional_Codes}} |
| − | [[File:P_ID2659__KC_A_3_8.png|right|frame| | + | [[File:P_ID2659__KC_A_3_8.png|right|frame|Trellis to be analyzed]] |
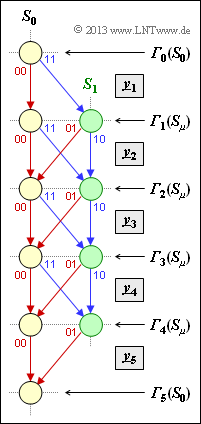
| − | + | The graph shows a trellis diagram and simultaneously defines the branch metrics ${\it \Gamma}_i(S_0)$ and ${\it \Gamma}_i(S_1)$ at times $i = 0$ to $i = 5$. | |
| − | + | From this trellis can be read, for example: | |
| − | * | + | * the code rate $R$, |
| − | * | + | * the memory $m$, |
| − | * | + | * the free distance $d_{\rm F}$, |
| − | * | + | * the information sequence length $L$, |
| − | * | + | * the sequence length $L\hspace{0.05cm}'$ including the termination. |
| − | In | + | In the exercise it is further necessary to clarify: |
| − | * | + | * the meaning of the final value ${\it \Gamma}_5(S_0)$, |
| − | * | + | * effects of one and two transmission errors, respectively. |
| Line 23: | Line 23: | ||
| − | + | Hint: | |
| − | * | + | * This exercise belongs to the chapter [[Channel_Coding/Decoding_of_Convolutional_Codes| "Decoding of Convolutional Codes"]]. |
| Line 33: | Line 33: | ||
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which of the following statements are confirmed by the trellis? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + It is a rate 1/2 convolutional code. |
| − | - | + | - The memory of the code is $m = 2$. |
| − | + | + | + The convolutional code is terminated. |
| − | - | + | - The length of the information sequence is $L = 5$. |
| − | { | + | {Specify the free distance $d_{\rm F}$ of the convolutional code. |
|type="{}"} | |type="{}"} | ||
$d_{\rm F} \ = \ ${ 3 3% } | $d_{\rm F} \ = \ ${ 3 3% } | ||
| − | { | + | {What statements does the final value ${\it \Gamma}_5(S_0) = 0$ of the branch metric allow? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - No transmission error has occurred. |
| − | - | + | - The decoding result $\underline{v}$ is certainly correct $($equal $\underline{u})$. |
| − | + | + | + The decoding result minimizes the probability ${\rm Pr}(\underline{v} ≠ \underline{u})$. |
| − | { | + | {Which statements are true <u>in the case of a single</u> transmission error? |
|type="[]"} | |type="[]"} | ||
| − | + | + | + The final branch metric is ${\it \Gamma}_5(S_0) = 1$. |
| − | + | + | + The decoding result $\underline{v}$ is certainly correct $($equal $\underline{u})$. |
| − | + | + | + The decoding result minimizes the probability ${\rm Pr}(\underline{v} ≠ \underline{u})$. |
| − | { | + | {Which statements are true <u>in the case of two</u> transmission errors? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The final branch metric is ${\it \Gamma}_5(S_0) = 2$. |
| − | - | + | - The decoding result $\underline{v}$ is certainly correct $($equal $\underline{u})$. |
| − | - | + | - The decoding result $\underline{v}$ is certainly false $($unequal $\underline{u})$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct are the <u>solutions 1 and 3</u>: |
| − | * | + | *There are $2^{k \cdot m} = 2$ states here. It follows that $k = 1$ and $m = 1$. |
| − | * | + | *Per coding step, $n = 2$ code bits are output ⇒ $R = 1/2$. |
| − | * | + | *The information sequence length is $L = 4$. |
| − | * | + | *Only by one (since $m = 1$) additional termination bit one arrives at the total length $L' = 5$. |
| − | '''(2)''' | + | '''(2)''' The free distance $d_{\rm F}$ is defined as the number of codebits in which two sequences $\underline{x}$ and $\underline{x'}$ differ. We choose the zero sequence as the reference sequence: |
:$$\underline{x}\hspace{0.03cm}' = \underline{0} = \big (00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.05cm},$$ | :$$\underline{x}\hspace{0.03cm}' = \underline{0} = \big (00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.05cm},$$ | ||
| − | + | expressed with the sequence of states: $S_0 → S_0 → S_0 → S_0 → \ \text{...} \ $ | |
| − | * | + | *One of the sequences $\underline{x} ≠ \underline{0}$, which differs from $\underline{0}$ only in the minimum number of codebits, follows the path $S_0 → S_1 → S_0 → S_0 → \text{...} \ $: |
:$$\underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) | :$$\underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} d_{\rm F}\hspace{0.1cm}\underline{ = 3} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} d_{\rm F}\hspace{0.1cm}\underline{ = 3} | ||
| Line 86: | Line 86: | ||
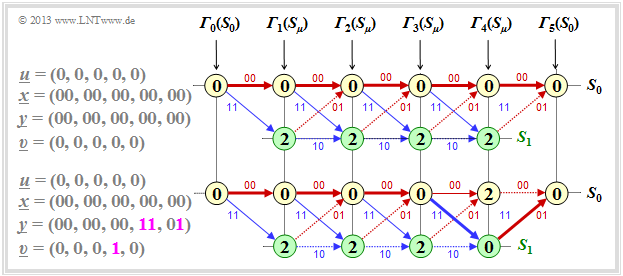
| − | '''(3)''' | + | '''(3)''' Only <u>proposition 3</u> is correct here, because the event "No transmission error" is much more likely than three errors at exactly specified positions. Consider the following graphic: |
| − | [[File:P_ID2660__KC_A_3_9c.png|center|frame|Trellis | + | [[File:P_ID2660__KC_A_3_9c.png|center|frame|Trellis without error/with three transmission errors]] |
| − | * | + | *If the zero sequence is sent and this is also received, the Viterbi decoding can be illustrated by the upper trellis. |
| − | * | + | *The final value of the branch metric is ${\it \Gamma}_5(S_0) = 0$, and the Viterbi decoder decides correctly with certainty: $\underline{z} = \underline{x} ⇒ \underline{v} = \underline{u}$. |
| − | * | + | *For the lower trellis, we also assume $\underline{u} = (0, \, 0, \, 0, \, 0 \, 0) ⇒ \underline{x} = (00, \, 00, \, 00, \, 00, \, 00)$. However, $\underline{y} = (00, \, 00, \, 00, \, 11, \, 01)$ is now received. Nevertheless, ${\it \Gamma}_5(S_0) = 0$ holds. The example proves that the first two statements are false. |
| + | '''(4)''' Correct are <u>all answers</u>: | ||
| + | *If it is known for sure that only one transmission error occurred, for a convolutional code with free distance $d_{\rm F} = 3$ the Viterbi algorithm works perfectly, no matter at which position the error occurred. | ||
| − | |||
| − | |||
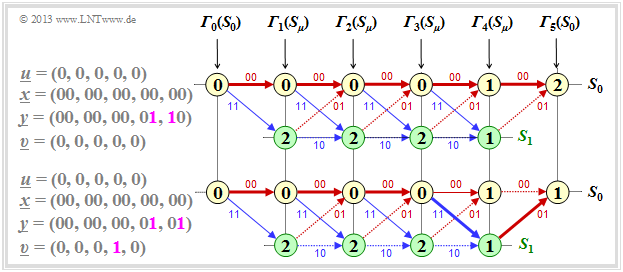
| + | '''(5)''' <u> None of the proposed solutions</u> is correct, as can be seen from the examples below. | ||
| − | + | [[File:P_ID2661__KC_A_3_9e.png|center|frame|Trellis with two transmission errors]] | |
| − | |||
| − | [[File:P_ID2661__KC_A_3_9e.png|center|frame|Trellis | ||
{{ML-Fuß}} | {{ML-Fuß}} | ||
Revision as of 21:47, 17 October 2022
The graph shows a trellis diagram and simultaneously defines the branch metrics ${\it \Gamma}_i(S_0)$ and ${\it \Gamma}_i(S_1)$ at times $i = 0$ to $i = 5$.
From this trellis can be read, for example:
- the code rate $R$,
- the memory $m$,
- the free distance $d_{\rm F}$,
- the information sequence length $L$,
- the sequence length $L\hspace{0.05cm}'$ including the termination.
In the exercise it is further necessary to clarify:
- the meaning of the final value ${\it \Gamma}_5(S_0)$,
- effects of one and two transmission errors, respectively.
Hint:
- This exercise belongs to the chapter "Decoding of Convolutional Codes".
Questions
Solution
- There are $2^{k \cdot m} = 2$ states here. It follows that $k = 1$ and $m = 1$.
- Per coding step, $n = 2$ code bits are output ⇒ $R = 1/2$.
- The information sequence length is $L = 4$.
- Only by one (since $m = 1$) additional termination bit one arrives at the total length $L' = 5$.
(2) The free distance $d_{\rm F}$ is defined as the number of codebits in which two sequences $\underline{x}$ and $\underline{x'}$ differ. We choose the zero sequence as the reference sequence:
- $$\underline{x}\hspace{0.03cm}' = \underline{0} = \big (00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.05cm},$$
expressed with the sequence of states: $S_0 → S_0 → S_0 → S_0 → \ \text{...} \ $
- One of the sequences $\underline{x} ≠ \underline{0}$, which differs from $\underline{0}$ only in the minimum number of codebits, follows the path $S_0 → S_1 → S_0 → S_0 → \text{...} \ $:
- $$\underline{x} = \big (11\hspace{0.05cm}, 01\hspace{0.05cm}, 00\hspace{0.05cm}, 00\hspace{0.05cm}, ... \hspace{0.1cm} \big ) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} d_{\rm F}\hspace{0.1cm}\underline{ = 3} \hspace{0.05cm}.$$
(3) Only proposition 3 is correct here, because the event "No transmission error" is much more likely than three errors at exactly specified positions. Consider the following graphic:
- If the zero sequence is sent and this is also received, the Viterbi decoding can be illustrated by the upper trellis.
- The final value of the branch metric is ${\it \Gamma}_5(S_0) = 0$, and the Viterbi decoder decides correctly with certainty: $\underline{z} = \underline{x} ⇒ \underline{v} = \underline{u}$.
- For the lower trellis, we also assume $\underline{u} = (0, \, 0, \, 0, \, 0 \, 0) ⇒ \underline{x} = (00, \, 00, \, 00, \, 00, \, 00)$. However, $\underline{y} = (00, \, 00, \, 00, \, 11, \, 01)$ is now received. Nevertheless, ${\it \Gamma}_5(S_0) = 0$ holds. The example proves that the first two statements are false.
(4) Correct are all answers:
- If it is known for sure that only one transmission error occurred, for a convolutional code with free distance $d_{\rm F} = 3$ the Viterbi algorithm works perfectly, no matter at which position the error occurred.
(5) None of the proposed solutions is correct, as can be seen from the examples below.