Difference between revisions of "Aufgaben:Exercise 4.3: Iterative Decoding at the BSC"
| Line 2: | Line 2: | ||
[[File:P_ID2987__KC_A_4_3_v1.png|right|frame|BSC model and possible received values]] | [[File:P_ID2987__KC_A_4_3_v1.png|right|frame|BSC model and possible received values]] | ||
| − | + | We consider two codes in this exercise: | |
| − | * | + | * the Single Parity–Code ⇒ [[Channel_Coding/Examples_of_Binary_Block_Codes#Single_Parity-check_Codes| $\text{"SPC (3, 2, 2)"}$]]: |
:$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} | :$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} | ||
(0, 1, 1), \hspace{0.1cm} | (0, 1, 1), \hspace{0.1cm} | ||
| Line 9: | Line 9: | ||
(1, 1, 0) \hspace{0.05cm} \big ) | (1, 1, 0) \hspace{0.05cm} \big ) | ||
\hspace{0.05cm}, $$ | \hspace{0.05cm}, $$ | ||
| − | * | + | * the repetition code ⇒ [[Channel_Coding/Examples_of_Binary_Block_Codes#Repetition_Codes| $\text{"RC (3, 1, 3)"}$]]: |
:$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} | :$$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} | ||
(1, 1, 1) \hspace{0.05cm} \big ) | (1, 1, 1) \hspace{0.05cm} \big ) | ||
| Line 15: | Line 15: | ||
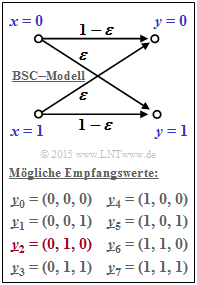
| − | + | The channel is described at bit level by the [[Digital_Signal_Transmission/Binary_Symmetric_Channel|"BSC–model"]] . According to the graphic, the following applies: | |
:$${\rm Pr}(y_i \ne x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}\varepsilon = 0.269\hspace{0.05cm},$$ | :$${\rm Pr}(y_i \ne x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}\varepsilon = 0.269\hspace{0.05cm},$$ | ||
:$${\rm Pr}(y_i = x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1-\varepsilon = 0.731\hspace{0.05cm}.$$ | :$${\rm Pr}(y_i = x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1-\varepsilon = 0.731\hspace{0.05cm}.$$ | ||
| − | + | Here, $\varepsilon$ denotes the corruption probability of the BSC model. | |
| − | + | Except for the last subtask, the following received value is always assumed: | |
:$$\underline{y} = (0, 1, 0) =\underline{y}_2 | :$$\underline{y} = (0, 1, 0) =\underline{y}_2 | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | + | The here chosen indexing of all possible received vectors can be taken from the graphic. | |
| − | * | + | *The most considered vector $\underline{y}_2$ is highlighted in red here. |
| − | * | + | *For the subtask '''(6)''' then applies: |
:$$\underline{y} = (1, 1, 0) =\underline{y}_6 | :$$\underline{y} = (1, 1, 0) =\underline{y}_6 | ||
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
| − | + | For decoding purposes, the exercise will examine: | |
| − | * | + | * the [[Channel_Coding/Decoding_of_Linear_Block_Codes#Generalization_of_syndrome_coding|"Syndrome Decoding"]], which follows the concept <i>hard decision maximum likelihood detection</i> (HD ML) for the codes under consideration. <br>(soft values are not available at the BSC), |
| − | * | + | * the symbol-wise [[Channel_Coding/Soft-in_Soft-Out_Decoder#Symbol-wise_soft-in_soft-out_decoding|"Soft–in Soft–out Decoding"]] (SISO) according to this section. |
| Line 44: | Line 44: | ||
| − | + | Hints: | |
| − | * | + | * This exercise refers to the chapter [[Channel_Coding/Soft-in_Soft-Out_Decoder| "Soft–in Soft–out Decoder"]]. |
| − | * | + | * Reference is made in particular to the pages |
| − | ::[[Channel_Coding/Soft-in_Soft-Out_Decoder#Symbol-wise_soft-in_soft-out_decoding|" | + | ::[[Channel_Coding/Soft-in_Soft-Out_Decoder#Symbol-wise_soft-in_soft-out_decoding|"Symbol-wise Soft–in Soft–out_Decoding"]], as well as |
| − | ::[[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|''Binary Symmetric Channel'']] | + | ::[[Channel_Coding/Channel_Models_and_Decision_Structures#Binary_Symmetric_Channel_.E2.80.93_BSC|''Binary Symmetric Channel'']] |
| − | * | + | * The codeword selected by the decoder is denoted by $\underline{z}$ in the questions. |
| − | === | + | ===Questions=== |
<quiz display=simple> | <quiz display=simple> | ||
| − | { | + | {Which statements are valid for decoding the $\text{SPC (3, 2, 2)}$? |
|type="()"} | |type="()"} | ||
| − | - | + | - The HD syndrome decoding yields the result $\underline{z} = (0, \, 1, \, 0)$. |
| − | - | + | - The HD syndrome decoding returns the result $\underline{z} = (0, \, 0, \, 0)$. |
| − | + | + | + The HD syndrome decoding fails here. |
| − | { | + | {Which statements are valid for the $\text{ RC (3, 1, 3)}$? |
|type="()"} | |type="()"} | ||
| − | - | + | - The HD syndrome decoding returns the result $\underline{z} = (0, \, 1, \, 0)$. |
| − | + | + | + The HD syndrome decoding returns the result $\underline{z} = (0, \, 0, \, 0)$. |
| − | - | + | - The HD syndrome decoding fails here. |
| − | { | + | {How certain is this decision if we define certainty $S$ as the quotient of the probabilities for a correct or incorrect decision? <br>Set the corruption probability of the BSC model to $\varepsilon = 26.9\%$. |
|type="{}"} | |type="{}"} | ||
$S \ = \ ${ 2.717 3% } | $S \ = \ ${ 2.717 3% } | ||
$\hspace{0.75cm} \ln {(S)} \ = \ ${ 1 3% } | $\hspace{0.75cm} \ln {(S)} \ = \ ${ 1 3% } | ||
| − | { | + | {What are the intrinsic LLR for the iterative symbol-wise decoding of the $\text{RC (3, 1)}$ received word $\underline{y}_2 = (0, \, 1, \, 0)$? |
|type="{}"} | |type="{}"} | ||
$L_{\rm K}(1) \ = \ ${ 1 3% } | $L_{\rm K}(1) \ = \ ${ 1 3% } | ||
| Line 79: | Line 79: | ||
$L_{\rm K}(3) \ = \ ${ 1 3% } | $L_{\rm K}(3) \ = \ ${ 1 3% } | ||
| − | { | + | {Which statements are true for decoding the received word $\underline{y}_2 = (0, \, 1, \, 0)$ ? Continue to assume the $\text{RC (3, 1, 3)}$. |
|type="[]"} | |type="[]"} | ||
| − | + | + | + From the first iteration all signs of $L_{\rm APP}(i)$ are positive. |
| − | + | + | + Already after the second iteration ${\rm Pr}(\underline{x}_0\hspace{0.05cm} |\hspace{0.05cm} \underline{y}_2)$ is greater than $99\%$. |
| − | + | + | + With each iteration the absolute values $L_{\rm APP}(i)$ become larger. |
| − | { | + | {Which statements are true for decoding the received word $\underline{y}_6 = (1, 1, 0)$ when $\underline{x}_0 = (0, 0, 0)$ was sent? |
|type="[]"} | |type="[]"} | ||
| − | - | + | - The iterative decoder decides correctly. |
| − | + | + | + The iterative decoder decides wrong. |
| − | + | + | + The "reliability" for "$\underline{y}_6 \Rightarrow \underline{x}_0$" increases with increasing $I$. |
</quiz> | </quiz> | ||
| − | === | + | ===Solution=== |
{{ML-Kopf}} | {{ML-Kopf}} | ||
| − | '''(1)''' | + | '''(1)''' Correct is the <u>proposed solution 3</u>: |
| − | * | + | *The received word $\underline{y}_2 = (0, 1, 0)$ is not a valid codeword of the <i>single parity–check code</i> SPC (3, 2). Thus, the first statement is false. |
| − | * | + | *In addition, since the SPC (3, 2) has only the minimum distance $d_{\rm min} = 2$, no error can be corrected. |
| − | '''(2)''' | + | '''(2)''' Correct is the <u>proposed solution 2</u>: |
| − | * | + | *The possible codewords at RP (3, 1) are $\underline{x}_0 = (0, 0, 0)$ and $\underline{x}_1 = (1, 1, 1)$. |
| − | * | + | *The minimum distance of this code is $d_{\rm min} = 3$, so $t = (d_{\rm min} \, - 1)/2 = 1$ error can be corrected. |
| − | * | + | *In addition to $\underline{y}_0 = (0, 0, 0)$, $\underline{y}_1 = (0, 0, 1), \ \underline{y}_2 = (0, 1, 0)$, and $\underline{y}_4 = (1, 0, 0)$ are also assigned to the decoding result $\underline{x}_0 = (0, 0, 0)$. |
| − | '''(3)''' | + | '''(3)''' According to the BSC model, the conditional probability is that $\underline{y}_2 = (0, 1, 0)$ is received, given that $\underline{x}_0 = (0, 0, 0)$ was sent: |
:$${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) = (1-\varepsilon)^2 \cdot \varepsilon\hspace{0.05cm}.$$ | :$${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) = (1-\varepsilon)^2 \cdot \varepsilon\hspace{0.05cm}.$$ | ||
| − | * | + | *The first term $(1 \, –\varepsilon)^2$ indicates the probability that the first and the third bit were transmitted correctly and $\varepsilon$ considers the corruption probability for the second bit. |
| − | * | + | *Correspondingly, for the second possible code word $\underline{x}_1 = (1, 1, 1)$: |
:$${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) = \varepsilon^2 \cdot (1-\varepsilon) \hspace{0.05cm}.$$ | :$${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) = \varepsilon^2 \cdot (1-\varepsilon) \hspace{0.05cm}.$$ | ||
| − | * | + | *According to Bayes' theorem, the inference probabilities are then: |
:$${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_0)} | :$${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_0)} | ||
{{\rm Pr}(\underline{y} = \underline{y}_2)} \hspace{0.05cm},$$ | {{\rm Pr}(\underline{y} = \underline{y}_2)} \hspace{0.05cm},$$ | ||
| Line 121: | Line 121: | ||
{{\rm Pr}(\underline{y} = \underline{y}_2)} $$ | {{\rm Pr}(\underline{y} = \underline{y}_2)} $$ | ||
:$$\Rightarrow \hspace{0.3cm} S = \frac{{\rm Pr(richtige \hspace{0.15cm}Entscheidung)}} | :$$\Rightarrow \hspace{0.3cm} S = \frac{{\rm Pr(richtige \hspace{0.15cm}Entscheidung)}} | ||
| − | {{\rm Pr( | + | {{\rm Pr(wrong \hspace{0.15cm}decision) }} = \frac{(1-\varepsilon)^2 \cdot \varepsilon}{\varepsilon^2 \cdot (1-\varepsilon)}= \frac{(1-\varepsilon)}{\varepsilon}\hspace{0.05cm}.$$ |
| − | * | + | *With $\varepsilon = 0.269$ we get the following numerical values: |
:$$S = {0.731}/{0.269}\hspace{0.15cm}\underline {= 2.717}\hspace{0.3cm}\Rightarrow | :$$S = {0.731}/{0.269}\hspace{0.15cm}\underline {= 2.717}\hspace{0.3cm}\Rightarrow | ||
\hspace{0.3cm}{\rm ln}\hspace{0.15cm}(S)\hspace{0.15cm} \underline {= 1}\hspace{0.05cm}.$$ | \hspace{0.3cm}{\rm ln}\hspace{0.15cm}(S)\hspace{0.15cm} \underline {= 1}\hspace{0.05cm}.$$ | ||
| Line 129: | Line 129: | ||
| − | '''(4)''' | + | '''(4)''' The sign of the channel LLR $L_{\rm K}(i)$ is positive if $y_i = 0$, and negative for $y_i = 1$. |
| − | * | + | *The absolute value indicates the reliability of $y_i$. In the BSC model, $|L_{\rm K}(i)| = \ln {(1 \, – \varepsilon)/\varepsilon} = 1$ for all $i$. Thus: |
| − | [[File:P_ID2988__KC_A_4_3e_v1.png|rightr|frame| Iterative | + | [[File:P_ID2988__KC_A_4_3e_v1.png|rightr|frame| Iterative decoding of $(+1, -1, +1)$]] |
:$$\underline {L_{\rm K}}(1)\hspace{0.15cm} \underline {= +1}\hspace{0.05cm},\hspace{0.5cm} | :$$\underline {L_{\rm K}}(1)\hspace{0.15cm} \underline {= +1}\hspace{0.05cm},\hspace{0.5cm} | ||
\underline {L_{\rm K}}(2)\hspace{0.15cm} \underline {= -1}\hspace{0.05cm},\hspace{0.5cm} | \underline {L_{\rm K}}(2)\hspace{0.15cm} \underline {= -1}\hspace{0.05cm},\hspace{0.5cm} | ||
| Line 138: | Line 138: | ||
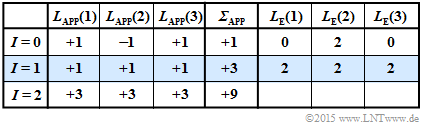
| − | '''(5)''' | + | '''(5)''' The adjacent table illustrates the iterative symbol-wise decoding starting from $\underline{y}_2 = (0, \, 1, \, 0)$. |
<br clear=all> | <br clear=all> | ||
| − | + | These results can be interpreted as follows: | |
| − | * | + | * The preassignment (iteration $I = 0$) happens according to $\underline{L}_{\rm APP} = \underline{L}_{\rm K}$. A hard decision ⇒ "$\sign {\underline{L}_{\rm APP}(i)}$" would lead to the decoding result $(0, \, 1, \, 0)$. The reliability of this obviously incorrect result is given as $|{\it \Sigma}| = 1$. This value agrees with the "$\ln (S)$" calculated in subtasks (3). |
| − | * | + | * After the first iteration $(I = 1)$ all a posteriori LLRs are $L_{\rm APP}(i) = +1$. A hard decision here would yield the (expected) correct result $\underline{x}_{\rm APP} = (0, \, 0, \, 0)$. The probability that this outcome is correct is quantified by $|{\it \Sigma}_{\rm APP}| = 3$: |
:$${\rm ln}\hspace{0.25cm}\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = 3 | :$${\rm ln}\hspace{0.25cm}\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = 3 | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
| Line 148: | Line 148: | ||
:$$\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {20}/{21} | :$$\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {20}/{21} | ||
{\approx 95.39\%}\hspace{0.05cm}.$$ | {\approx 95.39\%}\hspace{0.05cm}.$$ | ||
| − | * | + | * The second iteration confirms the decoding result of the first iteration. The reliability is even quantified here with "$9$". This value can be interpreted as follows: |
:$$\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = {\rm e}^9 | :$$\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = {\rm e}^9 | ||
\hspace{0.3cm}\Rightarrow \hspace{0.3cm} | \hspace{0.3cm}\Rightarrow \hspace{0.3cm} | ||
{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {{\rm e}^9}/{({\rm e}^9+1)} | {\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {{\rm e}^9}/{({\rm e}^9+1)} | ||
\approx 99.99\% \hspace{0.05cm}.$$ | \approx 99.99\% \hspace{0.05cm}.$$ | ||
| + | *With each further iteration the reliability value and thus the probability ${\rm Pr}(\underline{x}_0 | \underline{y}_2)$ increases drastically ⇒ <u>All proposed solutions</u> are correct. | ||
| − | |||
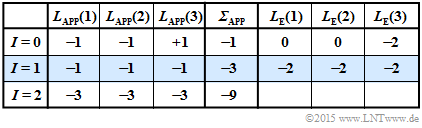
| + | [[File:P_ID2991__KC_A_4_3f_v1.png|right|frame|Iterative decoding of $(–1, –1, +1)$]] | ||
| + | '''(6)''' Correct are <u>the proposed solutions 2 and 3</u>: | ||
| + | *For the received vector $\underline{y}_6 = (1, \, 1, \, 0)$, the second table applies. | ||
| − | + | *The decoder now decides for the sequence $\underline{x}_1 = (1, \, 1, \, 1)$. | |
| − | + | *The case "$\underline{y}_3 = (1, \, 1, \, 0)$ received under the condition $\underline{x}_1 = (1, \, 1, \, 1)$ sent" would correspond exactly to the constellation "$\underline{y}_2 = (1, \, 0, \, 1)$ received and $\underline{x}_0 = (0, \, 0, \, 0)$ sent" considered in the last subtask. | |
| − | * | + | *But since $\underline{x}_0 = (0, \, 0, \, 0)$ was sent, there are now two bit errors with the following consequence: |
| − | + | :* The iterative decoder decides incorrectly. | |
| − | + | :* With each further iteration the wrong decision is declared as more reliable. | |
| − | * | ||
| − | * | ||
| − | :* | ||
| − | :* | ||
Revision as of 18:04, 27 October 2022
We consider two codes in this exercise:
- the Single Parity–Code ⇒ $\text{"SPC (3, 2, 2)"}$:
- $$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} (0, 1, 1), \hspace{0.1cm} (1, 0, 1), \hspace{0.1cm} (1, 1, 0) \hspace{0.05cm} \big ) \hspace{0.05cm}, $$
- the repetition code ⇒ $\text{"RC (3, 1, 3)"}$:
- $$\underline{x} = \big (\hspace{0.05cm}(0, 0, 0), \hspace{0.1cm} (1, 1, 1) \hspace{0.05cm} \big ) \hspace{0.05cm}.$$
The channel is described at bit level by the "BSC–model" . According to the graphic, the following applies:
- $${\rm Pr}(y_i \ne x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}\varepsilon = 0.269\hspace{0.05cm},$$
- $${\rm Pr}(y_i = x_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1-\varepsilon = 0.731\hspace{0.05cm}.$$
Here, $\varepsilon$ denotes the corruption probability of the BSC model.
Except for the last subtask, the following received value is always assumed:
- $$\underline{y} = (0, 1, 0) =\underline{y}_2 \hspace{0.05cm}. $$
The here chosen indexing of all possible received vectors can be taken from the graphic.
- The most considered vector $\underline{y}_2$ is highlighted in red here.
- For the subtask (6) then applies:
- $$\underline{y} = (1, 1, 0) =\underline{y}_6 \hspace{0.05cm}. $$
For decoding purposes, the exercise will examine:
- the "Syndrome Decoding", which follows the concept hard decision maximum likelihood detection (HD ML) for the codes under consideration.
(soft values are not available at the BSC), - the symbol-wise "Soft–in Soft–out Decoding" (SISO) according to this section.
Hints:
- This exercise refers to the chapter "Soft–in Soft–out Decoder".
- Reference is made in particular to the pages
- The codeword selected by the decoder is denoted by $\underline{z}$ in the questions.
Questions
Solution
- The received word $\underline{y}_2 = (0, 1, 0)$ is not a valid codeword of the single parity–check code SPC (3, 2). Thus, the first statement is false.
- In addition, since the SPC (3, 2) has only the minimum distance $d_{\rm min} = 2$, no error can be corrected.
(2) Correct is the proposed solution 2:
- The possible codewords at RP (3, 1) are $\underline{x}_0 = (0, 0, 0)$ and $\underline{x}_1 = (1, 1, 1)$.
- The minimum distance of this code is $d_{\rm min} = 3$, so $t = (d_{\rm min} \, - 1)/2 = 1$ error can be corrected.
- In addition to $\underline{y}_0 = (0, 0, 0)$, $\underline{y}_1 = (0, 0, 1), \ \underline{y}_2 = (0, 1, 0)$, and $\underline{y}_4 = (1, 0, 0)$ are also assigned to the decoding result $\underline{x}_0 = (0, 0, 0)$.
(3) According to the BSC model, the conditional probability is that $\underline{y}_2 = (0, 1, 0)$ is received, given that $\underline{x}_0 = (0, 0, 0)$ was sent:
- $${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) = (1-\varepsilon)^2 \cdot \varepsilon\hspace{0.05cm}.$$
- The first term $(1 \, –\varepsilon)^2$ indicates the probability that the first and the third bit were transmitted correctly and $\varepsilon$ considers the corruption probability for the second bit.
- Correspondingly, for the second possible code word $\underline{x}_1 = (1, 1, 1)$:
- $${\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) = \varepsilon^2 \cdot (1-\varepsilon) \hspace{0.05cm}.$$
- According to Bayes' theorem, the inference probabilities are then:
- $${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_0 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_0)} {{\rm Pr}(\underline{y} = \underline{y}_2)} \hspace{0.05cm},$$
- $${\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_1 \hspace{0.1cm}| \hspace{0.1cm}\underline{y} = \underline{y}_2 ) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr}(\underline{y} = \underline{y}_2 \hspace{0.1cm}| \hspace{0.1cm}\underline{x} = \underline{x}_1 ) \cdot \frac{{\rm Pr}(\underline{x} = \underline{x}_1)} {{\rm Pr}(\underline{y} = \underline{y}_2)} $$
- $$\Rightarrow \hspace{0.3cm} S = \frac{{\rm Pr(richtige \hspace{0.15cm}Entscheidung)}} {{\rm Pr(wrong \hspace{0.15cm}decision) }} = \frac{(1-\varepsilon)^2 \cdot \varepsilon}{\varepsilon^2 \cdot (1-\varepsilon)}= \frac{(1-\varepsilon)}{\varepsilon}\hspace{0.05cm}.$$
- With $\varepsilon = 0.269$ we get the following numerical values:
- $$S = {0.731}/{0.269}\hspace{0.15cm}\underline {= 2.717}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm ln}\hspace{0.15cm}(S)\hspace{0.15cm} \underline {= 1}\hspace{0.05cm}.$$
(4) The sign of the channel LLR $L_{\rm K}(i)$ is positive if $y_i = 0$, and negative for $y_i = 1$.
- The absolute value indicates the reliability of $y_i$. In the BSC model, $|L_{\rm K}(i)| = \ln {(1 \, – \varepsilon)/\varepsilon} = 1$ for all $i$. Thus:
- $$\underline {L_{\rm K}}(1)\hspace{0.15cm} \underline {= +1}\hspace{0.05cm},\hspace{0.5cm} \underline {L_{\rm K}}(2)\hspace{0.15cm} \underline {= -1}\hspace{0.05cm},\hspace{0.5cm} \underline {L_{\rm K}}(3)\hspace{0.15cm} \underline {= +1}\hspace{0.05cm}.$$
(5) The adjacent table illustrates the iterative symbol-wise decoding starting from $\underline{y}_2 = (0, \, 1, \, 0)$.
These results can be interpreted as follows:
- The preassignment (iteration $I = 0$) happens according to $\underline{L}_{\rm APP} = \underline{L}_{\rm K}$. A hard decision ⇒ "$\sign {\underline{L}_{\rm APP}(i)}$" would lead to the decoding result $(0, \, 1, \, 0)$. The reliability of this obviously incorrect result is given as $|{\it \Sigma}| = 1$. This value agrees with the "$\ln (S)$" calculated in subtasks (3).
- After the first iteration $(I = 1)$ all a posteriori LLRs are $L_{\rm APP}(i) = +1$. A hard decision here would yield the (expected) correct result $\underline{x}_{\rm APP} = (0, \, 0, \, 0)$. The probability that this outcome is correct is quantified by $|{\it \Sigma}_{\rm APP}| = 3$:
- $${\rm ln}\hspace{0.25cm}\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = 3 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = {\rm e}^3 \approx 20$$
- $$\hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {20}/{21} {\approx 95.39\%}\hspace{0.05cm}.$$
- The second iteration confirms the decoding result of the first iteration. The reliability is even quantified here with "$9$". This value can be interpreted as follows:
- $$\frac{{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)}{1-{\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2)} = {\rm e}^9 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {\rm Pr}(\hspace{0.1cm}\underline{x} = \underline{x}_0 \hspace{0.1cm}| \hspace{0.1cm}\underline{y}=\underline{y}_2) = {{\rm e}^9}/{({\rm e}^9+1)} \approx 99.99\% \hspace{0.05cm}.$$
- With each further iteration the reliability value and thus the probability ${\rm Pr}(\underline{x}_0 | \underline{y}_2)$ increases drastically ⇒ All proposed solutions are correct.
(6) Correct are the proposed solutions 2 and 3:
- For the received vector $\underline{y}_6 = (1, \, 1, \, 0)$, the second table applies.
- The decoder now decides for the sequence $\underline{x}_1 = (1, \, 1, \, 1)$.
- The case "$\underline{y}_3 = (1, \, 1, \, 0)$ received under the condition $\underline{x}_1 = (1, \, 1, \, 1)$ sent" would correspond exactly to the constellation "$\underline{y}_2 = (1, \, 0, \, 1)$ received and $\underline{x}_0 = (0, \, 0, \, 0)$ sent" considered in the last subtask.
- But since $\underline{x}_0 = (0, \, 0, \, 0)$ was sent, there are now two bit errors with the following consequence:
- The iterative decoder decides incorrectly.
- With each further iteration the wrong decision is declared as more reliable.