Difference between revisions of "Aufgaben:Exercise 4.4Z: Supplement to Exercise 4.4"
| Line 2: | Line 2: | ||
[[File:P_ID2994__KC_Z_4_4_v3.png |right|frame|Hamming weights and sequence probabilities ]] | [[File:P_ID2994__KC_Z_4_4_v3.png |right|frame|Hamming weights and sequence probabilities ]] | ||
| − | + | The information theorist [https://en.wikipedia.org/wiki/Robert_G._Gallager "Robert G. Gallager"] already in 1963 dealt with the following problem: | |
| − | * | + | * Given a random vector $\underline{x} = (x_1, \, x_2, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , x_n)$ with $n$ binary elements $x_i ∈ \{0, \, 1\}$. |
| − | * | + | * Known are all probabilities $p_i = {\rm Pr}(x_i = 1)$ and $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$ with index $i = 1, \hspace{-0.04cm}\text{ ...} \hspace{0.08cm} ,\ n$. |
| − | * | + | * What we are looking for is the probability that the number of ones in this vector is even. |
| − | * | + | * Or expressed using the [[Channel_Coding/Objective_of_Channel_Coding#Important_definitions_for_block_coding|"Hamming weight"]]: What is the probability ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ even}]$? |
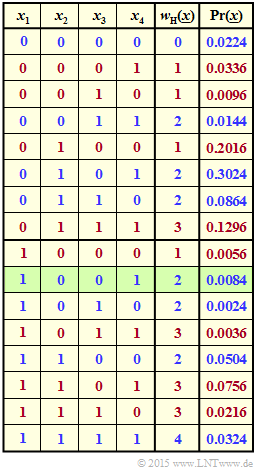
| − | + | The graph illustrates the task for the example $n = 4$ and $p_1 = 0.2$, $p_2 = 0.9$, $p_3 = 0.3$ and $p_4 = 0.6$. | |
| − | * | + | * For the row highlighted in green ⇒ $\underline{x} = (1, \, 0, \, 0, \, 1)$ holds $w_{\rm H}(\underline{x}) = 2$ and |
:$${\rm Pr}(\underline{x}) = p_1 \cdot q_2 \cdot q_3 \cdot p_4 = 0.0084.$$ | :$${\rm Pr}(\underline{x}) = p_1 \cdot q_2 \cdot q_3 \cdot p_4 = 0.0084.$$ | ||
| − | * | + | * Blue font means "$w_{\rm H}(\underline{x})$ is even". Red font stands for "$w_{\rm H}(\underline{x})$ is odd." |
| − | * | + | *The probability ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \is \even}]$ is the sum of the blue numbers in the last column. |
| − | * | + | *The sum of the red numbers gives ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ odd}] = 1 - {\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ even}]$. |
| Line 65: | Line 65: | ||
|type="{}"} | |type="{}"} | ||
${\rm Pr(blue) = Pr}\big [w_{\rm H}(\underline{x}) \ {\rm is \ even}\big ] \hspace{0.33cm} = \ ${ 0.5192 3% } | ${\rm Pr(blue) = Pr}\big [w_{\rm H}(\underline{x}) \ {\rm is \ even}\big ] \hspace{0.33cm} = \ ${ 0.5192 3% } | ||
| − | ${\rm Pr(red) = Pr}\big [w_{\rm H}(\underline{x}) \ {\rm is \ | + | ${\rm Pr(red) = Pr}\big [w_{\rm H}(\underline{x}) \ {\rm is \ odd}\big ] \hspace{0.1cm} = \ ${ 0.4808 3% } |
$\text{Quotient }Q = {\rm Pr(blau)/Pr(rot)} \hspace{0.4cm} = \ ${ 1.0799 3% } | $\text{Quotient }Q = {\rm Pr(blau)/Pr(rot)} \hspace{0.4cm} = \ ${ 1.0799 3% } | ||
| Line 113: | Line 113: | ||
The red rows provide the complementary event: | The red rows provide the complementary event: | ||
| − | :$$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} | + | :$$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}\right] = 0.024 + 0.504 + 0.014 + 0.054= 0.596 |
\hspace{0.05cm}.$$ | \hspace{0.05cm}.$$ | ||
| Line 129: | Line 129: | ||
From this can be calculated: | From this can be calculated: | ||
:$${\rm Pr}({\rm blue}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \pi = 0.5 + 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.5192}\hspace{0.05cm},$$ | :$${\rm Pr}({\rm blue}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \pi = 0.5 + 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.5192}\hspace{0.05cm},$$ | ||
| − | :$${\rm Pr}({\rm red}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} | + | :$${\rm Pr}({\rm red}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 - 0.5 \cdot \pi = 0.5 - 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.4808}\hspace{0.05cm}. $$ |
If you add up the blue and red probabilities on the information page, you get exactly the values calculated here. | If you add up the blue and red probabilities on the information page, you get exactly the values calculated here. | ||
For the quotient we get: | For the quotient we get: | ||
| − | :$$Q = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right]} { {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} | + | :$$Q = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right]} { {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}\right]} = \frac{0.5192}{0.4808}\hspace{0.15cm} \underline{= 1.0799} |
\hspace{0.05cm}. $$ | \hspace{0.05cm}. $$ | ||
'''(4)''' For the <i>single parity–check code</i>, the extrinsic $L$ value with respect to the $i$th bit was specified as follows: | '''(4)''' For the <i>single parity–check code</i>, the extrinsic $L$ value with respect to the $i$th bit was specified as follows: | ||
| − | :$$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} | + | :$$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} |
\hspace{0.05cm},$$ | \hspace{0.05cm},$$ | ||
Revision as of 23:06, 29 October 2022
The information theorist "Robert G. Gallager" already in 1963 dealt with the following problem:
- Given a random vector $\underline{x} = (x_1, \, x_2, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , x_n)$ with $n$ binary elements $x_i ∈ \{0, \, 1\}$.
- Known are all probabilities $p_i = {\rm Pr}(x_i = 1)$ and $q_i = {\rm Pr}(x_i = 0) = 1 - p_i$ with index $i = 1, \hspace{-0.04cm}\text{ ...} \hspace{0.08cm} ,\ n$.
- What we are looking for is the probability that the number of ones in this vector is even.
- Or expressed using the "Hamming weight": What is the probability ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ even}]$?
The graph illustrates the task for the example $n = 4$ and $p_1 = 0.2$, $p_2 = 0.9$, $p_3 = 0.3$ and $p_4 = 0.6$.
- For the row highlighted in green ⇒ $\underline{x} = (1, \, 0, \, 0, \, 1)$ holds $w_{\rm H}(\underline{x}) = 2$ and
- $${\rm Pr}(\underline{x}) = p_1 \cdot q_2 \cdot q_3 \cdot p_4 = 0.0084.$$
- Blue font means "$w_{\rm H}(\underline{x})$ is even". Red font stands for "$w_{\rm H}(\underline{x})$ is odd."
- The probability ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \is \even}]$ is the sum of the blue numbers in the last column.
- The sum of the red numbers gives ${\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ odd}] = 1 - {\rm Pr}[w_{\rm H}(\underline{x}) {\rm \ is \ even}]$.
Gallager hat das Problem in analytischer Weise gelöst:
- $$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \right ] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 + \pi]\hspace{0.05cm},$$
- $${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \right ] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1/2 \cdot [1 - \pi]\hspace{0.05cm}.$$
Hierbei ist die folgende Hilfsgröße verwendet:
- $$\pi = \prod\limits_{i =1}^{n} \hspace{0.25cm}(1-2p_i) \hspace{0.05cm}.$$
Die Gleichung wendet man zum Beispiel an, um die extrinsischen $L$–Werte eines Single Parity–check Codes zu berechnen.
Wie bereits in der "Aufgabe A4.4" dargelegt, lautet nämlich der extrinsische $L$–Wert mit dem Hamming–Gewicht $w_{\rm H}$ der verkürzten Folge $\underline{x}^{(-i)}$:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.$$
Hierbei ist berücksichtigt, dass man für $L_{\rm E}(i)$ nur die anderen Symbole $(j ≠ i)$ heranziehen darf:
- $$\underline{x}^{(-i)} = \big ( \hspace{0.03cm}x_1, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , \hspace{0.03cm} x_{i-1}, \hspace{0.43cm} x_{i+1}, \hspace{-0.04cm} \text{ ...} \hspace{0.08cm} , x_{n} \hspace{0.03cm} \big )\hspace{0.03cm}. $$
Hints:
- This exercise belongs to the chapter "Soft–in Soft–out Decoder".
- Reference is made in particular to the page "For calculating the extrinsic $L$–values".
- The exercise is intended as a supplement to "Exercise 4.4" .
Questions
Solution
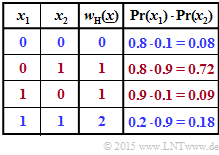
(1) According to the adjacent table applies:
- $${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.10cm}{\rm is \hspace{0.10cm} even}\right ] = {\rm Pr} \left [w_{\rm H} = 0 \right] + {\rm Pr} \left [w_{\rm H} = 2 \right] \hspace{0.05cm}. $$
With the probabilities
- $$p_1 = {\rm Pr} (x_1 = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.2\hspace{0.05cm},\hspace{0.3cm}q_1 = {\rm Pr} (x_1 = 0) = 0.8\hspace{0.05cm},$$
- $$p_2 = {\rm Pr} (x_2 = 1) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.9\hspace{0.05cm},\hspace{0.3cm}q_2 = {\rm Pr} (x_2 = 0) = 0.1$$
one obtains:
- $${\rm Pr} \left [w_{\rm H}(\underline{x}) = 0\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr} \left [(x_1 = 0)\cap (x_2 = 0) \right] = q_1 \cdot q_2 = 0.8 \cdot 0.1 = 0.08 \hspace{0.05cm},$$
- $${\rm Pr} \left [w_{\rm H}(\underline{x}) = 2\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Pr} \left [(x_1 = 1)\cap (x_2 = 1) \right] = p_1 \cdot p_2 = 0.2 \cdot 0.9 = 0.18$$
- $$\Rightarrow \hspace{0.3cm} {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] = 0.8 + 0.18 \hspace{0.15cm} \underline{= 0.26} \hspace{0.05cm}.$$
The Gallager's equation provides for the same set of parameters:
- $${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \prod\limits_{i =1}^{2} \hspace{0.25cm}(1-2\cdot p_i) = 0.5 + 0.5 \cdot (1 - 2 \cdot 0.2)\cdot (1 - 2 \cdot 0.9) = 0.26 \hspace{0.05cm}.$$
The equation given by Gallager 1963 was hereby verified for $n = 2$.
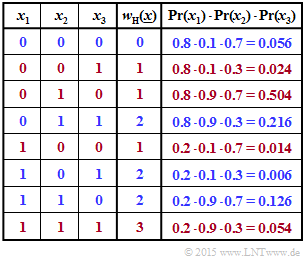
(2) In the second table, the four combinations with an even number of ones are marked in blue. The probabilities of occurrence of each combination are given in the last column. Thus, the result is:
- $$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] = 0.056 + 0.216 + 0.006 + 0.126 \hspace{0.15cm} \underline{= 0.404} \hspace{0.05cm}.$$
The red rows provide the complementary event:
- $$ {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}\right] = 0.024 + 0.504 + 0.014 + 0.054= 0.596 \hspace{0.05cm}.$$
The Gallager's equation again gives the exact same result, although it should be noted that this equation is valid for all $n$ and all arbitrary probabilities:
- $${\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \prod\limits_{i =1}^{3} \hspace{0.25cm}(1-2\cdot p_i) $$
- $$\Rightarrow\hspace{0.3cm}{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot (+0.6) \cdot (-0.8) \cdot (+0.4) = 0.404 \hspace{0.05cm}.$$
(3) According to the specification page applies:
- $$\pi = \prod\limits_{i =1}^{4} \hspace{0.25cm}(1-2\cdot p_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (1 - 2 \cdot 0.2) \cdot (1 - 2 \cdot 0.9) \cdot (1 - 2 \cdot 0.3) \cdot (1 - 2 \cdot 0.6) $$
- $$\Rightarrow\hspace{0.3cm}\pi = \prod\limits_{i =1}^{4} \hspace{0.25cm}(1-2\cdot p_i) \hspace{-0.15cm} \ = \ \hspace{-0.15cm}(+0.6) \cdot (-0.8) \cdot (+0.4) \cdot (-0.2) = 0.0384 \hspace{0.05cm}.$$
From this can be calculated:
- $${\rm Pr}({\rm blue}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 + 0.5 \cdot \pi = 0.5 + 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.5192}\hspace{0.05cm},$$
- $${\rm Pr}({\rm red}) = {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}\right] \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 0.5 - 0.5 \cdot \pi = 0.5 - 0.5 \cdot 0.0384\hspace{0.15cm} \underline{= 0.4808}\hspace{0.05cm}. $$
If you add up the blue and red probabilities on the information page, you get exactly the values calculated here.
For the quotient we get:
- $$Q = \frac{{\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} even}\right]} { {\rm Pr} \left [w_{\rm H}(\underline{x})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd}\right]} = \frac{0.5192}{0.4808}\hspace{0.15cm} \underline{= 1.0799} \hspace{0.05cm}. $$
(4) For the single parity–check code, the extrinsic $L$ value with respect to the $i$th bit was specified as follows:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} even} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{{\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm is \hspace{0.15cm} odd} \hspace{0.05cm} | \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm},$$
or:
- $$L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{1+\prod_{j \ne i} \hspace{0.25cm}(1-2\cdot p_j)}{1-\prod_{j \ne i} \hspace{0.25cm}(1-2\cdot p_j)} \hspace{0.05cm}.$$
At $\text{SPC (5, 4, 2}$) ⇒ $n = 5$, this product for $i = 5$ results from the following four factors:
- $$\pi = \prod\limits_{j = 1, \hspace{0.05cm}2, \hspace{0.05cm}3, \hspace{0.05cm}4} \hspace{0.05cm}(1-2\cdot p_j) = (1-2\cdot p_1) \cdot (1-2\cdot p_2) \cdot (1-2\cdot p_3) \cdot (1-2\cdot p_4) \hspace{0.05cm}.$$
The comparison with the subtask (3) shows that $L_{\rm E}(i = 5) = \ln {Q} = \ln {(1.0799)} \ \underline{\approx 0.077}$.
(5) Correct is proposed solution 3 because the result for $L_{\rm E}(i = 5)$ is independent of $p_5$.